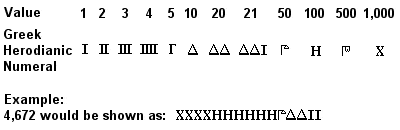
Starořecké herodovské číslovky
Když řecká říše začala rozšiřovat svou sféru vlivu do Malé Asie, Mezopotámii a dále, byli Řekové dostatečně chytří na to, aby si osvojili a přizpůsobili užitečné prvky ze společností, které si podmanili. To platilo o jejich matematice stejně jako o čemkoli jiném a přejímali prvky matematiky od Babyloňanů i Egypťanů. Brzy však začali přinášet důležité vlastní příspěvky a poprvé můžeme uznat přínos jednotlivců. V helénistickém období Řekové předsedali jedné z nejdramatičtějších a nejdůležitějších revolucí v matematickém myšlení všech dob.
Attické nebo herodovské číslice
Soustava starořeckých číslic, známá jako attické nebo herodovské číslice, byla plně vyvinuta kolem roku 450 př. n. l. a pravidelně se používala pravděpodobně již v 7. století př. n. l.. Jednalo se o systém se základem 10 podobný dřívějšímu egyptskému (a ještě podobnější pozdějšímu římskému), přičemž symboly pro 1, 5, 10, 50, 100, 500 a 1 000 se opakovaly tolikrát, kolikrát bylo třeba k vyjádření požadovaného čísla. Sčítání se provádělo odděleným sčítáním symbolů (1, 10, 100 atd.) v číslech, která se měla sčítat, a násobení byl pracný proces založený na postupném zdvojnásobování (dělení bylo založeno na obráceném postupu).
Thalesova intercepční věta
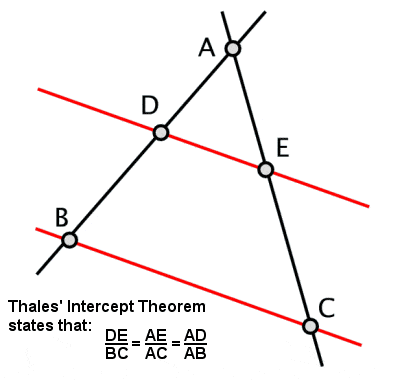
Thalesova intercepční věta
Většina řecké matematiky však byla založena na geometrii. Thalés, jeden ze sedmi mudrců starověkého Řecka, který žil na jónském pobřeží Malé Asie v první polovině 6. století př. n. l., je obvykle považován za prvního, kdo stanovil zásady abstraktního rozvoje geometrie, ačkoli to, co o jeho práci víme (například o podobných a pravoúhlých trojúhelnících), se dnes zdá být zcela elementární.
Thales stanovil to, co se stalo známým jako Thalésova věta, podle níž je-li trojúhelník nakreslen uvnitř kružnice s delší stranou jako průmětem kružnice, pak protilehlý úhel bude vždy úhlem pravým (stejně jako některé další související vlastnosti z toho odvozené). Připisuje se mu také další věta, známá také jako Thalésova věta nebo věta o průsečíku, o poměrech úseček, které vzniknou, jsou-li dvě protínající se přímky protnuty dvojicí rovnoběžek (a tím i o poměrech stran podobných trojúhelníků).
Do jisté míry se však legenda o matematikovi Pythagorovi ze Samu z 6. století př. n. l. stala synonymem zrodu řecké matematiky. Předpokládá se totiž, že právě on je autorem obou slov „filosofie“ („láska k moudrosti“) a „matematika“ („to, co je učenlivé“). Pythagoras si pravděpodobně jako první uvědomil, že lze vytvořit úplný matematický systém, v němž geometrické prvky odpovídají číslům. Pythagorova věta (neboli Pythagorova věta) je jednou z nejznámějších matematických vět. Jak ale uvidíme, zůstává kontroverzní postavou a řecká matematika se v žádném případě neomezovala na jednoho muže.
Tři geometrické problémy
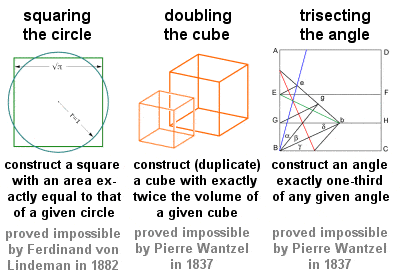
Tři klasické problémy
Zejména tři geometrické problémy, které se často označují jako tři klasické problémy a které mají být všechny vyřešeny čistě geometrickými prostředky pouze pomocí pravítka a kružítka, pocházejí z počátků řecké geometrie: „kvadratura kruhu“, „zdvojení krychle“ a „trisekce úhlu“. Tyto nesmiřitelné problémy měly hluboký vliv na budoucí geometrii a vedly k mnoha plodným objevům, i když jejich skutečné řešení (nebo, jak se ukázalo, důkazy jejich nemožnosti) muselo počkat až do 19. století.
Hippokrates z Chiosu (nezaměňovat s velkým řeckým lékařem Hippokratem z Kósu. Podrobný životopis zde.) byl jedním z takových řeckých matematiků, který se těmto problémům věnoval v 5. století př. n. l. (jeho příspěvek k problému „kvadratury kruhu“ je znám jako Hippokratova Luna). Jeho vlivná kniha „Elementy“ z doby kolem roku 440 př. n. l. byla první kompilací prvků geometrie a jeho dílo bylo důležitým zdrojem pro pozdější Euklidovo dílo.
Zenův paradox o Achillovi a želvě
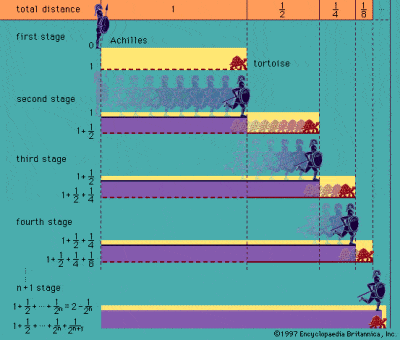
Zenův paradox o Achillovi a želvě
Byli to Řekové, kteří se poprvé potýkali s myšlenkou nekonečna, jak je popsána ve známých paradoxech připisovaných filosofovi Zenonovi z Eleje v 5. století př. n. l.. Nejznámějším z jeho paradoxů je paradox Achilles a želva, který popisuje teoretický závod mezi Achillem a želvou. Achilles dává mnohem pomalejší želvě náskok, ale než Achilles dosáhne želvího výchozího bodu, želva už je napřed. Než Achilles dosáhne tohoto bodu, želva už je zase dál atd. atd., takže rychlý Achilles v zásadě nikdy nemůže pomalou želvu dohonit.
Paradoxy, jako je tento a Zenonův tzv. dichotomický paradox, jsou založeny na nekonečné dělitelnosti prostoru a času a spočívají na myšlence, že polovina plus čtvrtina plus osmina plus šestnáctina atd. atd. do nekonečna se nikdy nebudou zcela rovnat celku. Paradox však vychází z mylného předpokladu, že není možné dokončit nekonečný počet diskrétních čárek v konečném čase, ačkoli je nesmírně obtížné tento omyl definitivně dokázat. Starověký Řek Aristoteles byl prvním z mnoha, kdo se pokusil paradoxy vyvrátit, zejména proto, že byl pevně přesvědčen, že nekonečno může být vždy pouze potenciální, a nikoli skutečné.
Demokritos, který se nejvíce proslavil svými prozíravými myšlenkami o tom, že veškerá hmota se skládá z drobných atomů, byl v 5. – 4. století př. n. l. také průkopníkem matematiky a geometrie a vytvořil díla s názvy jako „O číslech“, „O geometrii“, „O tangenciálách“, „O mapování“ a „O iracionálech“, i když se tato díla nedochovala. Víme, že byl jedním z prvních, kdo si všiml, že kužel (nebo jehlan) má o třetinu větší objem než válec (nebo hranol) se stejnou základnou a výškou, a je pravděpodobně prvním, kdo se vážně zabýval rozdělením objektů na nekonečný počet průřezů.
Je však jisté, že zejména Pythagoras výrazně ovlivnil ty, kteří přišli po něm, včetně Platóna, který v roce 387 př. n. l. založil v Athénách svou slavnou Akademii, a jeho chráněnce Aristotela, jehož dílo o logice bylo více než dva tisíce let považováno za konečné. Platón jako matematik je nejznámější pro svůj popis pěti platónských těles, ale hodnotu jeho díla jako učitele a popularizátora matematiky nelze přeceňovat.
Platónovu žákovi Eudoxovi z Knidu se obvykle připisuje první zavedení „metody vyčerpání“ (později rozvinuté Archimédem), rané metody integrace pomocí postupných aproximací, kterou použil pro výpočet objemu jehlanu a kužele. Vypracoval také obecnou teorii úměrnosti, která se vztahovala na nesouměřitelné (iracionální) veličiny, jež nelze vyjádřit jako poměr dvou celých čísel, i na souměřitelné (racionální) veličiny, čímž rozšířil Pythagorovy neúplné myšlenky.
Možná nejdůležitějším jednotlivým přínosem Řeků – a v tomto ohledu měli vliv Pythagoras, Platón i Aristoteles – však byla myšlenka důkazu a deduktivní metoda, kdy se pomocí logických kroků dokazují nebo vyvracejí tvrzení z výchozích předpokládaných axiomů. Starší kultury, jako například Egypťané a Babyloňané, se spoléhaly na induktivní uvažování, tj. na používání opakovaných pozorování ke stanovení pravidel. Právě toto pojetí důkazů dává matematice sílu a zajišťuje, že prokázané teorie jsou dnes stejně pravdivé jako před dvěma tisíci lety, a položilo základy systematického přístupu k matematice Euklida a těch, kteří přišli po něm.
| << Zpět k egyptské matematice | Především k Pythagorovi >> |
.