Úvod
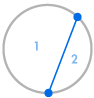
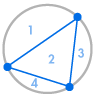
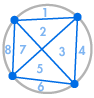
Představte si, že na obvod kruhu umístíme několik bodů a každý bod navzájem spojíme. Tím rozdělíme kružnici na mnoho různých oblastí a v každém případě můžeme spočítat počet oblastí. Následující grafy ukazují, kolik oblastí existuje pro několik různých počtů bodů na obvodu. Musíme dbát na to, aby se v každém průsečíku uvnitř kružnice setkávaly pouze dvě přímky, nikoli tři nebo více.
 |
 |
 |
 |
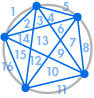 |
| 1 oblast | 2 regiony | 4 regiony | 8 regionů | 16 regionů |
Můžeme okamžitě vidět vzorec: To znamená, že při 6 bodech na obvodu by bylo 32 regionů a při 7 bodech 64 regionů.
Můžeme se rozhodnout, že jsme s tímto výsledkem spokojeni. Počet regionů je vždy dvojnásobek předchozího – koneckonců to fungovalo pro prvních pět případů. Nebo se můžeme rozhodnout, že bychom pro jistotu měli zkontrolovat ještě několik dalších:
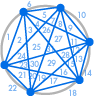 |
 |
| 31 regionů, nikoliv 32 | 57 regionů, nikoliv 64 |
Naneštěstí se něco nepovedlo: 31 může vypadat jako chyba v počítání, ale 57 je mnohem méně než 64. V tomto případě bychom měli zkontrolovat ještě několik dalších regionů. Pokračuje posloupnost 99, 163, 256, …, velmi odlišná od toho, co bychom dostali při zdvojnásobení předchozího čísla.
Tento příklad ilustruje, proč v matematice nemůžete říci, že nějaké pozorování je vždy pravdivé jen proto, že funguje v několika testovaných případech. Místo toho musíte přijít s přísným logickým argumentem, který vede od výsledků, které již znáte, k něčemu novému, co chcete ukázat jako pravdivé. Takovému argumentu se říká důkaz.
Důkazy jsou tím, čím se matematika liší od všech ostatních věd, protože jakmile něco dokážeme, máme naprostou jistotu, že to je a bude vždy pravdivé. Není to jen teorie, která odpovídá našim pozorováním a v budoucnu může být nahrazena lepší teorií.
Ve výše uvedeném příkladu bychom mohli spočítat počet průsečíků uvnitř kruhu. Pečlivé přemýšlení o vztahu mezi počtem průsečíků, přímek a oblastí nás nakonec dovede k jiné rovnici pro počet oblastí, když je x = V.Axi bodů na kružnici:
Počet oblastí = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Tato rovnice funguje ve všech výše uvedených případech. Nyní bychom se ji mohli pokusit dokázat pro každou hodnotu x pomocí „indukce“, což je technika vysvětlená níže.
Tradičně se konec důkazu označuje pomocí ■ nebo □, případně zápisem QED nebo „quod erat demonstrandum“, což je latinsky „co bylo třeba ukázat“.
Výsledek nebo pozorování, o kterém si myslíme, že je pravdivé, se nazývá hypotéza nebo domněnka. Jakmile ji dokážeme, nazýváme ji Teorém. Jakmile jsme dokázali větu, můžeme ji použít k důkazu dalších, složitějších výsledků – a tak vytvářet rostoucí síť matematických vět.
Axiomy

Rafaelova aténská škola: starověcí řečtí matematici jako první přistupovali k matematice pomocí logického a axiomatického rámce.
Jednou ze zajímavých otázek je, odkud začít. Jak dokážete první větu, když ještě nic nevíte? Bohužel nelze dokázat něco pomocí ničeho. Pro začátek potřebujete alespoň několik stavebních kamenů, kterým se říká axiomy.
Matematikové předpokládají, že axiomy jsou pravdivé, aniž by je uměli dokázat. To však není tak problematické, jak by se mohlo zdát, protože axiomy jsou buď definice, nebo jasně zřejmé, a axiomů je jen velmi málo. Axiomem může být například to, že a + b = b + a pro libovolná dvě čísla a a b.
Axiomy je důležité mít správně, protože na nich stojí celá matematika. Pokud je axiomů příliš málo, lze dokázat jen velmi málo a matematika by nebyla příliš zajímavá. Pokud je axiomů příliš mnoho, můžete dokázat téměř cokoli a matematika by také nebyla zajímavá. Také nemůžete mít axiomy, které si navzájem odporují.
Matematika není o výběru správné sady axiomů, ale o tom, jak z těchto východisek vytvořit rámec. Pokud začnete s jinými axiomy, dostanete jiný druh matematiky, ale logické argumenty budou stejné. Každá oblast matematiky má svůj vlastní soubor základních axiomů.
Když matematici dokáží nějakou větu, zveřejní ji, aby si ji ostatní matematici mohli ověřit. Někdy najdou chybu v logickém argumentu a někdy se na chybu přijde až po mnoha letech. V zásadě je však vždy možné důkaz rozložit na základní axiomy.
Teorie množin a axiom volby

K formulaci důkazů je někdy nutné vrátit se k samotnému základu jazyka, ve kterém je matematika napsána: teorii množin.
Množina je soubor objektů, například čísel. Prvky množiny se obvykle zapisují do kudrnatých závorek. Můžeme najít sjednocení dvou množin (množinu prvků, které jsou v obou množinách) nebo můžeme najít průnik dvou množin (množinu prvků, které jsou v obou množinách).
Mnoho matematických problémů lze formulovat v jazyce teorie množin a k jejich důkazu potřebujeme axiomy teorie množin. V průběhu času matematici používali různé soubory axiomů, z nichž nejrozšířenější je devět Zermelo-Fraenkelových (ZF) axiomů:
AXIOM EXTENZE
Mají-li dvě množiny stejné prvky, pak jsou si rovny.
AXIOM ROZDÍLU
Z množiny, která se skládá z některých prvků, můžeme vytvořit podmnožinu.

EMPTY SET AXIOM
Existuje množina, která nemá žádné členy, zapisuje se jako {} nebo ∅.
PŘÍMÁ OSA množiny
Při zadání dvou objektů x a y můžeme vytvořit množinu {x, y}.
JEDNOTNÁ OSA množiny
Můžeme vytvořit sjednocení dvou nebo více množin.
MOCENSKÝ AXIOM množiny
Podle libovolné množiny můžeme vytvořit množinu všech podmnožin (mocninnou množinu).
AXIOM nekonečna
Existuje množina s nekonečně mnoha prvky.

AXIOM ZÁKLADU
Množiny jsou sestaveny z jednodušších množin, což znamená, že každá (neprázdná) množina má minimální člen.
AXIOM ODMĚNY
Pokud na každý prvek množiny aplikujeme funkci, odpovědí je stále množina.
Přemýšlíte-li o teorii množin, bude vám většina těchto axiomů připadat naprosto samozřejmá – a právě takové mají axiomy být. Existuje však desátý axiom, který je poněkud problematičtější:
AXIOM VÝBĚRU
Při nekonečně mnoha neprázdných množinách lze z každé z nich vybrat jeden prvek.
Na první pohled vypadá axiom výběru (AC) stejně nevinně jako ostatní výše uvedené. Použití nekonečna má však řadu nečekaných důsledků. Pomocí AC lze například dokázat, že je možné rozříznout kouli na pět částí a znovu je složit tak, aby vznikly dvě koule, z nichž každá je totožná s původní koulí. Jedná se pouze o teoretický koncept – požadované řezy jsou fraktální, což znamená, že nemohou ve skutečnosti existovat v reálném životě, a některé z kusů jsou „neměřitelné“, což znamená, že nemají definovaný objem. Ale skutečnost, že axiom volby lze použít ke konstrukci těchto nemožných řezů, je docela znepokojující.
Mezi logiky se vede vášnivá debata, zda přijmout axiom volby, nebo ne. Každý soubor axiomů tvoří malý „matematický svět“ a v různých světech mohou platit různé věty. Jde vlastně jen o to, zda jste rádi, že žijete ve světě, kde můžete z jedné koule udělat dvě…
Důkaz indukcí
Důkaz indukcí je technika, kterou lze dokázat, že určité tvrzení je pravdivé pro všechna přirozená čísla 1, 2, 3, … „Tvrzení“ je obvykle rovnice nebo vzorec, který obsahuje proměnnou n, což může být libovolné přirozené číslo. Označme výrok aplikovaný na n jako S(n). Zde jsou čtyři kroky matematické indukce:
- Nejprve dokážeme, že S(1) je pravdivý, tj. že výrok S je pravdivý pro 1.
- Nyní předpokládáme, že S(k) je pravdivý, tj. že výrok S je pravdivý pro nějaké přirozené číslo k.
- Na základě tohoto předpokladu se pokusíme odvodit, že S(k + 1) je také pravdivý. Kdykoli je tedy S pravdivé pro jedno číslo, je pravdivé i pro další číslo.
- Jelikož víme, že S(1) je pravdivé, musí být pravdivé i S(2). A proto musí být pravdivé i S(3). A proto musí být S(4) pravdivé. A tak dále:

Indukci lze přirovnat k padajícím kostkám domina: kdykoli spadne jedna kostka domina, spadne i další. První krok, důkaz, že S(1) je pravdivé, spustí nekonečnou řetězovou reakci.
První krok je často přehlížen, protože je tak jednoduchý. Ve skutečnosti je velmi důležitý a závisí na něm celý indukční řetězec – jak ukáží některé z následujících příkladů…
Cílem hry Hanojské věže je přesunout určitý počet disků z jednoho kolíku na druhý. Vždy smíte přesunout pouze jeden disk a nesmíte položit větší disk na menší. Pokuste se přesunout věž z disků z prvního kolíku na poslední kolík, a to co nejmenším počtem tahů:
Počet disků: Počítejte s počátečními tahy:
Pokud jsme pochopili pravidla hry, můžeme se pokusit najít nejmenší potřebný počet kroků při libovolném počtu disků. Hra s výše uvedenou hrou nás může vést k pozorování, že při n discích potřebujeme alespoň 2n – 1 kroků. Nazvěme toto tvrzení S(n).
S(1) je zjevně pravdivé, protože s jedním diskem potřebujete pouze jeden tah a 21 – 1 = 1.
Nyní předpokládejme, že S(k) je pravdivé, tj. že pro k disků potřebujete 2k – 1 kroků. Pak máme-li k + 1 disků:
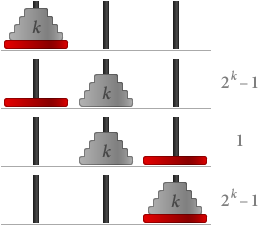
Celkem potřebujeme (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 kroků. To znamená, že S(k + 1) je také pravdivé.
Podle matematické indukce je S(n) pravdivé pro všechny hodnoty n, což znamená, že nejefektivnější způsob přesunu n = V.Hanoi disků trvá 2n – 1 = Math.pow(2,V.Hanoi)-1 tahů. ■
Použijeme indukci, abychom dokázali, že součet prvních n přirozených čísel je n (n + 1)2. Nejprve ověříme rovnici pro malé hodnoty n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Dále předpokládáme, že výsledek platí pro k, tj. že 1 + 2 + … + k = k (k + 1)2, kde k je nějaké číslo, které nespecifikujeme. Nyní
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Právě jsme dokázali, že pokud je rovnice pravdivá pro nějaké k, pak je pravdivá také pro k + 1. Matematickou indukcí je rovnice pravdivá pro všechny hodnoty n. ■
Existuje ještě jeden chytrý způsob důkazu výše uvedené rovnice, který nepoužívá indukci. Tuto metodu údajně objevil Carl Friedrich Gauss (1777 – 1855), jeden z největších matematiků v dějinách, na základní škole, když ho učitel požádal, aby sečetl všechna celá čísla od 1 do 100.
Pomocí indukce chceme dokázat, že všichni lidé mají stejnou barvu vlasů. Nechť S(n) je tvrzení, že „libovolná skupina n lidských bytostí má stejnou barvu vlasů“.
Jasně platí S(1): v libovolné skupině právě jedné mají všichni stejnou barvu vlasů.
Nyní předpokládejme S(k), že v libovolné skupině k mají všichni stejnou barvu vlasů. Nahradíme-li kteréhokoli ze skupiny někým jiným, stále tvoří celkem k, a tudíž mají stejnou barvu vlasů. To platí pro jakoukoli počáteční skupinu lidí, což znamená, že jakákoli skupina k + 1 má také stejnou barvu vlasů. Proto platí S(k + 1).
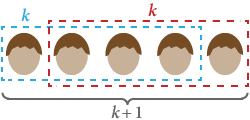
Podle matematické indukce mají všichni lidé stejnou barvu vlasů! ■
Je jasné, že ve výše uvedeném důkazu se muselo něco pokazit – ne všichni přece mají stejnou barvu vlasů. Dokážete najít chybu?“
Některé věty nelze tak docela dokázat pomocí indukce – musíme použít mírně upravenou verzi zvanou silná indukce. Místo abychom předpokládali S(k) pro důkaz S(k + 1), předpokládáme všechny S(1), S(2), … S(k) pro důkaz S(k + 1). Vše, co lze dokázat pomocí (slabé) indukce, lze zjevně dokázat i pomocí silné indukce, ale ne naopak.
Základní věta aritmetiky říká, že každé celé číslo větší než 1 je buď prvočíslo, nebo je lze zapsat jako součin prvočísel v podstatě jednoznačným způsobem.
Její části můžeme dokázat pomocí silné indukce: nechť S(n) je tvrzení, že „celé číslo n je prvočíslo nebo se dá zapsat jako součin prvočísel“. S(1) je výjimka, ale S(2) je jednoznačně pravdivé, protože 2 je prvočíslo.
Nyní předpokládejme, že S(1), S(2), …, S(k) jsou všechna pravdivá pro nějaké celé číslo k. Víme, že k + 1 je buď prvočíslo, nebo má činitele menší než k + 1. Víme, že k + 1 je prvočíslo, nebo má činitele menší než k + 1. Víme, že k + 1 je prvočíslo. Z našeho předpokladu víme, že tyto činitele lze zapsat jako součin prvočísel. Pokud tedy není prvočíslo, lze k + 1 zapsat také jako součin prvočísel. To znamená, že S(k + 1) je pravdivé.
Podle silné indukce je S(n) pravdivé pro všechna čísla n větší než 1. ■
Dokázat, že tato faktorizace prvočísel je jedinečná (pokud nepočítáme různá pořadí činitelů), vyžaduje více práce, ale není to nijak zvlášť těžké.
Ukazuje se, že princip slabé indukce a princip silné indukce jsou ekvivalentní: každý implikuje ten druhý. Oba jsou také ekvivalentní třetímu tvrzení, principu dobrého uspořádání: každá (neprázdná) množina přirozených čísel má minimální prvek, menší než všechny ostatní.
Princip dobrého uspořádání je definiční vlastností přirozených čísel. Je to jeden ze základních axiomů, který se používá k definici přirozených čísel ![]() = {1, 2, 3, …}. Tyto axiomy se nazývají Peanovy axiomy, pojmenované po italském matematikovi Guiseppe Peanovi (1858 – 1932).
= {1, 2, 3, …}. Tyto axiomy se nazývají Peanovy axiomy, pojmenované po italském matematikovi Guiseppe Peanovi (1858 – 1932).
Důkaz pomocí kontradikce
Důkaz pomocí kontradikce je další důležitou technikou důkazu. Chceme-li dokázat tvrzení S, předpokládáme, že S nebylo pravdivé. Pomocí tohoto předpokladu se pokusíme odvodit nepravdivý výsledek, například 0 = 1. Pokud byly všechny naše kroky správné a výsledek je nepravdivý, náš původní předpoklad musel být chybný. Náš původní předpoklad byl, že S není pravdivé, což znamená, že S ve skutečnosti pravdivé je.
Tuto techniku lze použít za mnoha různých okolností, například při důkazu, že √2 je iracionální, při důkazu, že reálná čísla jsou nepočitatelná, nebo při důkazu, že existuje nekonečně mnoho prvočísel.
Zde je další zábavný příklad:
K důkazu, že všechna přirozená čísla jsou „zajímavá“, můžeme použít důkaz rozporem spolu s principem dobře uspořádaných čísel.
Předpokládejme, že ne všechna přirozená čísla jsou zajímavá, a nechť S je množina nezajímavých čísel. Podle principu dobře uspořádané množiny má S nejmenší člen x, který je nejmenším nezajímavým číslem. Tato zvláštní vlastnost zjevně činí z x zvláště zajímavé číslo. To je rozpor, protože jsme předpokládali, že x je nezajímavé.
Všechna čísla jsou tedy zajímavá. ■
Gödel a nedokazatelné věty

Kurt Gödel (1906-1978)
Na počátku 20. století se matematika začala rychle rozvíjet a tisíce matematiků pracovali v nesčetných nových oblastech. David Hilbert (1862-1943) vytvořil rozsáhlý program formalizace matematiky a řešení případných nesrovnalostí v základech matematiky. Ten zahrnoval důkaz všech tvrzení pomocí souboru jednoduchých a univerzálních axiomů, důkaz, že tento soubor axiomů je konzistentní, a důkaz, že tento soubor axiomů je úplný, tj. že každé matematické tvrzení lze pomocí axiomů dokázat nebo vyvrátit.
Naneštěstí tyto plány zhatil Kurt Gödel v roce 1931. Dokázal, že v každém (dostatečně složitém) matematickém systému s určitou množinou axiomů lze najít některá tvrzení, která nelze pomocí těchto axiomů ani dokázat, ani vyvrátit. Rovněž není možné dokázat, že určitá množina axiomů je konzistentní, s použitím ničeho jiného než samotných axiomů.
Gödelův objev vychází z toho, že množinu axiomů nelze použít k tomu, aby o sobě něco řekla, například zda je konzistentní. Problémy se sebereferencí se vyskytují nejen v matematice, ale i v jazyce. Zde je paradox lháře:
„Tato věta je nepravdivá.“
Výše uvedená věta se snaží říci něco sama o sobě. Pokud je pravdivá, pak nám věta říká, že je nepravdivá. Pokud je nepravdivá, pak nám věta říká, že není nepravdivá, tj. že je pravdivá. Ve skutečnosti věta není ani pravdivá, ani nepravdivá.
Když byly Gödelovy věty poprvé publikovány, mnoho matematiků to hluboce znepokojilo. Když se pustíte do důkazu nějakého tvrzení, nevíte, zda důkaz existuje – výsledek může být pravdivý, ale nedokazatelný. Dnes víme, že neúplnost je základní součástí nejen logiky, ale i informatiky, která se opírá o stroje provádějící logické operace.
Překvapivě lze dokázat, že některá tvrzení jsou nedokazatelná. Příkladem je hypotéza o kontinuu, která se týká velikosti nekonečných množin.
Koncem svého života měl Kurt Gödel vážné psychické problémy a v roce 1978 zemřel na sebevraždu. Jeho poznatky o základech logiky byly nejhlubší od dob rozvoje důkazu u starých Řeků.