
Bertrand Russell (1872-1970) a A.N. Whitehead (1861-1947)
Bertrand Russell a Alfred North Whitehead byli britští matematici, logici a filosofové, kteří stáli v čele britské revolty proti kontinentálnímu idealismu na počátku 20. století a vzájemně významně přispěli k rozvoji matematické logiky a teorie množin.
Whitehead byl starší z nich a pocházel spíše z prostředí čisté matematiky. V 90. letech 19. století se stal Russellovým učitelem na Trinity College v Cambridgi a v prvním desetiletí 20. století pak spolupracoval se svým slavnějším bývalým žákem na jejich monumentálním díle „Principia Mathematica“. Po první světové válce, jejíž velkou část Russell kvůli svým pacifistickým aktivitám strávil ve vězení, však spolupráce ustala a Whiteheadova akademická kariéra zůstala ve stínu té Russellovy. Ve dvacátých letech emigroval do Spojených států, kde strávil zbytek života.
Russell se narodil v bohaté rodině britské aristokracie, ačkoli jeho rodiče byli na svou dobu mimořádně liberální a radikální. Jeho rodiče zemřeli, když byl Russell poměrně mladý, a vychovávala ho převážně jeho přesvědčená viktoriánská (i když poměrně pokroková) babička. Jeho dospívání bylo velmi osamělé, trpěl depresemi a později tvrdil, že jen láska k matematice ho uchránila před sebevraždou. Studoval matematiku a filozofii na Cambridgeské univerzitě pod vedením G. E. Moora a A. N. Whiteheada, kde se vypracoval v inovativního filozofa, plodného spisovatele na mnoho témat, přesvědčeného ateistu a inspirativního matematika a logika. Dnes je považován za jednoho ze zakladatelů analytické filozofie, ale psal téměř o všech významných oblastech filozofie, zejména o metafyzice, etice, epistemologii, filozofii matematiky a filozofii jazyka.
Russell byl po celý svůj dlouhý život angažovaným a vysoce postaveným politickým aktivistou. Během první i druhé světové války byl významným protiválečným aktivistou, zastával se volného obchodu a antiimperialismu a později se stal ostrým bojovníkem za jaderné odzbrojení a socialismus a proti Adolfu Hitlerovi, sovětskému totalitarismu a zapojení USA do války ve Vietnamu.
Russellův paradox
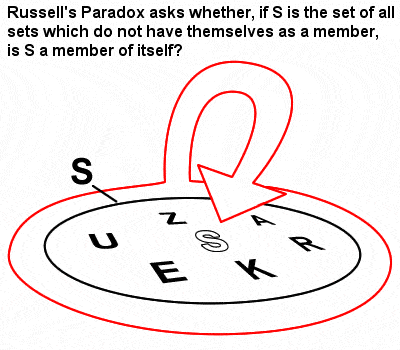
Russellův paradox
Russellova matematika byla značně ovlivněna teorií množin a logikou, kterou rozvinul Gottlob Frege v návaznosti na průkopnické rané práce Cantora o množinách. Ve svých „Principech matematiky“ z roku 1903 však identifikoval to, co se stalo známým jako Russellův paradox (množina obsahující množiny, které nejsou členy samy sebe), který ukázal, že Fregeho naivní teorie množin může ve skutečnosti vést k rozporům.
Paradox se někdy ilustruje na tomto zjednodušeném příkladu: „
Paradox jako by naznačoval, že samotným základům celé matematiky již nelze věřit a že ani v matematice nelze nikdy poznat pravdu absolutně (pozdější Gödelova a Turingova práce to jen zhorší). Russellova kritika stačila k tomu, aby otřásla Fregovou důvěrou v celou stavbu logicismu, a on byl natolik laskavý, že to otevřeně přiznal v narychlo sepsaném dodatku k II. dílu svých „Základních zákonů aritmetiky“.
Russellovým opus magnum však byla monolitická „Principia Mathematica“, vydaná ve třech svazcích v letech 1910, 1912 a 1913. Na prvním svazku se podílel Whitehead, i když pozdější dva svazky byly téměř celé Russellovým dílem. Snahou tohoto ambiciózního díla nebylo nic menšího než pokus odvodit celou matematiku z čistě logických axiomů a zároveň se vyhnout paradoxům a rozporům, které se vyskytovaly ve Fregově dřívější práci o teorii množin. Russell toho dosáhl pomocí teorie či systému „typů“, kdy je každé matematické entitě přiřazen typ v rámci hierarchie typů, takže objekty daného typu jsou sestaveny výhradně z objektů předchozích typů níže v hierarchii, což zabraňuje vzniku smyček. Každá množina prvků je tedy jiného typu než každý její prvek, takže nelze hovořit o „množině všech množin“ a podobných konstrukcích, které vedou k paradoxům.
„Principia“ však vyžadovala kromě základních axiomů teorie typů ještě tři další axiomy, které se zdály být nepravdivé jako pouhá záležitost logiky, a to „axiom nekonečna“ (který zaručuje existenci alespoň jedné nekonečné množiny, totiž množiny všech přirozených čísel), „axiom výběru“ (který zaručuje, že při dané libovolné kolekci „košů“, každý z nich obsahuje alespoň jeden objekt, je možné provést výběr právě jednoho objektu z každého koše, i když je košů nekonečně mnoho, a že neexistuje žádné „pravidlo“, který objekt z každého koše vybrat) a Russellův vlastní „axiom redukovatelnosti“ (který říká, že jakoukoli výrokovou pravdivostní funkci lze vyjádřit formálně ekvivalentní predikátovou pravdivostní funkcí).
Během zhruba deseti let, které Russell a Whitehead strávili prací na „Principiích“, byl začínán a opouštěn jeden návrh za druhým, protože Russell neustále přehodnocoval své základní premisy. Russell a jeho žena Alys se dokonce přestěhovali k Whiteheadovým, aby práci urychlili, ačkoli tím utrpělo jeho vlastní manželství, protože Russell se zamiloval do Whiteheadovy mladé ženy Evelyn. Whitehead nakonec trval na vydání díla, i když nebylo (a možná nikdy nebude) kompletní, ačkoli ho museli vydat na vlastní náklady, protože se ho nechtělo dotknout žádné komerční nakladatelství.
Principia Mathematica

Malá část dlouhého důkazu, že 1+1 = 2 v „Principia Mathematica“
Nějakou představu o rozsahu a obsáhlosti „Principia“ si lze udělat z toho, že definitivní důkaz, že 1 + 1 = 2, trvá přes 360 stran.
Dnes je všeobecně považováno za jedno z nejdůležitějších a nejzásadnějších děl v logice od dob Aristotelova „Organonu“. Zdálo se, že je pozoruhodně úspěšné a odolné ve svých ambiciózních cílech, a brzy získalo Russellovi a Whiteheadovi světovou proslulost. Ostatně teprve Gödelova věta o neúplnosti z roku 1931 nakonec ukázala, že „Principia“ nemohou být konzistentní a zároveň úplná.
Russellovi byl v roce 1949 udělen Řád za zásluhy a v následujícím roce Nobelova cena za literaturu. Jeho věhlas stále rostl, a to i mimo akademické kruhy, a v pozdějším věku se stal jakýmsi pojmem, i když převážně v důsledku svých filozofických příspěvků a svého politického a sociálního aktivismu, v němž pokračoval až do konce svého dlouhého života. Zemřel na chřipku ve svém milovaném Walesu ve vysokém věku 97 let.
| << Zpět k Hardymu a Ramanujanovi | Především k Hilbertovi >> |
.