Archimédovské spirály se často používají při analýze indukčních cívek, spirálních výměníků tepla a mikrofluidních zařízení. Dnes si ukážeme, jak sestavit Archimédovu spirálu pomocí analytických rovnic a jejich derivací k definování souboru spirálových křivek. Na základě těchto křivek pak vytvoříme 2D geometrii s určitou tloušťkou a vytlačíme ji do plné 3D geometrie.
Krátký úvod do Archimédových spirál
Spirály neboli šroubovice, v přírodě široce pozorované, se využívají v mnoha technických konstrukcích. Jako elektroinženýr můžete například vinout indukční cívky do spirál a navrhovat spirálové antény. Jako strojní inženýr můžete spirály použít při navrhování pružin, šroubovic nebo dokonce níže zvýrazněného hodinového mechanismu.

Příklad Archimédovy spirály použité v hodinovém mechanismu. Obrázek vytvořil Greubel Forsey. Pod licencí CC BY-SA 3.0, prostřednictvím Wikimedia Commons.
Nyní se zaměříme na specifický typ spirály, který se vyskytuje ve výše uvedeném mechanismu: Archimédovu spirálu. Archimédova spirála je typ spirály, která má pevnou vzdálenost mezi svými po sobě jdoucími závity. Tato vlastnost jí umožňuje široké využití při konstrukci plochých závitů a pružin.
Archimédovu spirálu můžeme v polárních souřadnicích popsat následující rovnicí:
kde a a a b jsou parametry, které určují počáteční poloměr spirály a vzdálenost mezi jejími po sobě jdoucími závity, z nichž druhý je roven 2 \pi b. Všimněte si, že Archimédova spirála se někdy označuje také jako aritmetická spirála. Tento název je odvozen od aritmetického průběhu vzdálenosti od počátku k bodu na stejném radiálu.
Návrh parametrizované geometrie archimédovské spirály
Když jsme si představili archimédovské spirály, podívejme se, jak takový návrh parametrizovat a vytvořit pro analýzu v COMSOL Multiphysics.
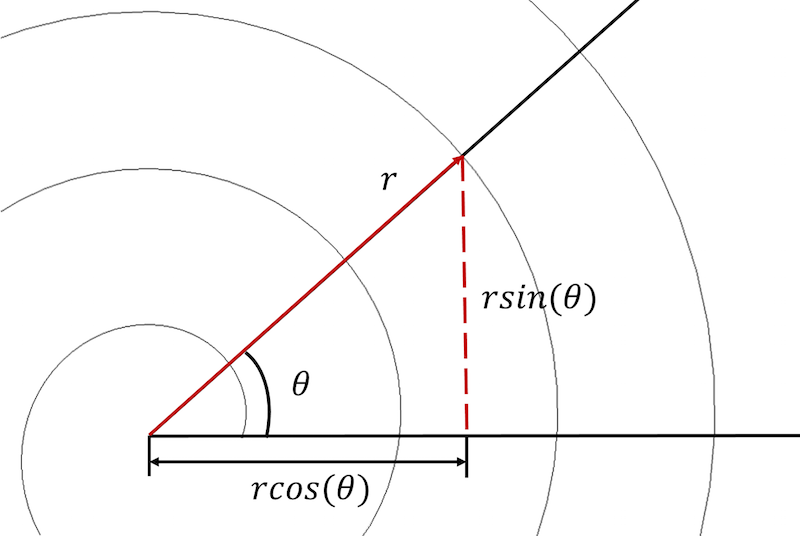
Archimédovu spirálu lze popsat v polárních i kartézských souřadnicích.
Na začátek musíme převést rovnice spirály z polárního do kartézského souřadného systému a vyjádřit každou rovnici v parametrickém tvaru:
x_{složka}=rcos(\theta) \\
y_{složka}=rsin(\theta)
\end{align*}
Tato transformace nám umožňuje přepsat rovnici Archimédovy spirály v parametrickém tvaru v kartézském souřadném systému:
x_{složka}=(a+b\theta)cos(\theta) \\
y_{složka}=(a+b\theta)sin(\theta)
\end{align*}
V systému COMSOL Multiphysics je nutné rozhodnout o souboru parametrů, které budou definovat geometrii spirály. Těmito parametry jsou počáteční poloměr spirály a_{počáteční}, konečný poloměr spirály a_{konečný} a požadovaný počet závitů n. Rychlost růstu spirály b pak lze vyjádřit takto:
Dále musíme rozhodnout o počátečním úhlu spirály theta_0 a koncovém úhlu theta_f. Začněme s hodnotami theta_0=0 a theta_f=2 \pi n. S těmito informacemi jsme schopni definovat sadu parametrů pro geometrii spirály.
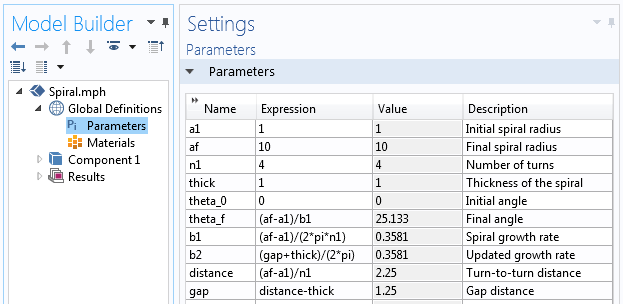
Parametry použité pro sestavení geometrie spirály.
Pro sestavení této spirály začneme s 3D komponentou a vytvoříme pracovní rovinu ve větvi Geometrie. V geometrii Work Plane pak přidáme Parametrickou křivku a pomocí výše odkazovaných parametrických rovnic s měnícím se úhlem nakreslíme 2D verzi Archimédovy spirály. Tyto rovnice můžeme zadat přímo do pole Výraz parametrické křivky, nebo můžeme každou rovnici nejprve definovat v nové analytické funkci jako:
X_{fun}=(a+bs)cos(s) \\
Y_{fun}=(a+bs)sin(s) \\
\end{align*}
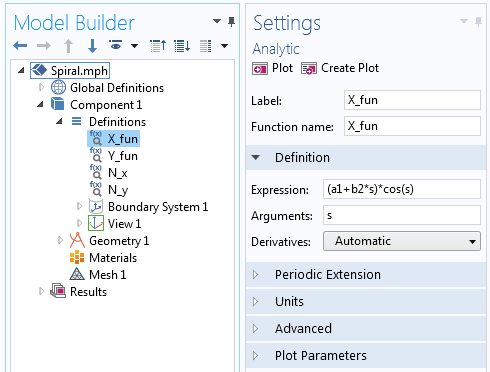
Složka X rovnice Archimédovy spirály definované v Analytické funkci.
Analytickou funkci lze použít ve výrazech pro parametrickou křivku. V této Parametrické křivce měníme parametr s od počátečního úhlu spirály, theta_0, po konečný úhel spirály, theta_f=2 \pi n.
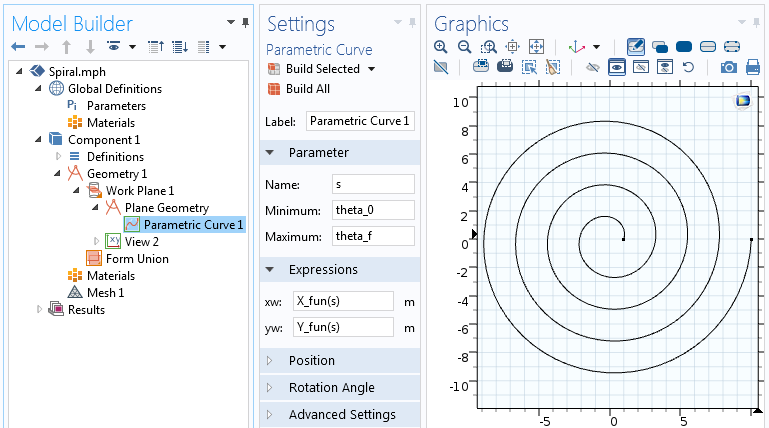
Nastavení funkce Parametrická křivka.
Rovnice parametrické spirály použité ve funkci Parametrická křivka vyústí ve spirálu reprezentovanou křivkou. Nyní na tuto geometrii navážeme a přidáme k ní tloušťku, abychom vytvořili 2D pevný objekt.
Do této chvíle byla naše spirála parametrizována v podobě počátečního poloměru a_{počáteční}, konečného poloměru a_{konečný} a požadovaného počtu závitů n. Nyní musíme do rovnice spirály zahrnout tloušťku jako další řídicí parametr.
Začněme hlavní vlastností spirály, která říká, že vzdálenost mezi závity spirály je rovna 2 \pi b. To je také ekvivalentní hodnotě \frac{a_{final}-a_{initial}}{n}. Abychom zahrnuli tloušťku, představujeme vzdálenost mezi jednotlivými po sobě jdoucími závity spirály jako součet tloušťky spirály a zbývající mezery mezi závity, thick+gap.
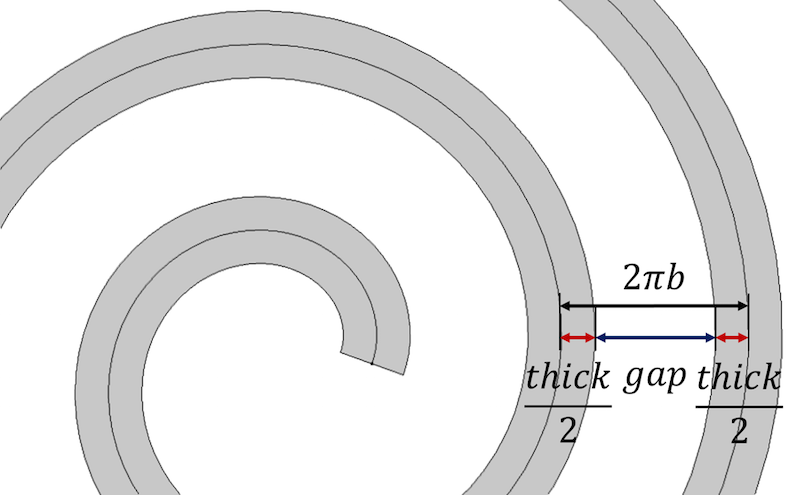
Vzdálenost mezi závity spirály je definována z hlediska parametrů tloušťky spirály a mezery.
Pro kontrolu tloušťky a získání shodné vzdálenosti mezi závity lze vzdálenost vyjádřit takto:
vzdálenost=\frac{a_{initial}-a_{final}}{n} \\
mezera=vzdálenost-tloušťka
\konec{srovnat*}
Po definování tloušťky a vyjádření mezery mezi závity v termínech tloušťky a konstantní vzdálenosti mezi osami spirály můžeme parametr růstu spirály v termínech tloušťky přepsat jako:
distance=2\pi b \\
b=\frac{gap+thick}{2\pi}
\end{align*}
Budeme také chtít vyjádřit konečný úhel spirály v termínech jejího počátečního a konečného poloměru:
\theta_{final}=2 \pi n \\
a_{final}=\text{celková vzdálenost}+a_{initial} \\
a_{final}=2 \pi bn+a_{initial} \\
n=\frac{a_{final}-a_{initial}}{2 \pi b} \\
\theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\
\theta_{final}=\frac{a_{final}-a_{initial}}{b}
\end{align*}
Chcete začít spirálu od jiného úhlu než od nuly? Pokud ano, musíte tento počáteční úhel přidat ke konečnému úhlu ve výrazu pro parametr: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0.
Duplikování stávající spirálové křivky dvakrát a umístění těchto křivek s posunem -\frac{thick}{2} a +\frac{thick}{2} vzhledem k počáteční spirálové křivce nám umožní sestavit spirálu s tloušťkou. Abychom správně umístili horní a dolní spirálu, musíme se ujistit, že posunuté spirály jsou normály k počáteční spirálové křivce. Toho dosáhneme vynásobením vzdálenosti odsazení \pm\frac{thick}{2} jednotkovým vektorem normály ke křivce spirály. Rovnice normálových vektorů ke křivce v parametrickém tvaru jsou:
kde s je parametr použitý ve funkci parametrické křivky. Abychom získali jednotkovou normálu, musíme tyto výrazy vydělit délkou normály:
Naše aktualizované parametrické rovnice pro Archimédovu spirálu s posunem o polovinu tloušťky jsou následující:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\
y_{složka}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2}
\end{align*}
Napsání těchto rovnic do výrazových polí parametrické křivky může být poměrně časově náročné. Proto zavádíme následující zápis:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
kde je každé N_x a N_y definováno pomocí analytické funkce v COMSOL Multiphysics, podobně jako jsme definovali X_{fun} a Y_{fun} pro první parametrickou křivku. V rámci funkce používáme operátor diferenciace, d(f(x),x), k provedení derivace, jak je znázorněno na následujícím snímku obrazovky.
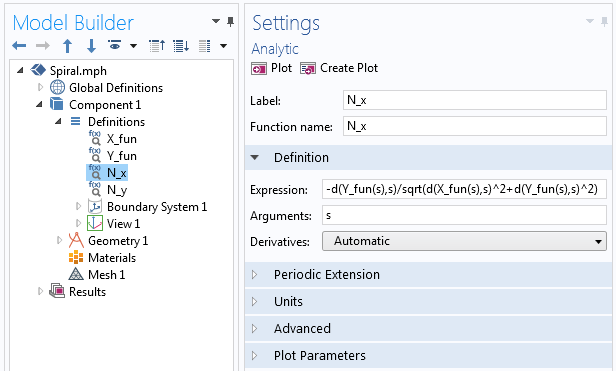
Příklady operátoru derivace použitého ve funkci Analytic.
Funkce X_{fun}, Y_{fun}, N_x a N_y pak lze použít přímo ve vyjádřeních parametrické křivky pro křivku na jedné straně:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
Funkce lze použít i pro křivku na druhé straně:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
\end{align*}
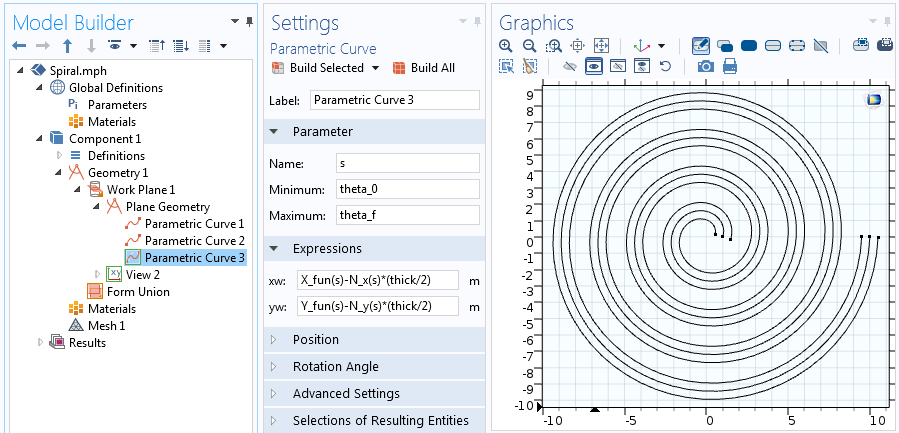
Rovnice pro druhou ze dvou posunutých parametrických křivek.
Pro spojení konců dvou křivek přidáme další dvě parametrické křivky pomocí mírné modifikace výše uvedených rovnic. Pro křivku, která spojuje střed spirály, musíme vyhodnotit X_{fun}, Y_{fun}, N_x a N_y pro počáteční hodnotu úhlu theta. Pro křivku, která se připojuje k vnější straně spirály, musíme vyhodnotit konečnou hodnotu úhlu theta. Křivka spojující střed je tedy:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2}. \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
Vnější spojovací křivka je přitom:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
V obou výše uvedených rovnicích s přechází z -1 na +1, jak ukazuje obrázek níže.
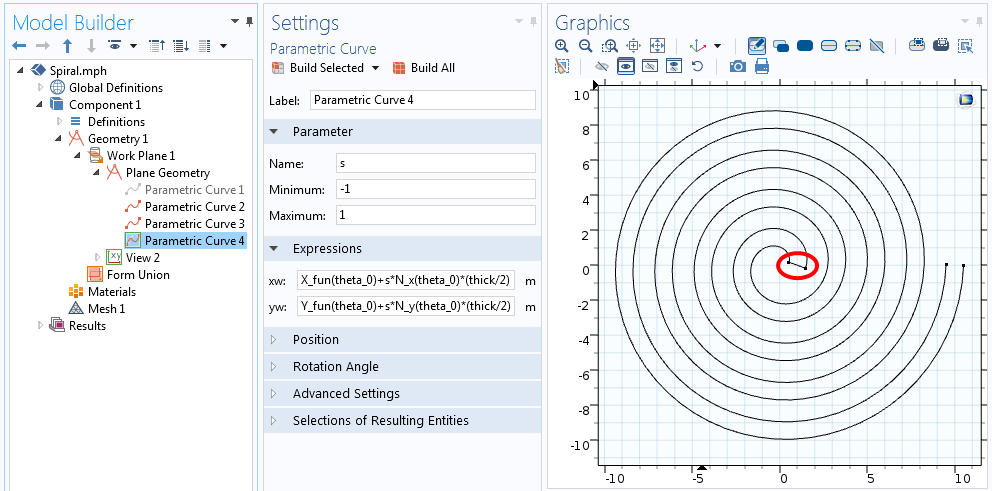
Rovnice pro křivku, která spojuje jeden konec spirály.
Máme nyní pět křivek, které definují osu spirály a všechny čtyři strany profilu. Křivku popisující středovou čáru můžeme vypnout (nebo dokonce odstranit), protože není skutečně nutná, a ponecháme pouze obrys spirály. S definovaným obrysem naší spirály můžeme pomocí operace Převést na těleso vytvořit jediný geometrický objekt. Tuto 2D spirálu lze nakonec vytlačit do 3D pomocí operace Extrude.
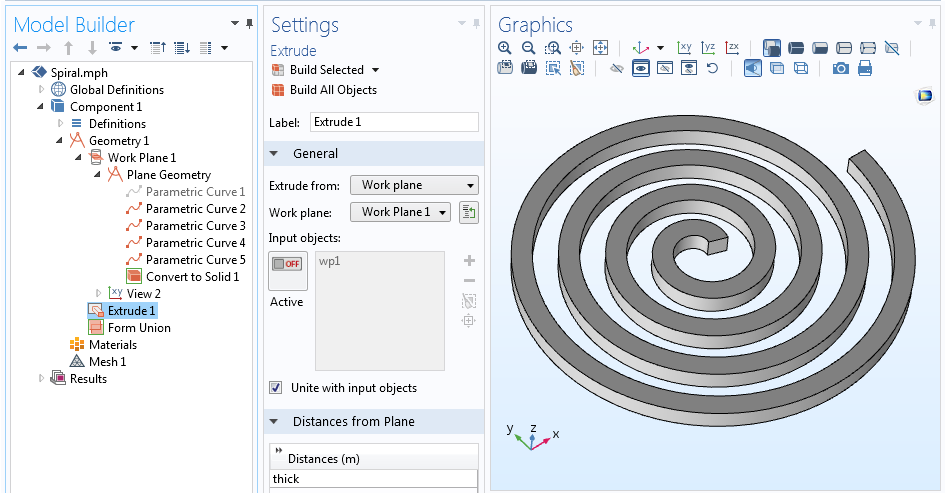
Úplná geometrická sekvence a vytlačená 3D geometrie spirály.
Závěrečné poznámky k modelování Archimédových spirál v COMSOL Multiphysics
Provedli jsme vás kroky vytvoření plně parametrizované Archimédovy spirály. S touto geometrií spirály můžete měnit libovolné parametry a experimentovat s různými konstrukcemi, nebo je dokonce použít jako parametry v optimalizační studii. Doporučujeme vám, abyste tuto techniku využili ve svých vlastních modelovacích procesech a posunuli tak analýzu svého konkrétního inženýrského návrhu založeného na spirále.