Metoda Delta-Delta Ct neboli Livakova metoda je nejpreferovanější metodou pro analýzu qPCR dat. Lze ji však použít pouze při splnění určitých kritérií, o jejichž splnění se ujistěte v poznámkách k přednášce. Pokud tomu tak není, používá se obecnější metoda zvaná Pfafflova metoda. Přečtěte si prosím doplňkové materiály k četbě, abyste získali více informací o této metodě.
Níže jsou uvedeny kroky pro Livakovu metodu:
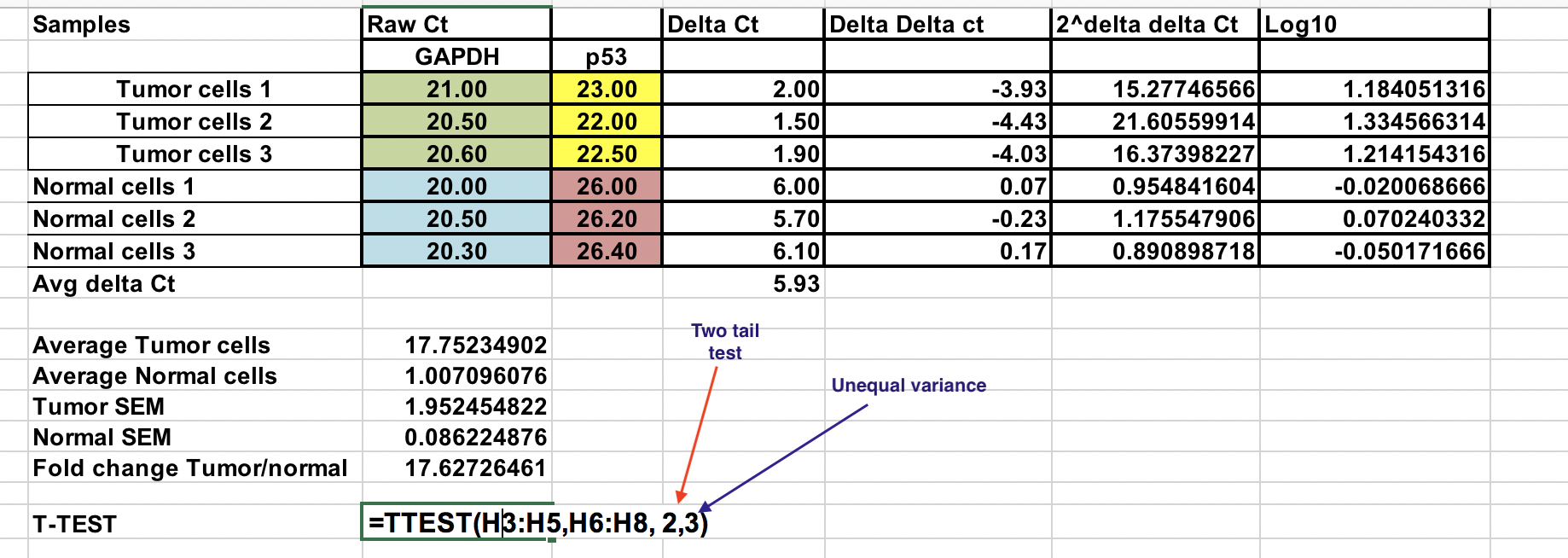
Soubor Excel se všemi výpočty je ve složce qPCR analýza na tabuli.
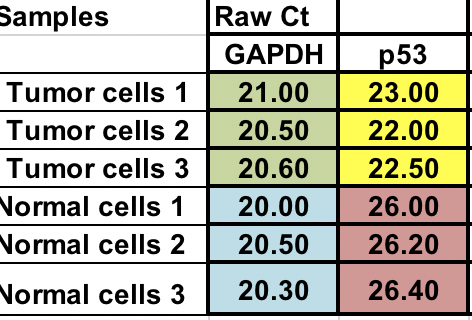
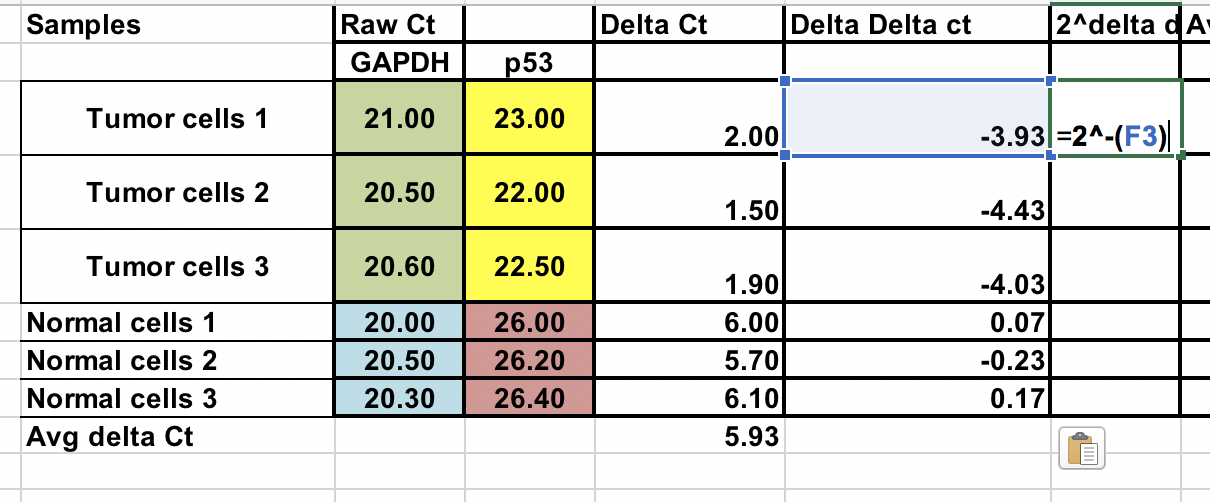
Máte surové Ct (počet cyklů, které jsou potřebné k dosažení prahové hodnoty) pro normální a nádorové buňky (3 opakování pro každou).
Normalizace¶
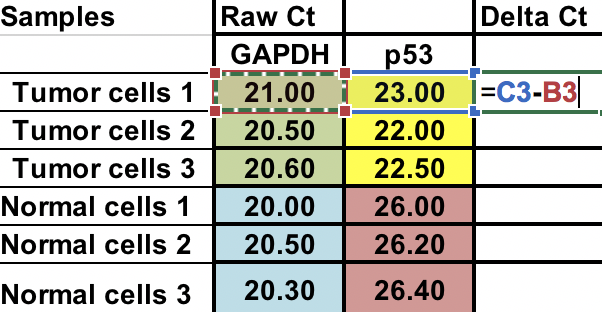
Nejprve budete muset vypočítat relativní rozdíl mezi genem zájmu (p53) a domácím genem (GAPDH).
∆Ct = Ct (gen zájmu) – Ct (housekeeping gen)
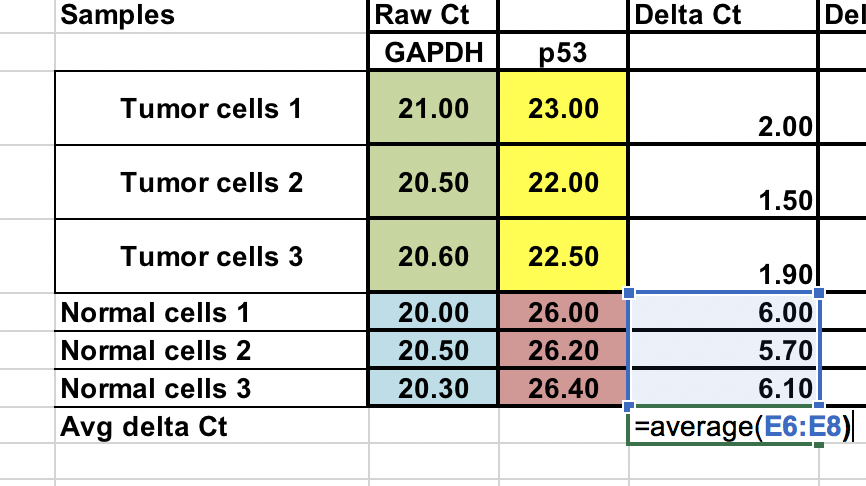
Průměr kontrolních vzorků (normální buňky)¶
Jak porovnáme náš nádor (léčbu) s kontrolou (normální buňky), musíme nejprve zprůměrovat ∆Ct pro 3 kontrolní (normální) vzorky.
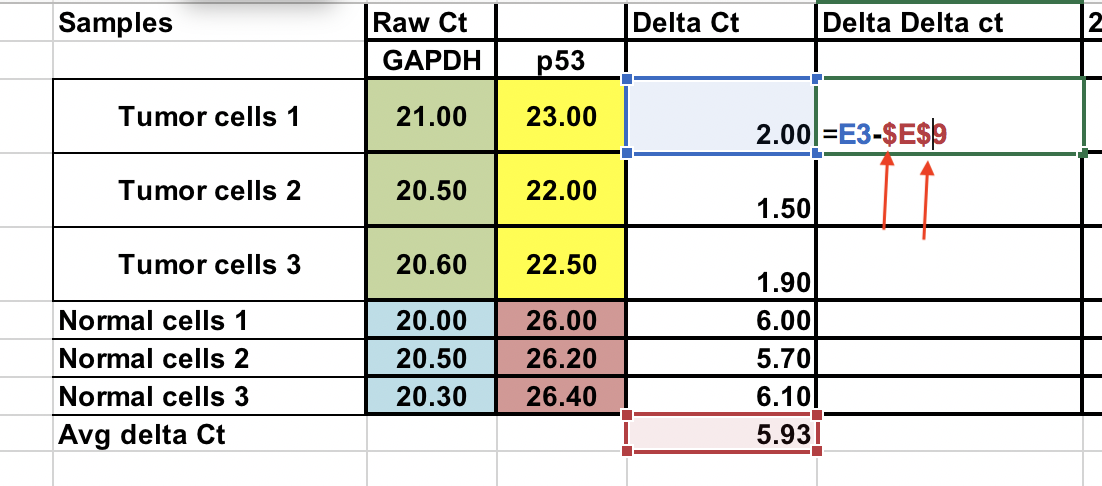
Vypočítejte ∆∆Ct vzhledem k průměru ∆Ct normálních vzorků. buněk¶
∆∆Ct = ∆Ct (nádorový vzorek) – ∆Ct (normální průměr)
Tento postup můžete provést i u normálních vzorků. Použijte znaménka $ před číslem sloupce a nezpracované písmeno (šipky) k upevnění buňky.
Násobná genová exprese pro každý vzorek¶
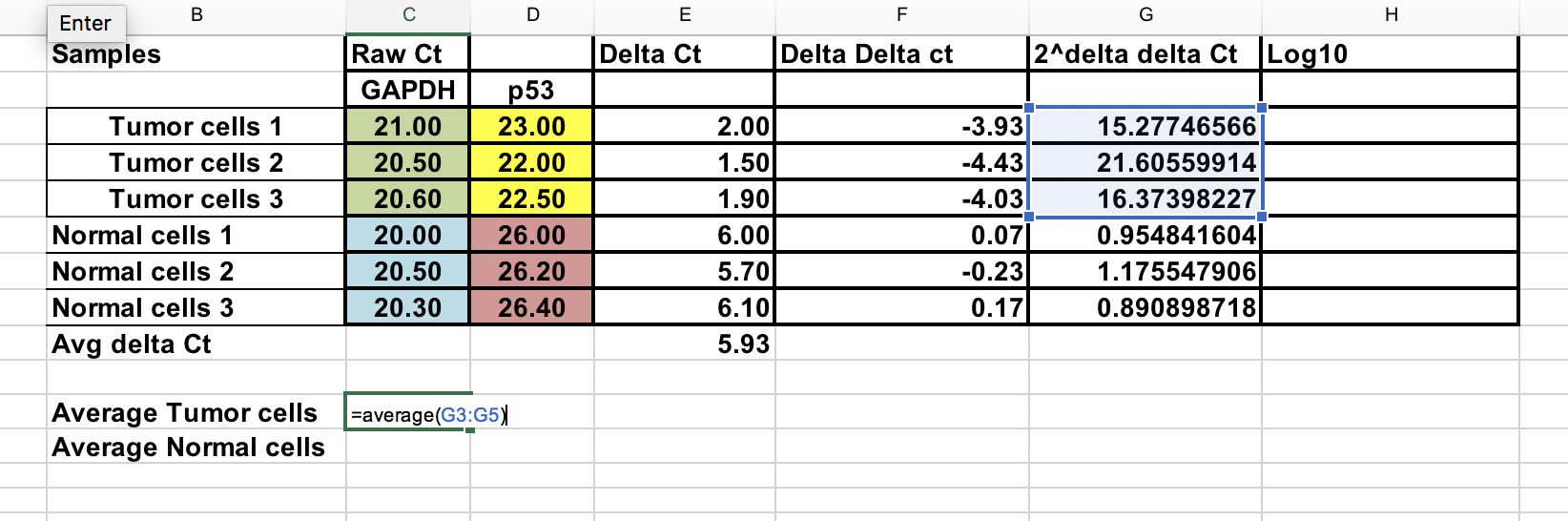
Ujistěte se, že jste zvýšili zápornou hodnotu ∆∆Ct na mocninu dvou.
Násobná genová exprese = 2^-(∆∆Ct)
Overall fold change¶
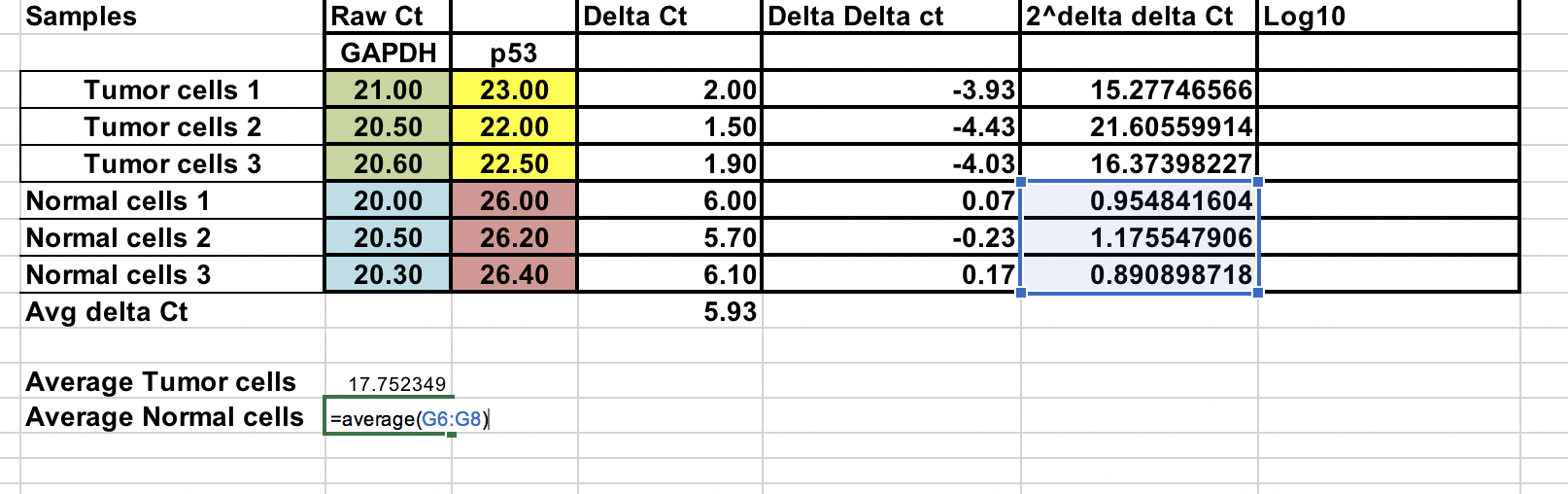
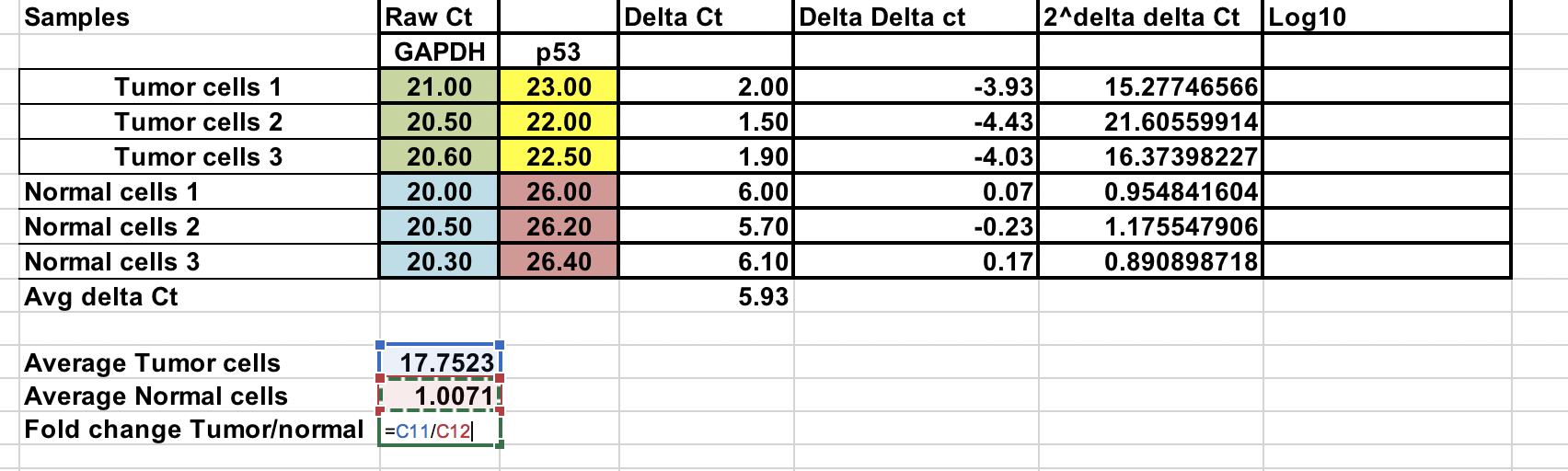
Můžete vypočítat průměrnou násobnou změnu pro nádorové i normální vzorky. Poměr mezi těmito dvěma změnami fold change mezi nádorovými a normálními vzorky.
Log transformace¶
Pro provedení parametrických statistických testů, jako je T-test, se doporučuje transformovat konečné výsledky genové exprese na logaritmické hodnoty (libovolný logaritmický základ). Tím by se rozložení dat stalo symetrickým.
Zde jsme změnili 2^-(∆∆Ct) na log 10.
T-test¶
Při používání parametrických testů je třeba být opatrný, pokud data nejsou normálně rozložena, vedlo by to k chybným závěrům.
Zvolte log 10 hodnot 2^-(∆∆Ct) pro normální a nádorové vzorky, jak je uvedeno. Použijte test dvou chvostů (číslo 2) a předpokládejte nerovnoměrný rozptyl (3).
Výsledná hodnota P je menší než 0,05, a proto zamítáme nulovou hypotézu a průměry dvou vzorků se významně liší na hladině 0,05.
.