16.3 Smíšené strategie
Cíl učení
- Jaké hry vyžadují nebo připouštějí náhodnost jako součást svého řešení?
Uvažujme opět hru s odpovídajícími penízky, jak je znázorněno na obrázku 16.13 „Matching pennies again“.
Obrázek 16.13 Matching pennies again
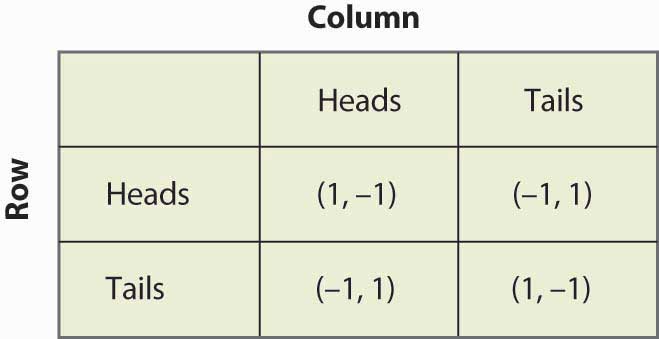
Předpokládejme, že Řádek věří, že Sloupec hraje Hlavy s pravděpodobností p. Pak pokud Řádek hraje Hlavy, Řádek dostane 1 s pravděpodobností p a -1 s pravděpodobností (1 – p), pro očekávanou hodnotu 2p – 1. V případě, že Řádek hraje Hlavy, Řádek dostane 1 s pravděpodobností (1 – p). Podobně pokud Řádek hraje Orel, dostane Řádek -1 s pravděpodobností p (když Sloupec hraje Hlavu) a 1 s pravděpodobností (1 – p), tedy očekávanou hodnotu 1 – 2p. To je shrnuto na obrázku 16.14 „Smíšená strategie v porovnávání penízků“.
Pokud 2p – 1 > 1 – 2p, pak je pro Řádek v průměru výhodnější hrát Hlavy než Orel. Podobně pokud 2p – 1 < 1 – 2p, pak je pro Row lepší hrát Orel než Hlavu. Pokud naopak 2p – 1 = 1 – 2p, pak Row dostane stejnou výhru bez ohledu na to, co Row udělá. V tomto případě by Row mohl hrát Hlavy, mohl by hrát Orel, nebo by si mohl hodit mincí a náhodně zvolit Rowovu hru.
Nashova rovnováha se smíšenou strategiíNashova rovnováha, ve které alespoň jeden hráč hraje náhodnou strategii a žádný hráč není schopen zvýšit svou očekávanou výplatu hraním alternativní strategie. involves at least one player playing a randomized strategy and no player being able to increase his or her expected payoff by playing an alternate strategy. Nashova rovnováha, v níž žádný hráč neprovádí randomizaci, se nazývá čistá strategie Nashova rovnováhaNashova rovnováha, v níž žádný hráč neprovádí randomizaci…
Obrázek 16.14 Smíšená strategie v porovnávání penízků
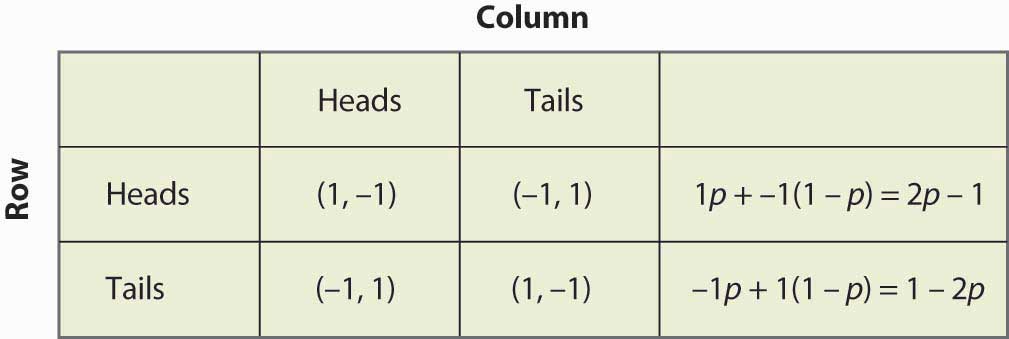
Všimněte si, že randomizace vyžaduje rovnost očekávaných výplat. Pokud má hráč randomizovat přes strategii A nebo strategii B, pak obě tyto strategie musí přinést stejnou očekávanou výplatu. Jinak by hráč preferoval jednu z nich a druhou by nehrál.
Výpočet smíšené strategie má jeden prvek, který se často jeví jako matoucí. Předpokládejme, že Řádek bude náhodný. Pak se Rowovy výhry musí rovnat pro všechny strategie, které Row hraje s kladnou pravděpodobností. Ale tato rovnost ve výplatách Řádku neurčuje pravděpodobnosti, s jakými Řádek hraje různé strategie. Místo toho tato rovnost ve výplatách Řádku určí pravděpodobnosti, s jakými Sloupec hraje různé sloupce. Důvodem je, že právě pravděpodobnosti Sloupce určují očekávané výplaty pro Řádek; pokud Řádek bude hrát náhodně, pak pravděpodobnosti Sloupce musí být takové, aby Řádek byl ochoten hrát náhodně.
Takto jsme například vypočítali výplatu Řádku ze hry Hlava, která byla 2p – 1, kde p byla pravděpodobnost, že Sloupec hraje Hlavu. Podobně výplata Řádku za to, že hraje Orel, byla 1 – 2p. Řádek je ochoten randomizovat, pokud se tyto hodnoty rovnají, což řeší p = ½.
Nyní zkusíme poněkud náročnější příklad a vrátíme se k souboji pohlaví. Obrázek 16.15 „Smíšená strategie v bitvě pohlaví“ opět ilustruje výplaty.
Obrázek 16.15 Smíšená strategie v bitvě pohlaví
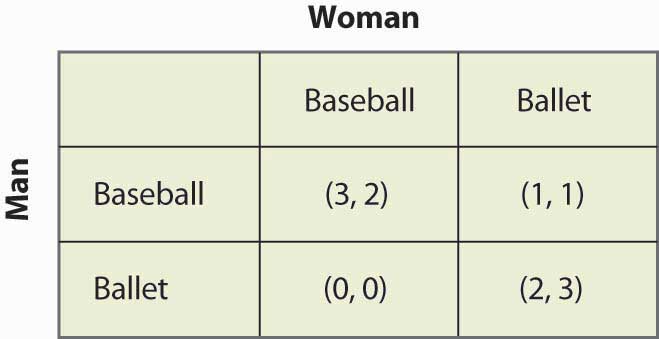
Tato hra má dvě čisté strategie Nashovy rovnováhy: (Baseball, Baseball) a (Balet, Balet). Existuje smíšená strategie? Chceme-li vypočítat smíšenou strategii, nechť Žena jde do hry Baseball s pravděpodobností p a Muž do hry Baseball s pravděpodobností q. Obrázek 16.16 „Úplný výpočet smíšené strategie“ obsahuje výpočet výplat smíšené strategie pro každého hráče.
Obrázek 16: Výplaty smíšené strategie pro každého hráče.16 Úplný výpočet smíšené strategie
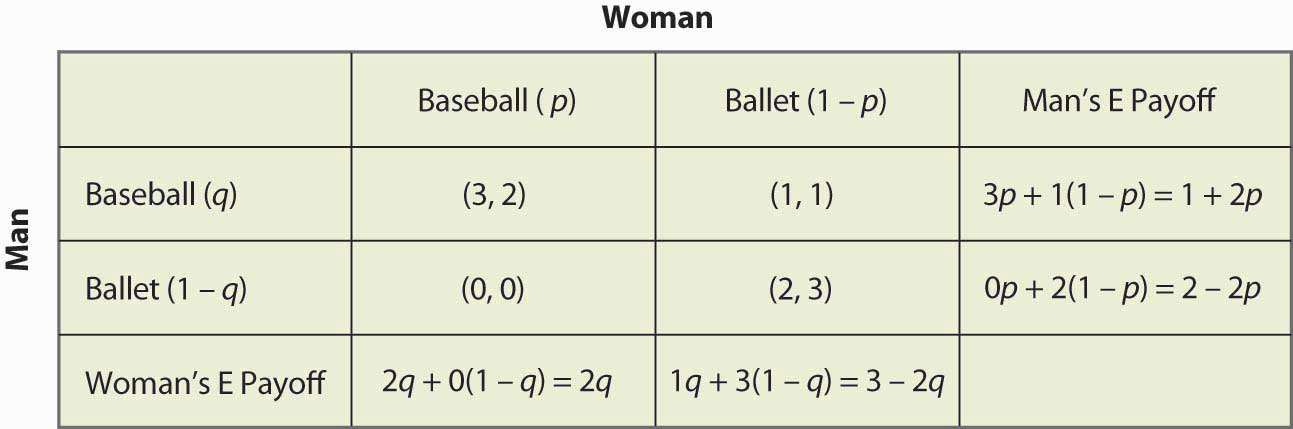
Pokud se například Muž (řádkový hráč) vydá na hru Baseball, dostane 3, když se na hru Baseball vydá Žena (pravděpodobnost p), a jinak dostane 1, přičemž očekávaná výplata je 3p + 1(1 – p) = 1 + 2p. Ostatní výpočty jsou podobné, ale určitě byste si měli projít logiku a ověřit jednotlivé výpočty.
Smíšená strategie ve hře Souboj pohlaví vyžaduje, aby obě strany randomizovaly (protože čistá strategie jedné ze stran brání randomizaci druhé strany). Mužova indiference mezi tím, zda půjde na baseball, nebo na balet, vyžaduje 1 + 2p = 2 – 2p, což dává p = ¼. To znamená, že Muž bude ochoten náhodně zvolit, na kterou akci půjde, pokud Žena půjde na balet ve ¾ případů a v opačném případě na baseball. To způsobuje, že Muž je indiferentní mezi oběma událostmi, protože dává přednost tomu, aby byl se Ženou, ale zároveň je rád na baseballovém zápase. Aby vyrovnal výhodu, kterou pro něj hra má, musí být Žena častěji na Baletu.
Podobně, aby Žena randomizovala, musí Žena získat stejnou výplatu z návštěvy Baseballového zápasu a návštěvy Baletu, což vyžaduje 2q = 3 – 2q, neboli q = ¾. To znamená, že Žena musí být častěji na Baletu než Muž. Pravděpodobnost, že Muž půjde na baseball, je tedy ¾ a na balet půjde ve ¼ případů. Jedná se o nezávislé pravděpodobnosti, takže abychom získali pravděpodobnost, že oba půjdou na Baseball, vynásobíme tyto pravděpodobnosti, čímž získáme 3/16. Obrázek 16.17 „Pravděpodobnosti smíšené strategie“ doplní pravděpodobnosti pro všechny čtyři možné výsledky.
Obrázek 16.17 Pravděpodobnosti smíšené strategie
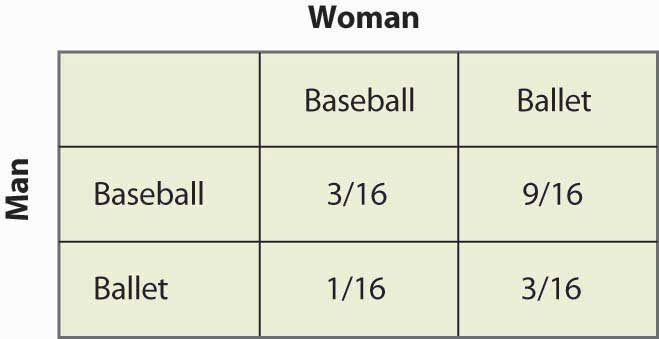
Všimněte si, že ve více než polovině případů (Baseball, Balet) je výsledkem smíšená strategie a oba lidé nejsou spolu. Tento nedostatek koordinace je obecně vlastností rovnováhy smíšené strategie. Očekávané výhry pro oba hráče lze také snadno spočítat. Výplata muže je 1 + 2p = 2 – 2p, a protože p = ¼, muž získá 1½. Podobný výpočet ukazuje, že výplata Ženy je stejná. Oba si tedy vedou hůře než při koordinaci svého méně preferovaného výsledku. Tato Nashova rovnováha se smíšenou strategií, jakkoli se může zdát nežádoucí, je však Nashovou rovnováhou v tom smyslu, že žádná ze stran nemůže zlepšit svou vlastní výplatu vzhledem k chování druhé strany.
V souboji pohlaví se Nashova rovnováha se smíšenou strategií může zdát nepravděpodobná; a mohli bychom očekávat, že pár bude koordinovat efektivněji. Ve skutečnosti by měl prostý telefonický hovor smíšenou strategii vyloučit. Uvažujme tedy jinou hru související s bitvou pohlaví, kde selhání koordinace dává větší smysl. Jedná se o hru „kuře“. V této hře jedou dva hráči proti sobě, snaží se přesvědčit toho druhého, aby ustoupil, a nakonec sjedou do příkopu. Pokud oba sjedou do příkopu, označíme výsledek za remízu a oba dostanou nulu. Pokud jeden z nich odbočí a druhý ne, řidič, který odbočí, prohraje a druhý řidič vyhraje a vítězi přidělíme jeden bod.Všimněte si, že přidání konstanty k výhrám hráče nebo vynásobení výhry hráče kladnou konstantou nemá vliv na čistou nebo smíšenou Nashovu rovnováhu. Proto můžeme vždy nechat jeden výsledek pro každého hráče nulový a druhý výsledek jedničkový. Jedinou zbývající otázkou je, co se stane, když nevyjde ani jeden, a v takovém případě dojde k havárii. V této verzi byla výhra nastavena na čtyřnásobek ztráty z odbočení, jak ukazuje obrázek 16.18 „Kuře“, ale hru můžete změnit a podívat se, co se stane.
Obrázek 16.18 Kuře
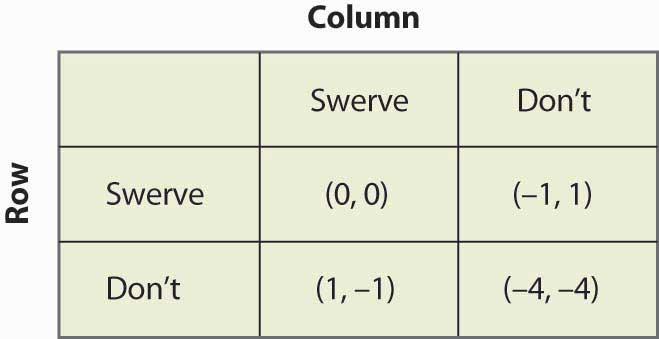
Tato hra má dvě rovnováhy čisté strategie: (Swerve, Don’t) a (Don’t, Swerve). Kromě toho má smíšenou strategii. Předpokládejme, že sloupec zatáčí s pravděpodobností p. Pak řádek získá 0p + -1(1 – p) ze zatáčení, 1p + (-4)(1 – p) z nezatáčení a řádek bude randomizovat, pokud se tyto hodnoty budou rovnat, což vyžaduje p = ¾. To znamená, že pravděpodobnost, že sloupec v rovnováze se smíšenou strategií zatočí, je ¾. Můžete si ověřit, že hráč Řádku má stejnou pravděpodobnost, když nastavíte pravděpodobnost, že Řádek vybočí, rovnou q a spočítáte očekávané výplaty Sloupce. Pravděpodobnost kolize v rovnováze smíšené strategie je tedy 1/16.
Rovnováha smíšené strategie je v této hře v jistém smyslu pravděpodobnější: Kdyby hráči již věděli, kdo ustoupí, nemuseli by vlastně hru hrát. Smyslem hry je zjistit, kdo ustoupí, což znamená, že to není předem známo. To znamená, že rovnováha se smíšenou strategií je v jistém smyslu rozumnější rovnováhou.
Obrázek 16.19 Kámen, nůžky, papír
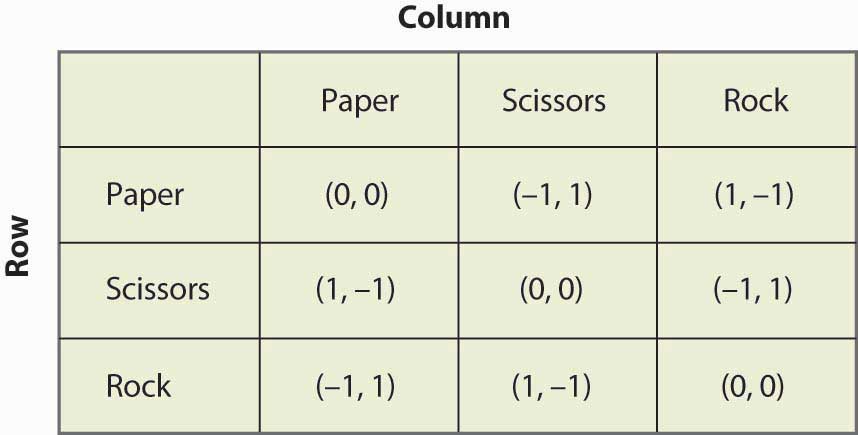
„Kámen, nůžky, papír“ je dětská hra, ve které si dvě děti pomocí rukou vybírají současně papír (ruka držená naplocho), nůžky (ruka s dvěma prsty vystrčenými tak, aby vypadaly jako nůžky) nebo kámen (ruka v pěst). Povaha výher je taková, že papír je lepší než kámen, kámen je lepší než nůžky a nůžky jsou lepší než papír. Tato hra má strukturu, která je znázorněna na obrázku 16.19 „Kámen, nůžky, papír“.
Klíčové poznatky
- Nashova rovnováha se smíšenou strategií zahrnuje alespoň jednoho hráče, který hraje náhodnou strategii, a žádný hráč není schopen zvýšit svou očekávanou výplatu hraním alternativní strategie.
- Nashova rovnováha bez náhodného výběru se nazývá Nashova rovnováha s čistou strategií.
- Předpokládá-li se, že hráč randomizuje dvě strategie, pak obě musí přinášet stejnou očekávanou výplatu.
- Hra Shodný peníz má smíšenou strategii a žádnou čistou strategii.
- Hra Souboj pohlaví má smíšenou strategii a dvě čisté strategie.
- Hra kuře je podobná hře bitva pohlaví a stejně jako ona má dvě čisté strategie a jednu smíšenou strategii.
Cvičení
- Nechť q je pravděpodobnost, že Row zahraje hlavu. Ukažte, že Sloupec je ochoten randomizovat tehdy a jen tehdy, když q = ½. (Nápověda: Nejprve vypočítejte očekávanou výplatu Sloupce, když Sloupec hraje Hlavy, a poté vypočítejte očekávanou výplatu Sloupce, když Sloupec hraje Orel. Tyto hodnoty se musí rovnat, aby Sloupek chtěl randomizovat.)
- Ukažte, že ve hře kámen, nůžky, papír neexistuje žádné čisté strategické ekvilibrium. Ukažte, že hraní všech tří akcí se stejnou pravděpodobností je rovnováha smíšené strategie.
-
Najděte všechny rovnováhy následujících her:
Obrázek 16.20
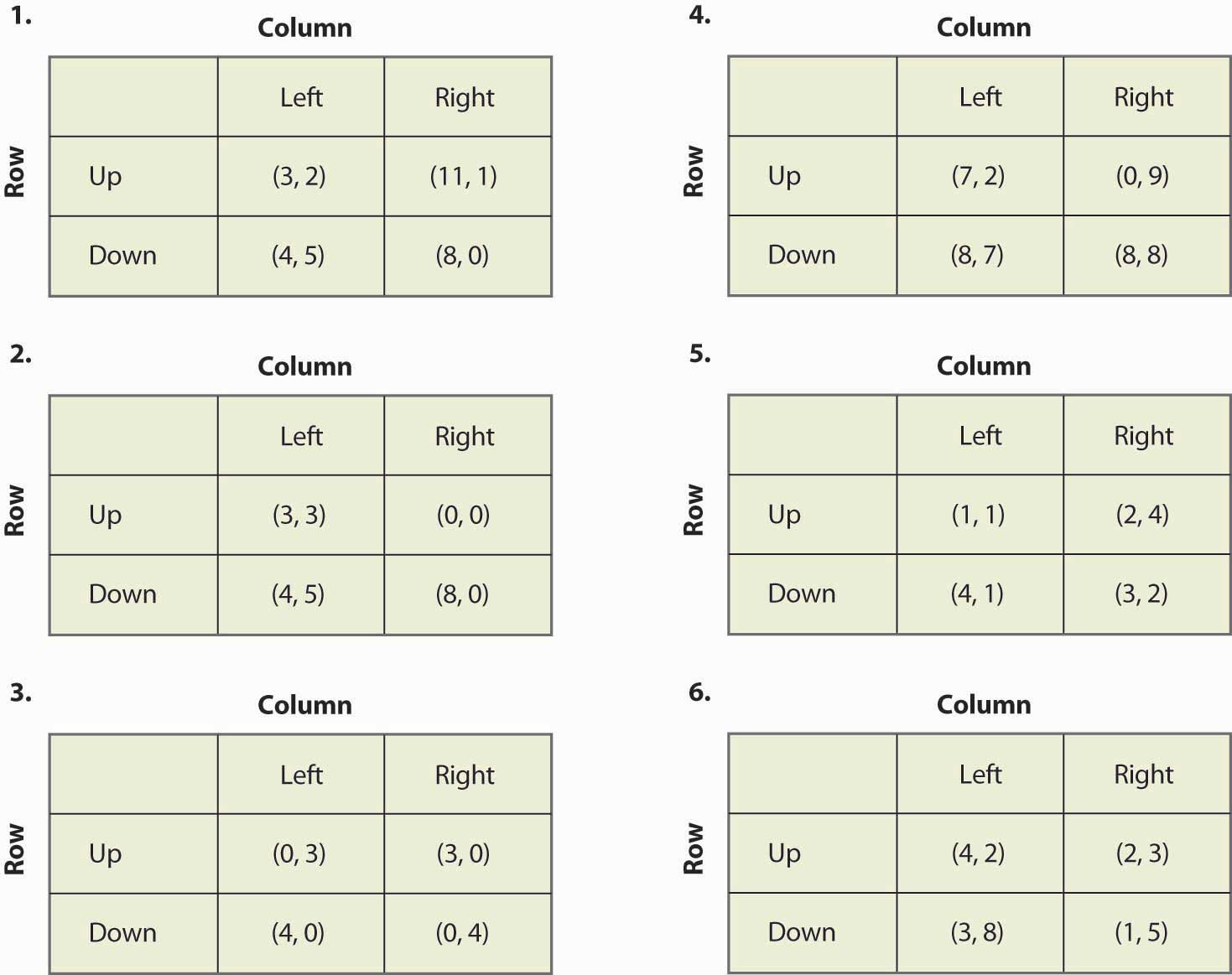
- Pokud vynásobíte výplatu hráče kladnou konstantou, rovnováhy hry se nemění. Je to pravda nebo lež a proč?