Ochrana osobních údajů & Cookies
Tato stránka používá soubory cookie. Pokračováním souhlasíte s jejich používáním. Zjistěte více, včetně toho, jak cookies ovládat.
Podívejte se na tento obrázek pravoúhlého hranolu:

Kolik vrcholů má? 8
Kolik má hran? 12
Kolik stěn? 6
Jednoduché, že?
Zkusíme další. Podívejte se na tento obrázek kužele:

Kolik má vrcholů? Počítá se vrchol nahoře?
Kolik má hran? Hmm, nejsem si jistý. Neměly by být hrany rovné?
Kolik má stěn? To je snadné! Jedna. Na spodní straně je kruhová stěna. Ale to není mnohoúhelník, takže je to pořád tvář? Aha, a jak mám nazvat tu druhou plochu na kuželu? Nemusí být stěny rovné?“
Častá otázka, kterou dostáváme od učitelů v 1., 2. a 3. třídě, souvisí s tím, jak popsat vlastnosti některých trojrozměrných těles, konkrétně válců a kuželů. Podle TEKS mají žáci popisovat trojrozměrná tělesa pomocí formálního geometrického jazyka, jako je vrchol, hrana a stěna. Potíž je v tom, že se snažíme používat jazyk, který funguje pro jednu třídu útvarů, k popisu atributů úplně jiné třídy.
Třírozměrné útvary, jako jsou hranoly a jehlany, jsou mnohostěny. „V geometrii je mnohostěn jednoduše trojrozměrné těleso, které se skládá ze souboru mnohoúhelníků, obvykle spojených na svých hranách.“ (Zdroj) Tato tělesa mají „ploché mnohoúhelníkové stěny, rovné hrany a společné rohy nebo vrcholy“. (Zdroj)
Koule, válce a kužele naopak mnohostěny nejsou. V důsledku toho nemůžeme k jejich popisu používat úplně stejný jazyk, a pokud stejný jazyk používáme, tak s tím, že definice nejsou totožné. Vezměme si například slovo vrchol.
Na pravoúhlém hranolu je vrchol ostrý bod nebo roh, kde se stýkají hrany. Obdélníkový hranol má 8 vrcholů.

Tentýž termín však lze použít i pro popis vrcholu kužele. Stejný termín, ale ne stejná definice. Jak říká Dr. Math,
skutečně ošemetné je, že „vrchol“ kužele nemá nic společného s hranami, takže potřebuje zcela novou definici; a nenapadá mě opravdu dobrá definice na základní úrovni pro to, co zjevně znamenají, což je prostě „bod“.
Když se studenti věnují pokročilejší matematice, mohou si vytvořit sofistikovanější jazyk a definice. Zatím, dokud jsou na základní škole, používáme v RRISD pro popis tohoto atributu kužele termín vrchol kužele.

Chceme-li, aby žáci popisovali a klasifikovali tento druh trojrozměrného tělesa, musíme jim k tomu poskytnout přístupný jazyk.
A co ostatní atributy kužele? Naším cílem je opět poskytnout jazyk, který je přístupný žákům základních škol a popisuje tyto atributy, přičemž si uvědomujeme, že naši žáci si později v průběhu školní docházky vytvoří formálnější porozumění. Při popisu kužele bychom řekli, že má kruhovou podstavu, tedy rovnou plochu, na které kužel spočívá. Řekneme také, že má podél podstavy zakřivený okraj a zakřivenou plochu, která se táhne od tohoto okraje až k vrcholu.
A co válec? Nyní, když máme přístupný jazyk pro popis atributů kužele, můžeme tento jazyk rozšířit na popis atributů válců.
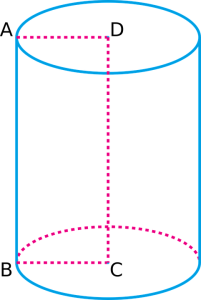
Výše uvedený válec se skládá ze dvou kruhových podstav, jedné nahoře a jedné dole. Má také dvě zakřivené hrany, jednu podél horní a jednu podél dolní části. A konečně má zakřivenou plochu, která se táhne od spodní hrany až k horní hraně.
Měl bych dodat, že kužel i válec, které jsem popsal, jsou pravý kruhový kužel a pravý válec. Stejně jako u mnohoúhelníků a mnohostěnů existuje mnoho dalších druhů příkladů těchto útvarů. Kužel nebo válec mohou být například šikmé, takže jsou šikmé.

Důležité je, aby žáci viděli různé příklady dvourozměrných a trojrozměrných útvarů. Čím více se s nimi setkávají, tím více se musí konfrontovat s jejich definicemi a terminologií, což slouží k posílení jejich porozumění atributům a tomu, jak nám pomáhají tyto útvary identifikovat a klasifikovat.
Jak to tedy vypadá v testu STAAR?
V testu STAAR zveřejněném v roce 2016 byla položena otázka, která se týkala právě tohoto tématu a posílila slovní zásobu, kterou používáme v RRISD.

Správná odpověď je F Nemají vrcholy. Pokud se podíváte na množinu B, všimnete si, že obsahuje kužel, který, jak jsme již dříve probírali, má vrchol. Kdyby Texaská vzdělávací agentura nepoužívala termín vrchol kužele, pak bychom pravděpodobně viděli, že kužel je zahrnut v množině A.
Tady je myšlenka na rozloučenou od doktora matematiky:
Jakou definici použijete, závisí na tom, co s ní budete dělat. Pokud budete pouze popisovat objekty, moje volná definice je v pořádku. Pokud se chystáte dokazovat věty zahrnující roviny a úhly, budete se chtít omezit na mnohoúhelníkovou definici, ale pak nebudete klást žádné otázky týkající se kuželoseček. Myslím, že lidé si často neuvědomují, že i když si v matematice dáváme záležet na definicích, tyto definice se liší obor od oboru, protože jsou přizpůsobeny určitému kontextu. O to se zde snažím já.
.