Indledning
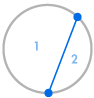
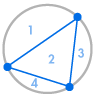
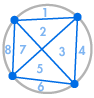
Forestil dig, at vi placerer flere punkter på omkredsen af en cirkel og forbinder alle punkterne med hinanden. Dette opdeler cirklen i mange forskellige områder, og vi kan tælle antallet af områder i hvert enkelt tilfælde. Diagrammerne nedenfor viser, hvor mange regioner der er for flere forskellige antal punkter på omkredsen. Vi skal sørge for, at kun to linjer mødes ved hvert skæringspunkt inde i cirklen, og ikke tre eller flere.
 |
 |
 |
 |
 |
 |
| 1 region | 2 regioner | 4 regioner | 8 regioner | 16 regioner |
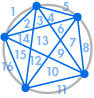
Vi kan straks se et mønster: Det betyder, at der med 6 punkter på omkredsen ville være 32 regioner, og med 7 punkter ville der være 64 regioner.
Vi kan beslutte, at vi er tilfredse med dette resultat. Antallet af regioner er altid det dobbelte af det foregående – det virkede trods alt for de første fem tilfælde. Eller vi kan beslutte, at vi skal tjekke et par stykker mere, bare for at være sikre:
 |
 |
|
| 31 regioner, ikke 32 | 57 regioner, ikke 64 |
Der er desværre gået noget galt: 31 ligner måske en regnefejl, men 57 er meget mindre end 64. Sekvensen fortsætter 99, 163, 256, …, meget forskelligt fra det, vi ville få, når vi fordobler det foregående tal.
Dette eksempel illustrerer, hvorfor man i matematik ikke bare kan sige, at en observation altid er sand, bare fordi den virker i nogle få tilfælde, man har testet. I stedet er man nødt til at komme med et stringent logisk argument, der fører fra resultater, man allerede kender, til noget nyt, som man ønsker at vise, at det er sandt. Et sådant argument kaldes et bevis.
Bevægelser er det, der adskiller matematikken fra alle andre videnskaber, for når vi først har bevist noget, er vi helt sikre på, at det er og altid vil være sandt. Det er ikke bare en teori, der passer til vores observationer, og som måske kan blive erstattet af en bedre teori i fremtiden.
I ovenstående eksempel kunne vi tælle antallet af skæringspunkter på indersiden af cirklen. Hvis vi tænker grundigt over forholdet mellem antallet af skæringspunkter, linjer og regioner, vil vi i sidste ende komme frem til en anden ligning for antallet af regioner, når der er x = V.Axi punkter på cirklen:
Antal regioner = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Denne ligning virker i alle de ovenstående tilfælde. Vi kan nu forsøge at bevise den for hver værdi af x ved hjælp af “induktion”, en teknik, der forklares nedenfor.
Traditionelt angives slutningen af et bevis ved hjælp af et ■ eller □, eller ved at skrive QED eller “quod erat demonstrandum”, som er latin for “det, der skulle vises”.
Et resultat eller en observation, som vi tror er sandt, kaldes en hypotese eller en formodning. Når vi har bevist det, kalder vi det et teorem. Når vi har bevist en sætning, kan vi bruge den til at bevise andre, mere komplicerede resultater – og dermed opbygge et voksende netværk af matematiske sætninger.
Axiomer

Raphaels skole i Athen: De gamle græske matematikere var de første til at nærme sig matematikken ved hjælp af en logisk og axiomatisk ramme.
Et interessant spørgsmål er, hvor man skal starte fra. Hvordan beviser man den første sætning, hvis man ikke ved noget endnu? Desværre kan man ikke bevise noget ved hjælp af ingenting. Du har brug for i det mindste et par byggesten at starte med, og disse kaldes aksiomer.
Matematikere antager, at aksiomer er sande uden at kunne bevise dem. Dette er dog ikke så problematisk, som det kan se ud, for aksiomer er enten definitioner eller klart indlysende, og der er kun meget få aksiomer. Et aksiom kunne f.eks. være, at a + b = b + a for to vilkårlige tal a og b.
Axiomer er vigtige at få ret, fordi hele matematikken hviler på dem. Hvis der er for få aksiomer, kan man kun bevise meget lidt, og så ville matematikken ikke være særlig interessant. Hvis der er for mange aksiomer, kan man bevise næsten hvad som helst, og så ville matematikken heller ikke være interessant. Man kan heller ikke have aksiomer, der modsiger hinanden.
Matematik handler ikke om at vælge det rigtige sæt aksiomer, men om at udvikle en ramme ud fra disse udgangspunkter. Hvis man starter med forskellige aksiomer, vil man få en anden slags matematik, men de logiske argumenter vil være de samme. Hvert område af matematikken har sit eget sæt grundlæggende aksiomer.
Når matematikere har bevist et teorem, offentliggør de det, så andre matematikere kan kontrollere det. Nogle gange finder de en fejl i det logiske argument, og nogle gange bliver en fejl først fundet mange år senere. Men i princippet er det altid muligt at bryde et bevis ned til de grundlæggende aksiomer.
Mængdeteori og valgaxiomet

For at formulere beviser er det nogle gange nødvendigt at gå tilbage til selve grundlaget for det sprog, som matematikken er skrevet i: mængdelæren.
En mængde er en samling af objekter, f.eks. tal. Elementerne i en mængde skrives normalt i krøllede parenteser. Vi kan finde foreningen af to mængder (mængden af elementer, der er i begge mængder) eller vi kan finde skæringspunktet mellem to mængder (mængden af elementer, der er i begge mængder).
Mange matematiske problemer kan formuleres i mængdelærens sprog, og for at bevise dem har vi brug for mængdelære aksiomer. I tidens løb har matematikere brugt forskellige samlinger af aksiomer, hvoraf de ni Zermelo-Fraenkel (ZF)-aksiomer er de mest accepterede:
AXIOMER OM UDVIDELSE
Hvis to mængder har de samme elementer, så er de lige store.
AXIOM FOR SEPARATION
Vi kan danne en delmængde af en mængde, som består af nogle elementer.

EMPTY SET AXIOM
Der findes en mængde uden medlemmer, der skrives som {} eller ∅.
PAIR-SET AXIOM
Givet to objekter x og y kan vi danne en mængde {x, y}.
UNION AXIOM
Vi kan danne foreningen af to eller flere mængder.
MAGTMAGTMAGTMAGT-AXIOM
Givet en hvilken som helst mængde kan vi danne mængden af alle delmængder (magtmængden).
AXIOM AF UENDELIGHEDEN
Der findes en mængde med uendeligt mange elementer.

AXIOM AF GRUNDLAG
Mængder er bygget op af enklere mængder, hvilket betyder, at hver (ikke-tom mængde) har et minimalt medlem.
AXIOM FOR FORSÆTNING
Hvis vi anvender en funktion på hvert element i en mængde, er svaret stadig en mængde.
Hvis du tænker over mængdelære, vil de fleste af disse aksiomer virke helt indlysende – og det er det, som aksiomer skal være. Der er dog et tiende aksiom, som er noget mere problematisk:
Axiom om valg
Givet uendeligt mange ikke-tomme mængder, kan man vælge et element fra hver af disse mængder.
Op det første øjekast ser aksiomet om valg (AC) lige så uskyldigt ud som de andre ovenfor. Men brugen af uendelighed har en række uventede konsekvenser. For eksempel kan man bruge AC til at bevise, at det er muligt at skære en kugle i fem stykker og samle dem igen for at lave to kugler, der hver især er identiske med den oprindelige kugle. Dette er kun et teoretisk koncept – de nødvendige opskæringer er fraktale, hvilket betyder, at de ikke kan eksistere i virkeligheden, og nogle af stykkerne er “ikke-målbare”, hvilket betyder, at de ikke har et defineret volumen. Men det faktum, at valgaxiomet kan bruges til at konstruere disse umulige snit, er ret bekymrende.
Der er en lidenskabelig debat blandt logikere, om man skal acceptere valgaxiomet eller ej. Hver samling af aksiomer danner en lille “matematisk verden”, og forskellige teoremer kan være sande i forskellige verdener. Det er egentlig bare et spørgsmål om, hvorvidt man er glad for at leve i en verden, hvor man kan lave to kugler ud af en…
Bevis ved induktion
Bevis ved induktion er en teknik, som kan bruges til at bevise, at et bestemt udsagn er sandt for alle naturlige tal 1, 2, 3, … “Udsagnet” er normalt en ligning eller formel, som indeholder en variabel n, som kan være et hvilket som helst naturligt tal. Lad os betegne udsagnet anvendt på n med S(n). Her er de fire trin i matematisk induktion:
- Først beviser vi, at S(1) er sandt, dvs. at udsagnet S er sandt for 1.
- Nu antager vi, at S(k) er sandt, dvs. at udsagnet S er sandt for et eller andet naturligt tal k.
- Ved hjælp af denne antagelse forsøger vi at udlede, at S(k + 1) også er sandt. Når S er sandt for et tal, er det altså også sandt for det næste tal.
- Da vi ved, at S(1) er sandt, må S(2) være sandt. Og derfor må S(3) også være sandt. Og derfor må S(4) være sandt. Og så videre: S må være sandt for alle tal.

Induktion kan sammenlignes med faldende dominobrikker: når en dominobrik falder, falder den næste også. Det første trin, nemlig at bevise, at S(1) er sandt, starter den uendelige kædereaktion.
Det første trin bliver ofte overset, fordi det er så simpelt. Faktisk er det meget vigtigt, og hele induktionskæden afhænger af det – som nogle af de følgende eksempler vil vise…
Spillet Tårne af Hanoi går ud på at flytte et antal skiver fra en pind til en anden. Du må kun flytte én skive ad gangen, og du må ikke lægge en større skive oven på en mindre skive. Prøv at flytte tårnet af skiver fra den første pløk til den sidste pløk med så få træk som muligt:
Antal skiver: Start forfra: Antal diske: Antal træk: 0
Når vi har forstået spillereglerne, kan vi forsøge at finde det mindste antal skridt, der er nødvendigt, givet et hvilket som helst antal skiver. Ved at lege med ovenstående spil kan vi måske konstatere, at med n skiver har man brug for mindst 2n – 1 skridt. Lad os kalde dette udsagn S(n).
S(1) er klart sandt, da man med kun én skive kun har brug for ét træk, og 21 – 1 = 1.
Lad os nu antage, at S(k) er sandt, dvs. at man har brug for 2k – 1 skridt for k skiver. Hvis vi så har k + 1 diske:
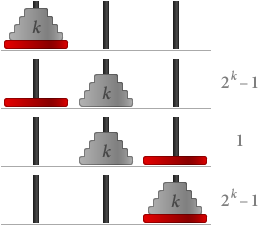
I alt har vi brug for (2k – 1) + 1 + (2k – 1) + (2k – 1) = 2(k+1) – 1 skridt. Det betyder, at S(k + 1) også er sandt.
Med matematisk induktion er S(n) sandt for alle værdier af n, hvilket betyder, at den mest effektive måde at flytte n = V.Hanoi-skiver på kræver 2n – 1 = Math.pow(2,V.Hanoi)-1 skridt. ■
Lad os bruge induktion til at bevise, at summen af de første n naturlige tal er n (n + 1)2. Vi kontrollerer først ligningen for små værdier af n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Næst antager vi, at resultatet er sandt for k, dvs. at 1 + 2 + … + k = k (k + 1)2, hvor k er et tal, vi ikke angiver. Nu
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Vi har netop bevist, at hvis ligningen er sand for et eller andet k, så er den også sand for k + 1. Ved matematisk induktion er ligningen sand for alle værdier af n. ■
Der er en anden smart måde at bevise ligningen ovenfor på, som ikke bruger induktion. Angiveligt opdagede Carl Friedrich Gauss (1777 – 1855), en af historiens største matematikere, denne metode i folkeskolen, da hans lærer bad ham lægge alle hele tal fra 1 til 100 sammen.
Ved hjælp af induktion vil vi bevise, at alle mennesker har samme hårfarve. Lad S(n) være udsagnet om, at “enhver gruppe på n mennesker har samme hårfarve”.
Det er klart, at S(1) er sandt: i enhver gruppe på blot én person har alle den samme hårfarve.
Antag nu S(k), at i enhver gruppe på k personer har alle den samme hårfarve. Hvis vi udskifter en hvilken som helst i gruppen med en anden, er de stadig i alt k og har derfor samme hårfarve. Dette gælder for enhver indledende gruppe af personer, hvilket betyder, at enhver gruppe på k + 1 også har den samme hårfarve. Derfor er S(k + 1) sandt.
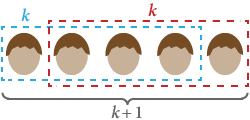
Med matematisk induktion har alle mennesker den samme hårfarve! ■
Det er klart, at der må være gået noget galt i beviset ovenfor – det er jo ikke alle, der har samme hårfarve. Kan du finde fejlen?
Nogle sætninger kan ikke helt bevises ved hjælp af induktion – vi er nødt til at bruge en lidt modificeret version kaldet stærk induktion. I stedet for at antage S(k) for at bevise S(k + 1), antager vi alle S(1), S(2), … S(k) for at bevise S(k + 1). Alt, hvad der kan bevises ved hjælp af (svag) induktion, kan tydeligvis også bevises ved hjælp af stærk induktion, men ikke omvendt.
Aritmetikkens grundsætning fastslår, at ethvert heltal større end 1 enten er et primtal, eller at det kan skrives som produktet af primtal på en i det væsentlige entydig måde.
Vi kan bevise dele af den ved hjælp af stærk induktion: Lad S(n) være udsagnet om, at “det hele tal n er et primtal eller kan skrives som et produkt af primtal”. S(1) er en undtagelse, men S(2) er klart sandt, fordi 2 er et primtal.
Lad os nu antage, at S(1), S(2), …, S(k) alle er sande, for et heltal k. Vi ved, at k + 1 enten er et primtal eller har faktorer mindre end k + 1. Ved vores antagelse ved vi, at disse faktorer kan skrives som et produkt af primtal. Medmindre det er primtal, kan k + 1 derfor også skrives som et produkt af primtal. Det betyder, at S(k + 1) er sandt.
Med stærk induktion er S(n) sandt for alle tal n større end 1. ■
At bevise, at denne primfaktorisering er entydig (medmindre man tæller forskellige rækkefølger af faktorerne) kræver mere arbejde, men er ikke særlig svært.
Det viser sig, at princippet om svag induktion og princippet om stærk induktion er ækvivalente: det ene implicerer det andet. De er også begge ækvivalente med en tredje sætning, Well-Ordering Principle: Ethvert (ikke-tomt) sæt af naturlige tal har et minimalt element, der er mindre end alle de andre.
Well-Ordering Principle er det definerende kendetegn ved de naturlige tal. Det er et af de grundlæggende aksiomer, der bruges til at definere de naturlige tal ![]() = {1, 2, 3, …}. Disse aksiomer kaldes Peanoaksiomerne, opkaldt efter den italienske matematiker Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …}. Disse aksiomer kaldes Peanoaksiomerne, opkaldt efter den italienske matematiker Guiseppe Peano (1858 – 1932).
Bevis ved modsigelse
Bevis ved modsigelse er en anden vigtig bevisteknik. Hvis vi ønsker at bevise et udsagn S, antager vi, at S ikke var sandt. Ved hjælp af denne antagelse forsøger vi at udlede et falsk resultat, som f.eks. 0 = 1. Hvis alle vores trin var korrekte, og resultatet er falsk, må vores oprindelige antagelse have været forkert. Vores oprindelige antagelse var, at S ikke er sandt, hvilket betyder, at S faktisk er sandt.
Denne teknik kan bruges under mange forskellige omstændigheder, f.eks. til at bevise, at √2 er irrationelt, til at bevise, at de reelle tal er utællelige, eller til at bevise, at der findes uendeligt mange primtal.
Her er et andet sjovt eksempel:
Vi kan bruge bevis ved modsigelse, sammen med princippet om god orden, til at bevise, at alle naturlige tal er “interessante”.
Sæt, at ikke alle naturlige tal er interessante, og lad S være mængden af ikke-interessante tal. Ved well ordering-princippet har S et mindste medlem x, som er det mindste ikke-interessante tal. Denne besynderlige egenskab gør tydeligvis x til et særligt interessant tal. Dette er en selvmodsigelse, fordi vi antog, at x var uinteressant.
Dermed er alle tal interessante. ■
Gödel og ubeviselige sætninger

Kurt Gödel (1906-1978)
I begyndelsen af det 20. århundrede begyndte matematikken at vokse hurtigt, og tusindvis af matematikere arbejdede inden for utallige nye områder. David Hilbert (1862 – 1943) iværksatte et omfattende program for at formalisere matematikken og løse eventuelle uoverensstemmelser i matematikkens grundlag. Dette omfattede bl.a. at bevise alle sætninger ved hjælp af et sæt enkle og universelle aksiomer, at bevise, at dette sæt aksiomer er konsistent, og at bevise, at dette sæt aksiomer er fuldstændigt, dvs. at ethvert matematisk udsagn kan bevises eller modbevises ved hjælp af aksiomerne.
Disse planer blev desværre ødelagt af Kurt Gödel i 1931. Han beviste, at man i ethvert (tilstrækkeligt komplekst) matematisk system med et bestemt sæt af aksiomer kan finde nogle udsagn, som hverken kan bevises eller modbevises ved hjælp af disse aksiomer. Det er heller ikke muligt at bevise, at et bestemt sæt af aksiomer er konsistent, udelukkende ved hjælp af aksiomerne selv.
Gödels opdagelse er baseret på det faktum, at et sæt af aksiomer ikke kan bruges til at sige noget om sig selv, f.eks. om det er konsistent. Problemer med selvreferencer kan ikke kun findes i matematikken, men også i sproget. Her er løgnerparadokset:
“Denne sætning er falsk.”
Sætningen ovenfor forsøger at sige noget om sig selv. Hvis den er sand, så fortæller sætningen os, at den er falsk. Hvis den er falsk, så fortæller sætningen os, at den ikke er falsk, dvs. at den er sand. I realiteten er sætningen hverken sand eller falsk.
Da Gödels sætninger blev offentliggjort første gang, var de dybt foruroligende for mange matematikere. Når man sætter sig for at bevise en observation, ved man ikke, om der findes et bevis – resultatet kan være sandt, men ikke bevisbart. I dag ved vi, at ufuldstændighed er en grundlæggende del af ikke blot logikken, men også af datalogien, som er baseret på maskiner, der udfører logiske operationer.
Overraskende nok er det muligt at bevise, at visse udsagn er ubeviselige. Et eksempel er kontinuumshypotesen, som handler om størrelsen af uendelige mængder.
Men mod slutningen af sit liv udviklede Kurt Gödel alvorlige psykiske problemer, og han døde af selvhungersnød i 1978. Hans indsigt i logikkens grundlag var den mest dybtgående siden de gamle grækeres udvikling af bevisførelse.