
Bertrand Russell (1872-1970) og A.N. Whitehead (1861-1947)
Bertrand Russell og Alfred North Whitehead var britiske matematikere, logikere og filosoffer, der stod i spidsen for det britiske oprør mod den kontinentale idealisme i begyndelsen af det 20. århundrede, og tilsammen ydede de vigtige bidrag inden for matematisk logik og mængdelære.
Whitehead var den ældste af de to og kom fra en mere ren matematisk baggrund. Han blev Russells tutor på Trinity College i Cambridge i 1890’erne og arbejdede derefter sammen med sin mere berømte tidligere elev i det første årti af det 20. århundrede på deres monumentale værk, “Principia Mathematica”. Efter Første Verdenskrig, som Russell tilbragte en stor del af i fængsel på grund af sine pacifistiske aktiviteter, blev samarbejdet dog afbrudt, og Whiteheads akademiske karriere forblev herefter i skyggen af den mere flamboyante Russell. Han emigrerede til USA i 1920’erne og tilbragte resten af sit liv der.
Russell blev født ind i en velhavende familie af det britiske aristokrati, selv om hans forældre var ekstremt liberale og radikale for tiden. Hans forældre døde, da Russell var ganske ung, og han blev i vid udstrækning opdraget af sin trofaste victorianske (om end ret progressive) bedstemoder. Hans ungdomsår var meget ensomme, og han led af depressioner og påstod senere, at det kun var hans kærlighed til matematikken, der holdt ham fra selvmord. Han studerede matematik og filosofi på Cambridge University under G.E. Moore og A.N. Whitehead, hvor han udviklede sig til en innovativ filosof, en produktiv forfatter om mange emner, en engageret ateist og en inspireret matematiker og logiker. I dag betragtes han som en af grundlæggerne af den analytiske filosofi, men han skrev om næsten alle større områder af filosofien, især metafysik, etik, epistemologi, matematikkens filosofi og sprogfilosofi.
Russell var en engageret og højt profileret politisk aktivist gennem hele sit lange liv. Han var en fremtrædende antikrigsaktivist under både Første og Anden Verdenskrig, han var fortaler for frihandel og antiimperialisme, og senere blev han en skarp forkæmper for atomnedrustning og socialisme og mod Adolf Hitler, den sovjetiske totalitarisme og USA’s engagement i Vietnamkrigen.
Russells paradoks
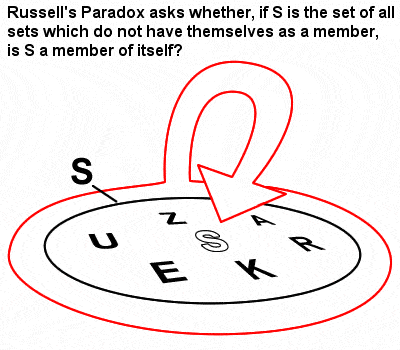
Russells paradoks
Russells matematik var stærkt påvirket af den mængdelære og logik, som Gottlob Frege havde udviklet i kølvandet på Cantors banebrydende tidlige arbejde om mængder. I sin “The Principles of Mathematics” fra 1903 identificerede han imidlertid det, der er blevet kendt som Russells paradoks (en mængde, der indeholder mængder, som ikke er medlemmer af sig selv), hvilket viste, at Freges naive mængdelære faktisk kunne føre til modsigelser.
Paradokset illustreres nogle gange med dette forsimplede eksempel: “Hvis en barber barberer alle og kun de mænd i landsbyen, der ikke barberer sig selv, barberer han så sig selv?”
Paradokset syntes at antyde, at man ikke længere kunne stole på selve grundlaget for hele matematikken, og at man selv i matematikken aldrig kunne kende sandheden absolut (Gödels og Turings senere arbejde ville kun gøre dette endnu værre). Russells kritik var nok til at rokke ved Freges tillid til hele logicismens bygningsværk, og han var nådig nok til at indrømme dette åbent i et hastigt skrevet tillæg til bind II af hans “Basic Laws of Arithmetic”.
Men Russells hovedværk var den monolitiske “Principia Mathematica”, der blev udgivet i tre bind i 1910, 1912 og 1913. Det første bind blev skrevet i samarbejde med Whitehead, selv om de to senere bind næsten udelukkende var Russells værk. Målet med dette ambitiøse værk var intet mindre end et forsøg på at udlede hele matematikken fra rent logiske aksiomer, samtidig med at man undgik de former for paradokser og modsigelser, som man fandt i Freges tidligere arbejde om mængdelære. Russell opnåede dette ved at anvende en teori eller et system af “typer”, hvor hver matematisk enhed tildeles en type inden for et hierarki af typer, således at objekter af en given type udelukkende er bygget op af objekter af forudgående typer lavere i hierarkiet, hvilket forhindrer sløjfer. Hver mængde af elementer er således af en anden type end hvert af dens elementer, således at man ikke kan tale om “mængden af alle mængder” og lignende konstruktioner, som fører til paradokser.
Derimod krævede “Principia” ud over typeteoriens grundlæggende aksiomer yderligere tre aksiomer, der tilsyneladende ikke var sande som rene logiske spørgsmål, nemlig “uendelighedsaksiomet” (som garanterer eksistensen af mindst én uendelig mængde, nemlig mængden af alle naturlige tal), “valgaxiomet” (som sikrer, at man, givet en hvilken som helst samling af “bins”, der hver indeholder mindst ét objekt, er det muligt at vælge præcis ét objekt fra hver beholder, selv om der er uendeligt mange beholdere, og at der ikke findes nogen “regel” for, hvilket objekt der skal vælges fra hver beholder) og Russells eget “reduktionsaksiom” (som fastslår, at enhver propositionel sandhedsfunktion kan udtrykkes ved en formelt ækvivalent prædikativ sandhedsfunktion).
I løbet af de ca. ti år, som Russell og Whitehead brugte på “Principia”, blev udkast efter udkast påbegyndt og opgivet, idet Russell hele tiden genovervejede sine grundlæggende forudsætninger. Russell og hans kone Alys flyttede endda ind hos Whiteheads for at fremskynde arbejdet, selv om hans eget ægteskab led under, at Russell blev forelsket i Whiteheads unge kone, Evelyn. Til sidst insisterede Whitehead på at få værket udgivet, selv om det ikke var (og måske aldrig ville blive) færdigt, selv om de var tvunget til at udgive det på egen regning, da ingen kommercielle forlag ville røre det.
Principia Mathematica

En lille del af det lange bevis for, at 1+1 =2 i “Principia Mathematica”
En vis idé om “Principia”‘s rækkevidde og omfang kan aflæses af det faktum, at det tager over 360 sider at bevise endeligt, at 1 + 1 = 2.
I dag anses det generelt for at være et af de vigtigste og mest banebrydende værker inden for logikken siden Aristoteles’ “Organon”. Den virkede bemærkelsesværdigt vellykket og modstandsdygtig i sine ambitiøse mål og skabte hurtigt verdensberømmelse for Russell og Whitehead. Faktisk var det først Gödels ufuldstændighedssætning fra 1931, der endelig viste, at “Principia” ikke kunne være både konsistent og komplet.
Russell blev tildelt fortjenstordenen i 1949 og Nobelprisen i litteratur det følgende år. Hans berømmelse fortsatte med at vokse, også uden for akademiske kredse, og han blev noget af et kendt navn senere i livet, om end i høj grad som følge af hans filosofiske bidrag og hans politiske og sociale aktivisme, som han fortsatte med indtil slutningen af sit lange liv. Han døde af influenza i sit elskede Wales i en alder af 97 år.
| << Tilbage til Hardy og Ramanujan |
Forward to Hilbert >> |