16.3 Blandede strategier
Læringsmål
- Hvilke spil kræver eller tillader randomisering som en del af deres løsning?
Lad os igen se på spillet med mønter, som er illustreret i figur 16.13 “Matching pennies again”.
Figur 16.13 Matching pennies again
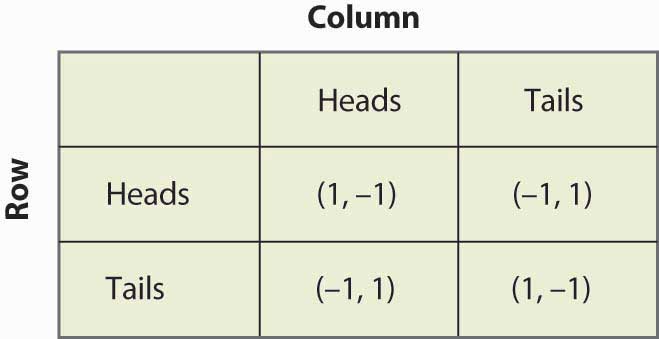
Sæt, at række tror, at kolonne spiller plat med sandsynligheden p. Hvis række spiller plat, får række 1 med sandsynligheden p og -1 med sandsynligheden (1 – p), hvilket giver en forventet værdi på 2p – 1. På samme måde, hvis Row spiller på plat, får Row -1 med sandsynlighed p (når Column spiller på plat) og 1 med sandsynlighed (1 – p), hvilket giver en forventet værdi på 1 – 2p. Dette er opsummeret i figur 16.14 “Blandet strategi i matching pennies”.
Hvis 2p – 1 > 1 – 2p, så er Row i gennemsnit bedre stillet ved at spille plat end krone. Tilsvarende gælder det, at hvis 2p – 1 < 1 – 2p, så er Row bedre stillet ved at spille plat end krone. Hvis derimod 2p – 1 = 1 – 2p, så får Row den samme gevinst, uanset hvad Row gør. I dette tilfælde kunne Row spille plat, kunne spille krone eller kunne kaste en mønt og randomisere Row’s spil.
En blandet strategi Nash-ligevægtEn Nash-ligevægt, hvor mindst én spiller spiller en randomiseret strategi, og ingen spiller er i stand til at øge sin forventede gevinst ved at spille en alternativ strategi. indebærer, at mindst én spiller spiller en randomiseret strategi, og ingen spiller er i stand til at øge sin forventede gevinst ved at spille en alternativ strategi. En Nash-ligevægt, hvor ingen spiller randomiserer, kaldes en ren strategi Nash-ligevægtEn Nash-ligevægt, hvor ingen spiller randomiserer..
Figur 16.14 Blandet strategi ved matchning af pennies
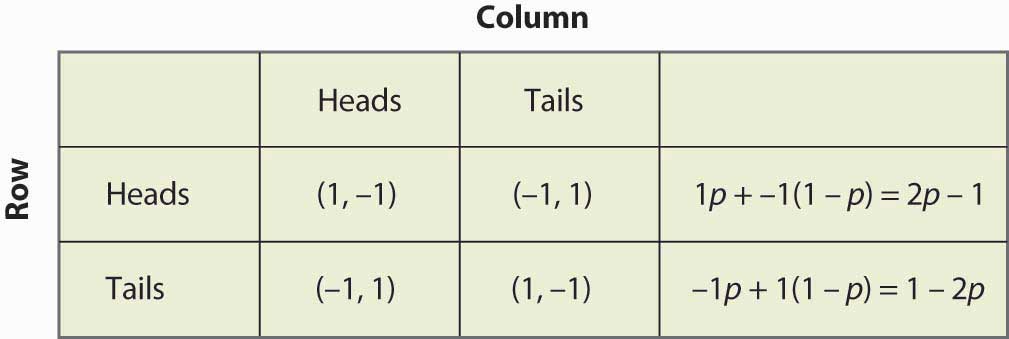
Bemærk, at randomisering kræver lighed i de forventede udbetalinger. Hvis det er meningen, at en spiller skal randomisere over strategi A eller strategi B, skal begge disse strategier give den samme forventede udbetaling. Ellers ville spilleren foretrække den ene af dem og ville ikke spille den anden.
Beregning af en blandet strategi har et element, som ofte virker forvirrende. Lad os antage, at Row vil randomisere. Så skal Row’s udbetalinger være lige store for alle strategier, som Row spiller med positiv sandsynlighed. Men denne lighed i Row’s payoffs bestemmer ikke de sandsynligheder, hvormed Row spiller de forskellige rækker. I stedet vil ligheden i Row’s payoffs bestemme de sandsynligheder, hvormed Column spiller på de forskellige kolonner. Årsagen er, at det er kolonnens sandsynligheder, der bestemmer de forventede gevinster for Row; hvis Row vil randomisere, så skal kolonnens sandsynligheder være sådan, at Row er villig til at randomisere.
Sådan beregnede vi for eksempel Row’s gevinst ved at spille på hoveder, som var 2p – 1, hvor p var sandsynligheden for, at Kolonnen spillede på hoveder. På samme måde var gevinsten for række ved at spille plat 1 – 2p. Row er villig til at randomisere, hvis disse er lige store, hvilket løser p = ½.
Nu skal vi prøve et noget mere udfordrende eksempel og gense kampen mellem kønnene. Figur 16.15 “Mixed strategy in battle of the sexes” illustrerer endnu en gang udbetalingerne.
Figur 16.15 Mixed strategy in battle of the sexes
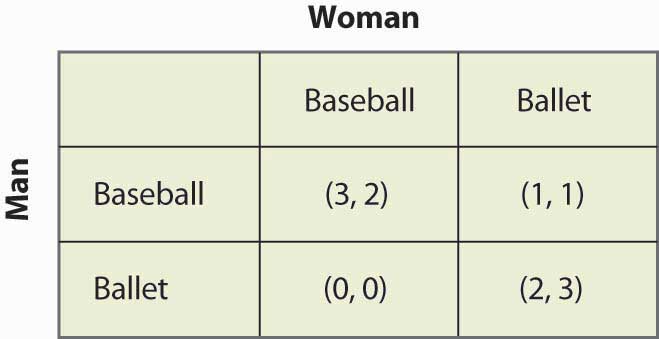
Dette spil har to Nash-ligevægte med ren strategi: (Baseball, Baseball) og (Ballet, Ballet). Er der en blandet strategi? For at beregne en blandet strategi skal man lade kvinden gå til baseballspillet med sandsynlighed p og manden gå til baseballspillet med sandsynlighed q. Figur 16.16 “Fuld beregning af den blandede strategi” indeholder beregningen af udbetalingerne for den blandede strategi for hver spiller.
Figur 16.16 Fuld beregning af den blandede strategi
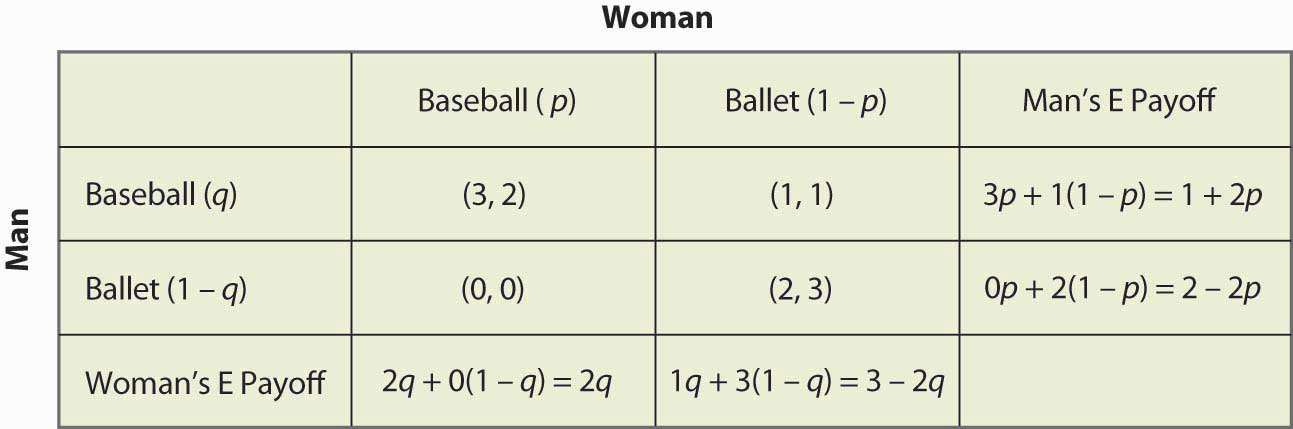
For eksempel, hvis manden (rækkens spiller) går til baseballspillet, får han 3, når kvinden går til baseballspillet (sandsynlighed p), og ellers får han 1, hvilket giver en forventet gevinst på 3p + 1(1 – p) = 1 + 2p. De andre beregninger ligner hinanden, men du bør helt sikkert gennemgå logikken og verificere hver enkelt beregning.
En blandet strategi i kampen om kønnenes kamp kræver, at begge parter randomiserer (da en ren strategi fra en af parterne forhindrer randomisering fra den anden). Mandens ligegyldighed mellem at gå til baseballspillet og til ballet kræver 1 + 2p = 2 – 2p, hvilket giver p = ¼. Det vil sige, at manden vil være villig til at vælge tilfældigt, hvilken begivenhed han deltager i, hvis kvinden går til ballet ¾ af tiden, og ellers til baseballkampen. Dette gør manden ligeglad mellem de to begivenheder, fordi han foretrækker at være sammen med kvinden, men han kan også godt lide at være til baseballkampen. For at opveje den fordel, som spillet giver ham, må kvinden være til ballet oftere.
Sådan skal kvinden, for at hun kan randomisere, få lige store gevinster ved at gå til baseballkampen og til ballet, hvilket kræver 2q = 3 – 2q, eller q = ¾. Sandsynligheden for, at manden går til baseballkampen, er således ¾, og han går til ballet ¼ af gangene. Det er uafhængige sandsynligheder, så for at få sandsynligheden for, at begge går til baseballkampen, skal vi gange sandsynlighederne, hvilket giver 3/16. Figur 16.17 “Sandsynligheder for blandet strategi” udfylder sandsynlighederne for alle fire mulige udfald.
Figur 16.17 Sandsynligheder for blandet strategi
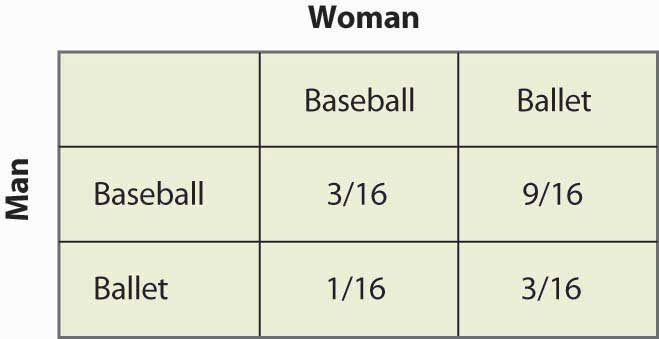
Bemærk, at mere end halvdelen af tiden (Baseball, Ballet) er udfaldet af den blandede strategi, og de to personer er ikke sammen. Denne mangel på koordinering er generelt et kendetegn ved blandede strategibalancer. De forventede udbetalinger for begge spillere kan også let beregnes. Mandens gevinst er 1 + 2p = 2 – 2p, og da p = ¼, opnår manden 1½. En lignende beregning viser, at kvindens gevinst er den samme. Begge klarer sig således dårligere end at koordinere deres mindre foretrukne udfald. Men denne Nash-ligevægt med blandet strategi, hvor uønsket den end kan virke, er en Nash-ligevægt i den forstand, at ingen af parterne kan forbedre sin egen payoff, givet den anden parts adfærd.
I kampen mellem kønnene kan den blandede Nash-ligevægt med blandet strategi virke usandsynlig; og vi kunne forvente, at parret koordinerer mere effektivt. Faktisk burde et simpelt opkald i telefonen udelukke den blandede strategi. Lad os derfor overveje et andet spil relateret til kampen mellem kønnene, hvor en manglende koordinering giver mere mening. Dette er spillet “kylling”. I dette spil kører to spillere mod hinanden og forsøger at overbevise den anden om at give efter og i sidste ende køre ud i en grøft. Hvis begge kører i grøften, kalder vi resultatet uafgjort, og begge får nul. Hvis den ene kører ud, og den anden ikke gør det, taber den chauffør, der kører ud, og den anden chauffør vinder, og vi giver vinderen et point.Bemærk, at det ikke påvirker Nash-ligevægtene – hverken den rene eller den blandede – at tilføje en konstant til en spillers gevinst eller at multiplicere denne spillers gevinst med en positiv konstant. Derfor kan vi altid lade et udfald for hver spiller være nul og et andet udfald være et. Det eneste tilbageværende spørgsmål er, hvad der sker, når ingen af dem giver udbytte, i hvilket tilfælde der opstår et sammenbrud. I denne version er gevinsten sat til fire gange tabet ved at svinge, som vist i figur 16.18 “Kylling”, men du kan ændre spillet og se, hvad der sker.
Figur 16.18 Kylling
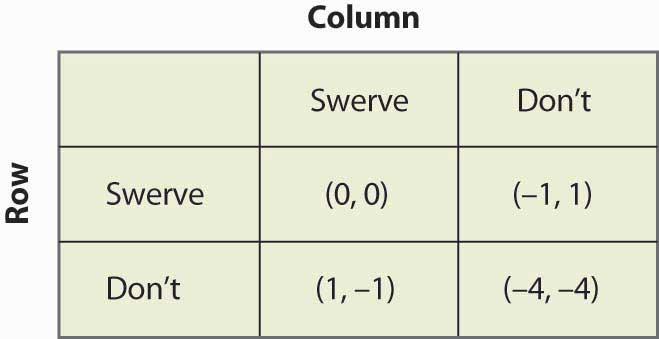
Dette spil har to rene strategiligibrier: (Svinge, ikke) og (ikke, svinge). Desuden har det en blandet strategi. Antag, at Kolonne svinger med sandsynlighed p. Så får Række 0p + -1(1 – p) ved at svinge, 1p + (-4)(1 – p) ved ikke at svinge, og Række vil randomisere, hvis disse er lige store, hvilket kræver p = ¾. Det vil sige, at sandsynligheden for, at kolonnen undviger i en blandet strategi ligevægt er ¾. Du kan verificere, at Row-spilleren har den samme sandsynlighed ved at sætte sandsynligheden for at Row swerves lig med q og beregne Column’s forventede payoffs. Sandsynligheden for en kollision er således 1/16 i den blandede strategi ligevægt.
Den blandede strategi ligevægt er mere sandsynlig, i en vis forstand, i dette spil: Hvis spillerne allerede vidste, hvem der ville give sig, ville de faktisk ikke have behov for at spille spillet. Hele pointen med spillet er at finde ud af, hvem der vil give efter, hvilket betyder, at det ikke er kendt på forhånd. Det betyder, at den blandede strategi ligevægt på en vis måde er den mere fornuftige ligevægt.
Figur 16.19 Sten, papir, saks
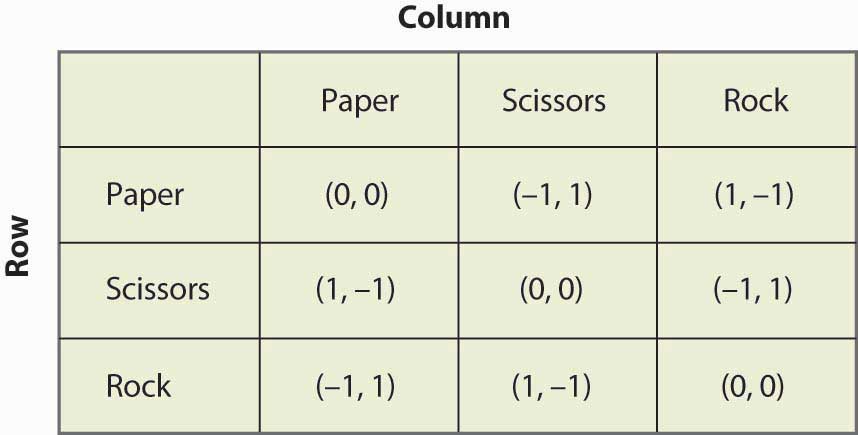
“Sten, papir, saks” er et børnespil, hvor to børn bruger deres hænder til samtidig at vælge papir (hånden holdes flad), saks (hånden med to fingre, der stikker ud, så det ligner en saks) eller sten (hånden holdes i knytnæve). Udbyttet er, at papir slår sten, sten slår saks, og saks slår papir. Dette spil har den struktur, der er illustreret i figur 16.19 “Sten, papir, saks”.
Nøglepunkter
- En Nash-ligevægt med blandet strategi indebærer, at mindst én spiller spiller en randomiseret strategi, og at ingen spiller er i stand til at øge sin forventede gevinst ved at spille en alternativ strategi.
- En Nash-ligevægt uden randomisering kaldes en Nash-ligevægt med ren strategi.
- Hvis en spiller skal randomisere over to strategier, skal begge give den samme forventede gevinst.
- Det matchende penniespil har en blandet strategi og ingen ren strategi.
- Spillet om kønnenes kamp har en blandet strategi og to rene strategier.
- Spillet om kylling ligner kønsstriden og har ligesom den to rene strategier og en blandet strategi.
Opgaver
- Lad q være sandsynligheden for, at Row spiller plat. Vis, at Kolonne er villig til at randomisere, hvis og kun hvis q = ½. (Hint: Beregn først Kolonnens forventede gevinst, når Kolonnen spiller plat, og beregn derefter Kolonnens forventede gevinst, når Kolonnen spiller plat. Disse skal være lige store, for at kolonnen vil randomisere.)
- Vis, at der i sten, papir, saks-spillet ikke findes nogen rene strategilivaler. Vis, at det at spille alle tre handlinger med samme sandsynlighed er en blandet strategi ligevægt.
-
Find alle ligevægte i følgende spil:
Figur 16.20
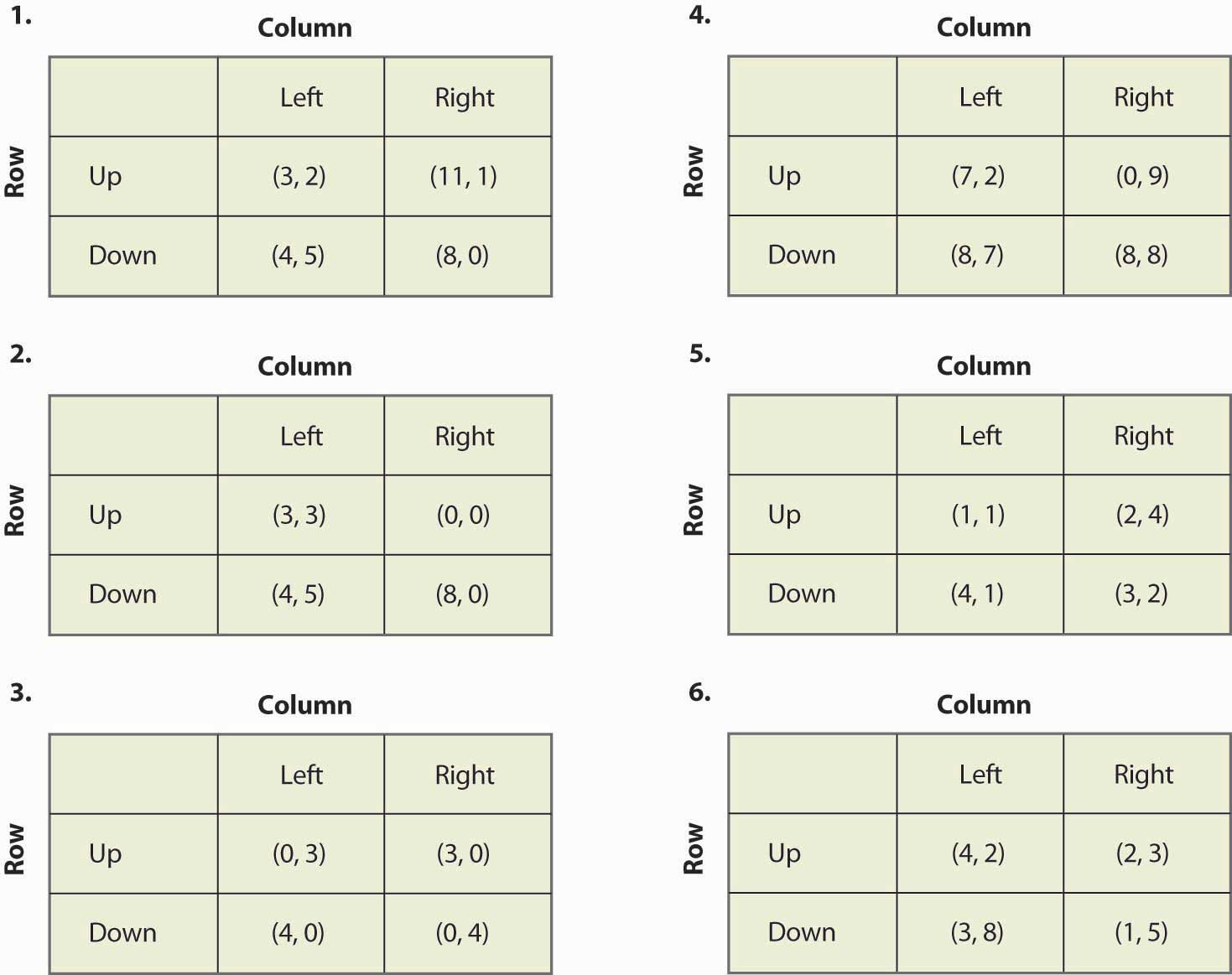
- Hvis man multiplicerer en spillers gevinst med en positiv konstant, ændres spillets ligevægte ikke. Er dette sandt eller falsk, og hvorfor?