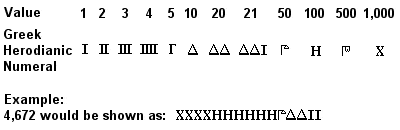
Græske græske herodiske tal
Da det græske imperium begyndte at sprede sin indflydelsessfære til Lilleasien, Mesopotamien og videre ud, var grækerne kloge nok til at overtage og tilpasse nyttige elementer fra de samfund, de erobrede. Dette var lige så sandt for deres matematik som for noget andet, og de overtog elementer af matematik fra både babylonierne og egypterne. Men de begyndte snart at yde vigtige bidrag i deres egen ret, og for første gang kan vi anerkende individuelle bidrag. I den hellenistiske periode havde grækerne stået i spidsen for en af de mest dramatiske og vigtige revolutioner i matematisk tænkning nogensinde.
Attiske eller herodiske tal
Det gamle græske talsystem, kendt som attiske eller herodiske tal, var fuldt udviklet omkring 450 f.v.t. og i regelmæssig brug muligvis allerede i det 7. århundrede f.v.t. Det var et base 10-system, der lignede det tidligere egyptiske system (og endnu mere lignede det senere romerske system), med symboler for 1, 5, 10, 50, 100, 500 og 1.000, der blev gentaget så mange gange som nødvendigt for at repræsentere det ønskede tal. Addition foregik ved at lægge symbolerne (1’er, 10’er, 100’er osv.) i de tal, der skulle lægges sammen, sammen, og multiplikation var en besværlig proces baseret på successive fordoblinger (division var baseret på den omvendte af denne proces).
Thales’ interceptsætning
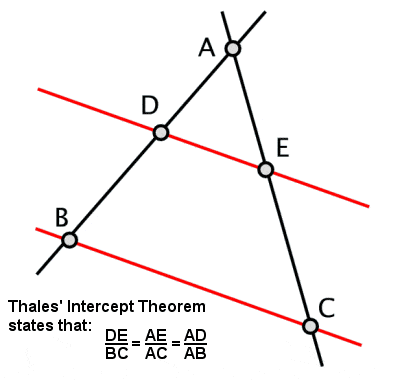
Thales’ interceptsætning
Men det meste af den græske matematik var baseret på geometri. Thales, en af de syv vismænd fra det antikke Grækenland, som levede på den joniske kyst i Lilleasien i første halvdel af det 6. århundrede f.v.t., anses normalt for at have været den første til at fastlægge retningslinjerne for den abstrakte udvikling af geometrien, selv om det, vi kender til hans arbejde (f.eks. om ensartede og retvinklede trekanter), nu synes ret elementært.
Thales opstillede det, der er blevet kendt som Thales’ sætning, hvorefter hvis en trekant tegnes inden for en cirkel med den lange side som en diameter af cirklen, så vil den modsatte vinkel altid være en ret vinkel (samt nogle andre relaterede egenskaber, der er afledt heraf). Han er også krediteret for en anden sætning, også kendt som Thales’ sætning eller Skæringssætningen, om forholdet mellem de linjestykker, der opstår, hvis to skærende linjer skæres af et par paralleller (og i forlængelse heraf forholdet mellem siderne i lignende trekanter).
I et vist omfang er legenden om matematikeren Pythagoras af Samos fra det 6. århundrede f.Kr. imidlertid blevet synonym med den græske matematiks fødsel. Han menes nemlig at have opfundet både ordene “filosofi” (“kærlighed til visdom”) og “matematik” (“det, der er lært”). Pythagoras var måske den første, der indså, at man kunne konstruere et fuldstændigt matematisk system, hvor geometriske elementer svarede til tal. Pythagoras’ sætning (eller den pythagoræiske sætning) er en af de mest kendte af alle matematiske sætninger. Men han er stadig en kontroversiel figur, som vi vil se, og den græske matematik var på ingen måde begrænset til én mand.
Tre geometriske problemer
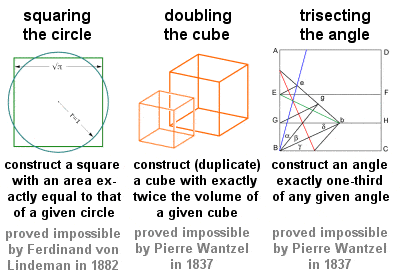
De tre klassiske problemer
Der er især tre geometriske problemer, der ofte omtales som de tre klassiske problemer, og som alle skal løses med rent geometriske midler ved hjælp af kun et lineal og et kompas, og som går tilbage til den græske geometris tidlige dage: “kvadrering (eller kvadratur) af cirklen”, “fordobling (eller fordobling) af terningen” og “tredeling af en vinkel”. Disse uimodståelige problemer fik stor indflydelse på den fremtidige geometri og førte til mange frugtbare opdagelser, selv om deres egentlige løsninger (eller, som det viste sig, beviserne for deres umulighed) måtte vente til det 19. århundrede.
Hippokrates af Chios (ikke at forveksle med den store græske læge Hippokrates af Kos. En detaljeret biografi her.) var en af disse græske matematikere, der beskæftigede sig med disse problemer i det 5. århundrede f.v.t. (hans bidrag til problemet med “kvadrering af cirklen” er kendt som Hippokrates’ Lune). Hans indflydelsesrige bog “The Elements” fra omkring 440 f.Kr. var den første samling af geometriens elementer, og hans arbejde var en vigtig kilde til Euklids senere arbejde.
Zenos paradoks om Achilles og skildpadden
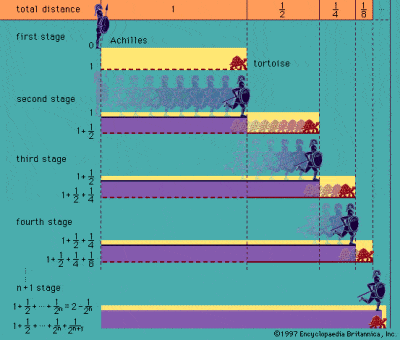
Zenos paradoks om Achilles og skildpadden
Det var grækerne, der først kæmpede med tanken om uendelighed, som beskrevet i de velkendte paradokser, der tilskrives filosoffen Zeno af Elea i det 5. århundrede f.v.t. Det mest berømte af hans paradokser er “Akilles og skildpadden”, som beskriver et teoretisk løb mellem Akilles og en skildpadde. Achilles giver den meget langsommere skildpadde et forspring, men når Achilles når frem til skildpaddens startpunkt, er skildpadden allerede gået foran. Når Achilles når dette punkt, er skildpadden allerede videre igen osv. osv. så den hurtige Achilles kan i princippet aldrig indhente den langsomme skildpadde.
Paradokser som dette og Zenos såkaldte dikotomiparadoks er baseret på rummets og tidens uendelige delelighed og hviler på den tanke, at en halv plus en fjerdedel plus en ottendedel plus en sekstendedel osv. osv. til uendelighed aldrig helt vil blive lig med en helhed. Paradokset stammer imidlertid fra den falske antagelse, at det er umuligt at gennemføre et uendeligt antal diskrete streger på en begrænset tid, selv om det er yderst vanskeligt at bevise denne fejlslutning endeligt. Den græske oldtidsgræker Aristoteles var den første af mange til at forsøge at modbevise paradokset, især fordi han var fast overbevist om, at uendelighed altid kun kunne være potentiel og ikke reel.
Demokrit, der er mest berømt for sine forudseende idéer om, at al materie består af små atomer, var også en pioner inden for matematik og geometri i det 5.-4. århundrede f.v.t., og han udgav værker med titler som “Om tal”, “Om geometri”, “Om tangenter”, “Om kortlægning” og “Om irrationaler”, selv om disse værker ikke er overleveret. Vi ved dog, at han var blandt de første til at konstatere, at en kegle (eller pyramide) har en tredjedel af volumenet af en cylinder (eller prisme) med samme base og højde, og han er måske den første, der seriøst har overvejet opdelingen af objekter i et uendeligt antal tværsnit.
Det er dog helt sikkert rigtigt, at især Pythagoras i høj grad har påvirket dem, der kom efter ham, herunder Platon, der etablerede sit berømte Akademi i Athen i 387 f.Kr. og hans protegé Aristoteles, hvis arbejde om logik blev betragtet som afgørende i over to tusind år. Matematikeren Platon er bedst kendt for sin beskrivelse af de fem platoniske faste legemer, men værdien af hans arbejde som lærer og popularisator af matematikken kan ikke overvurderes.
Platons elev Eudoxus af Cnidus krediteres normalt for den første implementering af “udtømmelsesmetoden” (senere udviklet af Archimedes), en tidlig metode til integration ved successive tilnærmelser, som han brugte til beregning af pyramidens og keglens volumen. Han udviklede også en generel teori om proportioner, som kunne anvendes på inkommensurable (irrationelle) størrelser, der ikke kan udtrykkes som et forhold mellem to hele tal, såvel som på kommensurable (rationelle) størrelser, og som således udvidede Pythagoras’ ufuldstændige ideer.
Men grækernes måske vigtigste enkeltstående bidrag – og Pythagoras, Platon og Aristoteles var alle indflydelsesrige i denne henseende – var ideen om beviser og den deduktive metode, hvor man ved hjælp af logiske trin beviser eller modbeviser teoremer ud fra indledende antagne aksiomer. Ældre kulturer, som f.eks. egypterne og babylonierne, var afhængige af induktiv ræsonnement, dvs. at man brugte gentagne observationer til at opstille tommelfingerregler. Det er dette beviskoncept, der giver matematikken dens styrke og sikrer, at beviste teorier er lige så sande i dag som for to tusind år siden, og som lagde grunden til Euklids og hans efterfølgeres systematiske tilgang til matematikken.
| << Tilbage til egyptisk matematik | Forward to Pythagoras >> |