Chemguide: Support for CIE A level Chemistry
Læringsresultat 11.2(f)
Denne udtalelse handler om fordelingskoefficienter.
Hvor du går videre, bør du finde og læse udtalelsen i dit eksemplar af pensum.
Partition
Hvis man har to umiskelige væsker som f.eks. ether og vand og ryster dem op i en skilletragt, danner de naturligvis to lag. Æteren er mindre tæt end vandet og danner derfor det øverste lag.
Sæt nu, at du ryster en blanding af æter og vand op, som indeholder et stof, der er opløseligt i begge dele. Lad os antage, at stoffet, X, er mere opløseligt i æter end i vand.
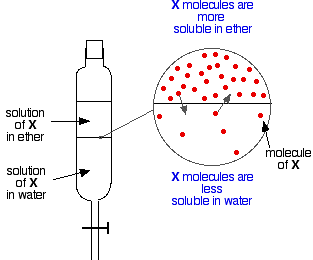
Partikler af X vil krydse grænsen mellem de to væskelag, og du vil snart få en dynamisk ligevægt etableret. For hver partikel, der bevæger sig ind i det øverste lag, vil en partikel bevæge sig tilbage ned i det nederste.
Du kan skrive en ligning for dette:
. . . og som ved enhver anden ligevægt kan man finde en ligevægtskonstant:
Denne ligevægtskonstant kaldes fordelingskoefficienten og får ofte symbolet Kpc.
Som andre ligevægtskonstanter er fordelingskoefficienter konstante ved en konstant temperatur, men de har også nogle andre begrænsninger. De fungerer kun korrekt for ret fortyndede opløsninger, og den opløste stof skal være i samme kemiske form i begge opløsningsmidler. Den må ikke reagere, ionisere eller associeres (f.eks. slutte sig sammen i dimerer).
Beregninger af fordelingskoefficienter
En bemærkning om enheder
Bemærk, at fordelingskoefficienten er et simpelt forhold mellem to koncentrationer. Det er ligegyldigt, hvilke koncentrationsenheder du bruger – så længe du bruger de samme øverst og nederst.
Du kan bruge mol dm-3, men oftest bruger du g cm-3 – gram pr. kubikcentimeter.
Teknisk set kan de firkantede parenteser kun bruges til koncentration i mol dm-3, men i Application Support Booklet og CIE’s karakterskemaer bruges de begge også til andre enheder.
Jeg er ikke indstillet på at gøre det, og jeg skal derfor bruge udtrykket “koncentration af X” i stedet for, hvor ikke-standardiserede koncentrationsenheder anvendes.
Beregning af en fordelingskoefficient
Da en opløsning af 1,00 g X i 100 cm3 vand blev rystet med 10 cm3 ether, blev 0,80 g X overført til etherlaget. Beregn fordelingskoefficienten for X mellem ether og vand.
Hvis du bliver bedt om at beregne en fordelingskoefficient mellem to opløsningsmidler, kommer koncentrationen af det først nævnte opløsningsmiddel oven i Kpc-udtrykket. Så i dette tilfælde:
Du har nok oplysninger til at beregne begge koncentrationer i g cm-3.
Koncentration af X i ether = 0,80/10 g cm-3
Hvis 0,80 g blev overført til ether, er 1,00 – 0,80 g = 0.20 g tilbage i vandet.
koncentration af X i vand = 0,20/100 g cm-3
Så:
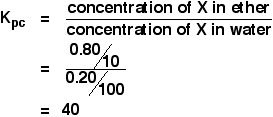
Man kunne naturligvis regne koncentrationerne i ether og i vand ud som faktiske tal, inden man satte dem ind i udtrykket. Gør det på den måde, du føler dig bedst tilpas.
Fordelingskoefficienter som denne har ikke enheder – enhederne ophæver hinanden, fordi de er ens foroven og forneden.
Beregninger med fordelingskoefficienter
I CIE-syllabus står der specifikt, at du skal kunne beregne en fordelingskoefficient (med andre ord, det vi lige har gjort). Der står intet som helst om at bruge dem til at beregne andre ting. Disse ekstra beregninger diskuteres i Application Support Booklet og er blevet spurgt to gange i eksamener frem til juni 2013 (begge gange i 2009).
Kursusbogen indeholder dem ikke (helt korrekt!), fordi pensumplanen ikke nævner dem, og denne bog er blevet godkendt af CIE-eksaminatorer som en “fuldstændig og præcis dækning” af pensumplanen. Betyder det så, at CIE ikke vil stille flere spørgsmål i fremtiden? Regn ikke med det!
Et grundlæggende eksempel
Vi vil bruge den samme sag som tidligere – de samme opløsningsmidler, det samme X og den samme fordelingskoefficient, som vi netop har beregnet.
Denne gang vil vi regne ud, hvor meget der ville være blevet ekstraheret til æterlaget, hvis vi havde omrystet den oprindelige opløsning på 1,00 g X i 100 cm3 vand med blot 5 cm3 æter.
Vi forsøger at regne ud, hvor meget X der er ekstraheret. Lad os kalde det m.
Opnå et udtryk for koncentrationen af opløsningen af X i ether.
koncentration af X i ether = m/5 g cm-3
Hvad med vandet? Der vil være (1,00 – m) g X tilbage i vandet. Så:
koncentration af X i vand = (1,00 – m)/100 g cm-3
Nu kan du sætte alt dette ind i fordelingskoefficientens udtryk. Husk, at vi allerede har beregnet fordelingskoefficienten for X mellem ether og vand til 40.
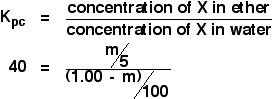
Du står så blot over for en simpel, men lidt kedelig, algebra:
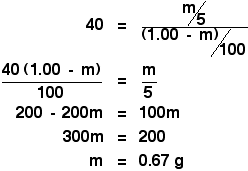
Det er mere kedeligt!
I den oprindelige beregning for at finde fordelingskoefficienten fik du at vide, at hvis du rystede den oprindelige opløsning på 1,00 g X i 100 cm3 vand med 10 cm3 ether, ekstraherede du 0,80 g X.
Rystede du den med 5 cm3 ether, har vi lige regnet ud, at du ville ekstrahere 0,67 g X.
Det ville efterlade 0,33 g X tilbage i de 100 cm3 vand. Lad os antage, at du omhyggeligt havde beholdt denne opløsning og derefter rystet den med endnu en frisk 5 cm3 æter.
Hvor meget X ville du i alt udtrække ved at bruge æteren som to separate partier på 5 cm3 i stedet for de 10 cm3 i én omgang?
Lad os kalde massen af X ekstraheret ved hjælp af det andet parti æter n – så vi ikke bliver forvirrede.
Opnå et udtryk for koncentrationen af opløsningen af X i æter.
koncentration af X i æter = n/5 g cm-3
Hvad med vandet? Der vil være (0,33 – n) g X tilbage i vandet efter den anden ekstraktion. Så:
koncentration af X i vand = (0,33 – n)/100 g cm-3
Nu kan du sætte alt dette ind i fordelingskoefficientudtrykket for X mellem ether og vand som før.
Det betyder, at hvis du kombinerer de to 5 cm3 partier æter, vil du i alt have ekstraheret 0,67 + 0,22 g X. Det er 0.89 g.
Du fik oprindeligt at vide, at hvis du kun havde gjort dette én gang, ved at bruge etteren som et enkelt parti på 10 cm3, ville du kun have ekstraheret 0,80 g.
Du får en mere effektiv ekstraktion ved at opdele dit opløsningsmiddel i mindre mængder som ovenfor.
Denne slags teknik bruger du under fremstillingen af nogle organiske forbindelser. Du ekstraherer det, du forsøger at fremstille, fra en eller anden rodet opløsning i vand, så det ender i et organisk opløsningsmiddel. Derefter fjerner man opløsningsmidlet ved omhyggelig destillation.
CIE stillede et spørgsmål, der ligner dette, i juni 2009 opgave 4 Q8. Du skulle beregne en værdi for fordelingskoefficienten og derefter bruge den i en ekstraktion i to trin præcis som ovenfor. Beregningen var 4 point værd. Dette er måske kedeligt og (bortset fra beregning af fordelingskoefficienten) ikke på pensum, men du har ikke råd til ikke at kunne gøre det.
