Blokdiagrammer består af en enkelt blok eller en kombination af blokke. De bruges til at repræsentere styresystemer i billedform.
Basiselementer i blokdiagram
De grundlæggende elementer i et blokdiagram er en blok, summeringspunktet og afgangspunktet. Lad os betragte blokdiagrammet for et reguleringssystem med lukket kredsløb som vist i følgende figur for at identificere disse elementer.
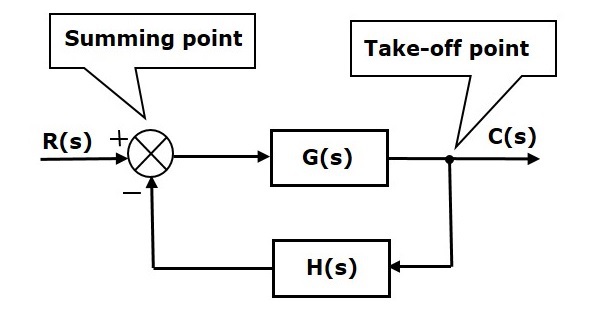
Overstående blokdiagram består af to blokke, der har overførselsfunktionerne G(s) og H(s). Det har også et summeringspunkt og et udtagspunkt. Pilene angiver retningen af signalstrømmene. Lad os nu diskutere disse elementer et for et.
Blok
Overførselsfunktionen for en komponent repræsenteres af en blok. En blok har en enkelt indgang og en enkelt udgang.
Den følgende figur viser en blok med indgang X(s), udgang Y(s) og overførselsfunktionen G(s).

Transferfunktion,$G(s)=\frac{Y(s)}{X(s)}$
$$$\Rightarrow Y(s)=G(s)X(s)$$
Output af blokken fås ved at multiplicere blokens transferfunktion med input.
Summationspunkt
Summationspunktet er repræsenteret med en cirkel med et kryds (X) indeni. Det har to eller flere indgange og en enkelt udgang. Det producerer den algebraiske sum af indgangene. Det udfører også summation eller subtraktion eller en kombination af summation og subtraktion af indgangene baseret på indgangernes polaritet. Lad os se disse tre operationer en for en.
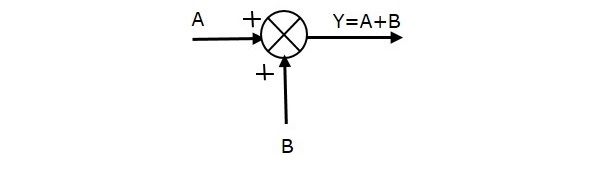
Den følgende figur viser summeringspunktet med to indgange (A, B) og en udgang (Y). Her har indgangene A og B et positivt fortegn. Så summeringspunktet producerer output Y som summen af A og B.
dvs. Y = A + B.
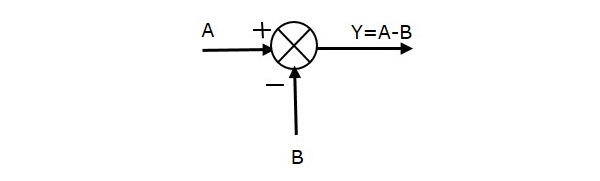
Den følgende figur viser summeringspunktet med to indgange (A, B) og et output (Y). Her har indgangene A og B modsat fortegn, dvs. A har positivt fortegn, og B har negativt fortegn. Så summeringspunktet producerer output Y som forskellen mellem A og B.
Y = A + (-B) = A – B.
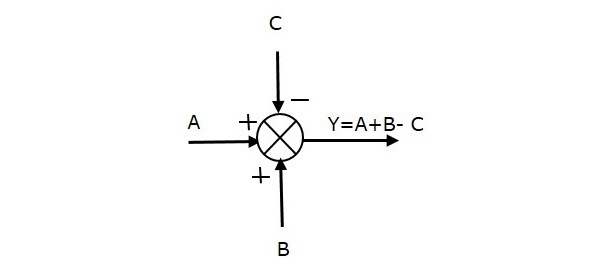
Den følgende figur viser summeringspunktet med tre indgange (A, B, C) og et output (Y). Her har indgangene A og B positive fortegn, og C har et negativt fortegn. Så summeringspunktet producerer output Y som
Y = A + B + (-C) = A + B – C.
Take-off-punkt
Take-off-punktet er et punkt, hvorfra det samme indgangssignal kan ledes gennem mere end én gren. Det betyder, at vi ved hjælp af take-off-punktet kan anvende det samme indgangssignal til en eller flere blokke, summeringspunkter.
I den følgende figur anvendes take-off-punktet til at forbinde det samme indgangssignal, R(s), til yderligere to blokke.
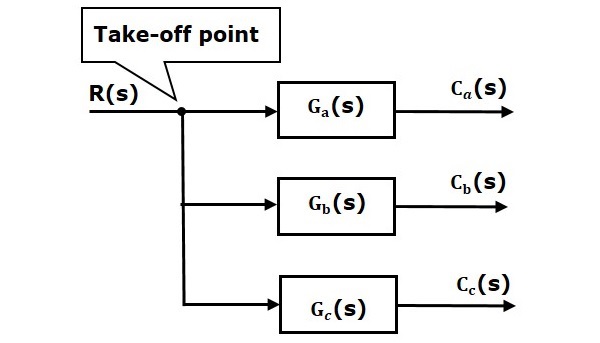
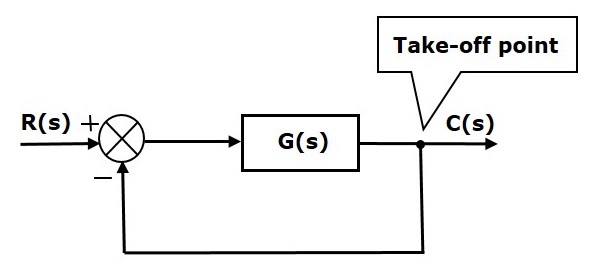
I den følgende figur bruges take-off-punktet til at forbinde udgangen C(s), som en af indgangene til summationspunktet.
Blokdiagramrepræsentation af elektriske systemer
I dette afsnit skal vi repræsentere et elektrisk system med et blokdiagram. Elektriske systemer indeholder hovedsageligt tre grundelementer – modstand, induktor og kondensator.
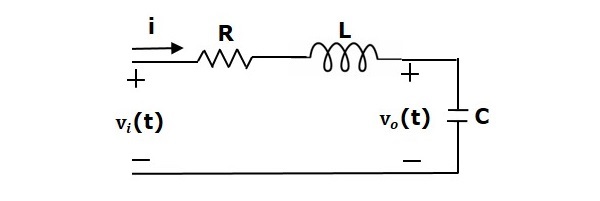
Og tænk på en serie af RLC-kredsløb som vist i følgende figur. Hvor Vi(t) og Vo(t) er indgangs- og udgangsspændingerne. Lad i(t) være den strøm, der passerer gennem kredsløbet. Dette kredsløb er i tidsdomænet.
Ved anvendelse af Laplace-transformationen på dette kredsløb får vi kredsløbet i s-domænet. Kredsløbet er som vist i følgende figur.
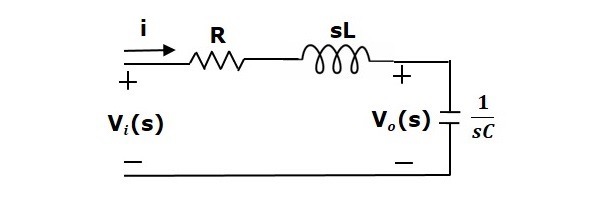
Fra ovenstående kredsløb kan vi skrive
$$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$$
$\Højrefløj I(s)=\venstre \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (Ligning 1)
$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (Ligning 2)
Lad os nu tegne blokdiagrammerne for disse to ligninger hver for sig. Og kombiner derefter disse blokdiagrammer korrekt for at få det samlede blokdiagram for serien af RLC-kredsløb (s-domæne).
Glidning 1 kan implementeres med en blok, der har overførselsfunktionen $\frac{1}{R+sL}$. Indgangen og udgangen af denne blok er $\left \{ V_i(s)-V_o(s) \right \}$ og $I(s)$. Vi har brug for et summeringspunkt for at få $\left \{ V_i(s)-V_o(s) \right \}$. Blokdiagrammet for ligning 1 er vist i følgende figur.
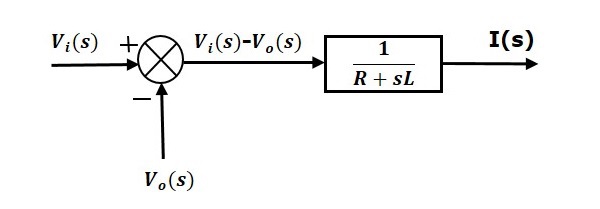
Ligning 2 kan gennemføres med en blok med overførselsfunktion, $\frac{1}{sC}$. Indgangen og udgangen af denne blok er $I(s)$ og $V_o(s)$. Blokdiagrammet for ligning 2 er vist i følgende figur.
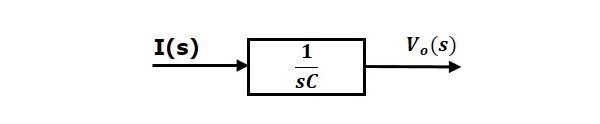
Det overordnede blokdiagram for serien af RLC-kredsløb (s-domæne) er vist i følgende figur.
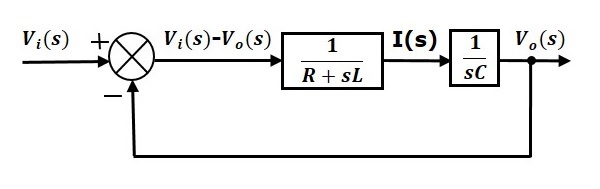
Sådan kan du tegne blokdiagrammet for ethvert elektrisk kredsløb eller system blot ved at følge denne enkle procedure.
-
Konverter det elektriske kredsløb i tidsdomænet til et elektrisk kredsløb i s-domænet ved at anvende Laplace-transformation.
-
Skriv ligningerne ned for den strøm, der passerer gennem alle serieforgreningselementer, og spændingen over alle shuntforgreninger.
-
Tegn blokdiagrammerne for alle ovenstående ligninger enkeltvis.
-
Kombinér alle disse blokdiagrammer korrekt for at få det samlede blokdiagram for det elektriske kredsløb (s-domæne).