Brøker
Brøker kan betragtes som en anden måde at se division på. Hvis du har en hel pizza, og to personer ønsker at dele den ligeligt, vil de dele den i to halvdele:


Korrekte brøker, ukorrekte brøker og blandede tal

Laveste udtryk

Finde den største fælles faktor (GCF)
Den største fælles faktor er den største faktor, der deler to tal. Vi finder den ved at finde ud af, hvilke primtal der er ganget sammen for at danne hvert tal. Et primtal er et tal, der kun kan deles med sig selv eller med et. Eksempler på primtal er 1, 2, 3, 5, 5, 7, 11, 13, 17, 19, 23, 29 osv. Vi ønsker at fokusere på dem, der i de fleste tilfælde er mindre end ti.
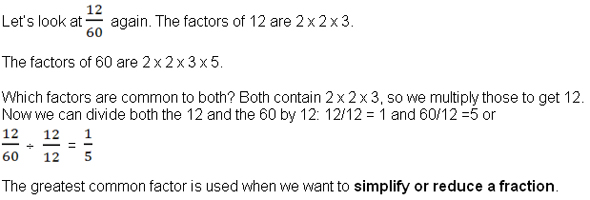
Finde LCD (laveste fællesnævner)

Addere og subtrahere brøker


Multiplikation og division af brøker
Multiplikation af brøker er ret simpelt. Du kan starte med at sætte hver brøk i de laveste termer til at begynde med. Derefter ganges tællerne for at få en tæller og ganges nævnerne for at få en ny nævner. Og reducer eller forenkl brøken for at sætte den i de laveste termer. Hvis du multiplicerer en brøk med et heltal, skal du sætte det hele tal over et for at lave en brøk af det.
Eksempler:
Fem gange 4/5: Sæt fem over et, og multiplicer derefter 5 x 4 for at få 20 og 1 x 5 for at få 5. Tyve kan deles ligeligt med 5 for at få svaret 4.

Gensidighed af brøker
Produktet af et tal og dets gensidighed er lig med 1.

Tegn og brøker
Adderer man to brøker med samme fortegn (enten positive eller negative), får man et svar med samme fortegn. Det kan være nødvendigt at give brøkerne fællesnævner først.

