Talking in Three Dimensions

Se på dette billede af et rektangulært prisme:

Hvor mange hjørner har det? 8

Hvor mange kanter? 12

Hvor mange flader? 6

Nemt, ikke?

Lad os prøve en anden. Tag et kig på dette billede af en kegle:

Hvor mange hjørner har den? Tæller punktet i toppen?

Hvor mange kanter? Hmm, jeg er ikke sikker. Er det ikke meningen, at kanter skal være lige?

Hvor mange flader? Det er nemt! En. Der er en cirkulær flade i bunden. Men det er ikke en polygon, så er det stadig en flade? Åh, og hvad skal jeg kalde den anden flade på keglen? Skal fladerne ikke være flade?

Et almindeligt spørgsmål, som vi får fra lærere i 1., 2. og 3. klasse, drejer sig om, hvordan man beskriver egenskaberne ved visse tredimensionelle faste legemer, især cylindre og kegler. Ifølge TEKS skal eleverne beskrive tredimensionale faste legemer ved hjælp af formelt geometrisk sprog som f.eks. toppunkt, kant og flade. Problemet er, at vi forsøger at bruge et sprog, der fungerer for én klasse af figurer, til at beskrive egenskaberne ved en helt anden klasse.

Tredimensionelle figurer som prismer og pyramider er polyedre. “I geometri er et polyeder simpelthen et tredimensionelt rum, som består af en samling polygoner, der normalt er forbundet ved deres kanter.” (Kilde) Disse faste legemer har “flade polygonale flader, lige kanter og har fælles hjørner eller hjørnepunkter.” (Kilde)

Sfærer, cylindre og kegler er på den anden side ikke polyedre. Som følge heraf kan vi ikke bruge nøjagtigt det samme sprog til at beskrive dem, eller hvis vi bruger det samme sprog, er det med den forståelse, at definitionerne ikke er identiske. Tag f.eks. ordet toppunkt.

På et rektangulært prisme er et toppunkt det skarpe punkt eller hjørne, hvor kanterne mødes. Et rektangulært prisme har 8 hjørner.

Det samme begreb kan imidlertid også bruges til at beskrive punktet i en kegle. Samme udtryk, men ikke samme definition. Som Dr. Math siger,

Den virkelig vanskelige del her er, at “toppunktet” i en kegle ikke har noget med kanter at gøre, så det kræver en helt ny definition; og jeg kan ikke komme i tanke om en rigtig god definition på grundskoleniveau for det, de tydeligvis mener, nemlig simpelthen et “punkt”.”

Når eleverne går videre med mere avanceret matematik, kan de udvikle et mere sofistikeret sprog og mere avancerede definitioner. I mellemtiden, mens de går i folkeskolen, bruger vi i RRISD udtrykket keglens toppunkt til at beskrive denne egenskab ved en kegle.

Hvis vi ønsker, at eleverne skal beskrive og klassificere denne form for tredimensionelt fast stof, så er vi nødt til at give dem et tilgængeligt sprog til det formål.

Hvad med de andre egenskaber ved en kegle? Igen er vores mål at levere et sprog, der er tilgængeligt for elever i grundskolen og beskrivende for disse egenskaber, idet vi erkender, at vores elever vil udvikle mere formelle forståelser senere i deres skolekarriere. For at beskrive en kegle kan vi sige, at den har en cirkulær bund, dvs. den flade overflade, som keglen hviler på. Vi siger også, at den har en buet kant langs bunden og en buet overflade, der strækker sig fra denne kant op til toppunktet.

Hvad med en cylinder? Nu hvor vi har et tilgængeligt sprog til at beskrive egenskaber ved en kegle, kan vi udvide dette sprog til at beskrive egenskaber ved cylindre.

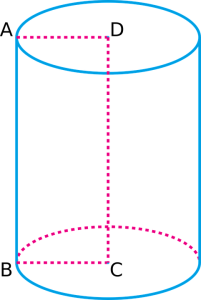
Den ovenstående cylinder består af to cirkulære baser, en på toppen og en på bunden. Den har også to buede kanter, en langs den øverste og en langs den nederste. Endelig har den en buet flade, der strækker sig fra den nederste kant op til den øverste kant.

Jeg bør tilføje, at både den kegle og cylinder, jeg har beskrevet, er en ret cirkelformet kegle og en ret cylinder. Ligesom med polygoner og polyedre findes der mange andre slags eksempler på disse former. For eksempel kan keglen eller cylinderen være skrå, hvilket gør dem skæve.

Det er vigtigt for eleverne at se en række forskellige eksempler på to- og tredimensionelle figurer. Jo flere de møder, jo mere skal de konfronteres med deres definitioner og terminologi, hvilket tjener til at styrke deres forståelse af attributterne, og hvordan de hjælper os med at identificere og klassificere disse figurer.

Så hvordan ser det ud i STAAR?

På den frigivne test fra 2016 stillede STAAR et spørgsmål, der omhandlede netop dette emne og styrkede det ordforråd, vi bruger i RRISD.

Det korrekte svar er F De har ingen hjørner. Hvis du ser på sæt B, vil du bemærke, at det indeholder en kegle, der som vi diskuterede tidligere, har et toppunkt. Hvis Texas Education Agency ikke havde brugt udtrykket keglehjørne, ville vi sandsynligvis have set keglen i sæt A.

Her er en afskedstanke fra Dr. Math:

Hvilken definition du bruger, afhænger af, hvad du vil gøre med den. Hvis du blot beskriver objekter, er min løse definition fin nok. Hvis du skal bevise sætninger, der involverer planer og vinkler, vil du begrænse dig til den polygonale definition, men så vil du ikke stille spørgsmål om kegler. Jeg tror ofte, at folk ikke er klar over, at selv om vi er særlige med hensyn til definitioner i matematik, så varierer disse definitioner fra område til område, da de er tilpasset en bestemt kontekst. Det er det, jeg forsøger at gøre her.