Einführung
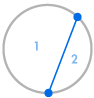
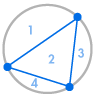
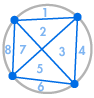
Stellen wir uns vor, wir setzen mehrere Punkte auf den Umfang eines Kreises und verbinden jeden Punkt mit jedem anderen. Dadurch wird der Kreis in viele verschiedene Regionen unterteilt, und wir können die Anzahl der Regionen jeweils zählen. Die folgenden Diagramme zeigen, wie viele Regionen es für verschiedene Anzahlen von Punkten auf dem Kreisumfang gibt. Wir müssen darauf achten, dass sich nur zwei Linien an jedem Schnittpunkt innerhalb des Kreises treffen, nicht drei oder mehr.
 |
 |
 |
 |
 |
| 1 Region | 2 Regionen | 4 Regionen | 8 Regionen | 16 Regionen |
Wir können sofort ein Muster erkennen: Die Anzahl der Regionen ist immer doppelt so groß wie die vorhergehende, so dass wir die Reihenfolge 1, 2, 4, 8, 16, … Das bedeutet, dass es bei 6 Punkten auf dem Umfang 32 Regionen und bei 7 Punkten 64 Regionen geben würde.
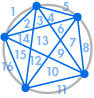
Wir könnten beschließen, dass wir mit diesem Ergebnis zufrieden sind. Die Anzahl der Regionen ist immer doppelt so groß wie die vorherige – schließlich hat das für die ersten fünf Fälle funktioniert. Oder wir beschließen, dass wir sicherheitshalber noch ein paar mehr überprüfen sollten:
 |
 |
| 31 Regionen, nicht 32 | 57 Regionen, nicht 64 |
Dummerweise ist etwas schief gelaufen: 31 mag wie ein Zählfehler aussehen, aber 57 ist viel weniger als 64. Die Folge ist 99, 163, 256, …, ganz anders als bei der Verdopplung der vorherigen Zahl.
Dieses Beispiel zeigt, warum man in der Mathematik nicht einfach sagen kann, dass eine Beobachtung immer wahr ist, nur weil sie in einigen wenigen Fällen, die man getestet hat, funktioniert. Stattdessen muss man sich ein strenges logisches Argument einfallen lassen, das von bereits bekannten Ergebnissen zu etwas Neuem führt, das man als wahr beweisen will. Ein solches Argument nennt man einen Beweis.
Beweise unterscheiden die Mathematik von allen anderen Wissenschaften, denn wenn wir etwas bewiesen haben, sind wir absolut sicher, dass es wahr ist und immer wahr sein wird. Es ist nicht nur eine Theorie, die zu unseren Beobachtungen passt und in der Zukunft durch eine bessere Theorie ersetzt werden kann.
Im obigen Beispiel könnten wir die Anzahl der Schnittpunkte im Inneren des Kreises zählen. Wenn wir sorgfältig über die Beziehung zwischen der Anzahl der Schnittpunkte, der Linien und der Regionen nachdenken, werden wir schließlich zu einer anderen Gleichung für die Anzahl der Regionen führen, wenn es x = V gibt.Axi Punkte auf dem Kreis gibt:
Anzahl der Regionen = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Diese Gleichung funktioniert in allen oben genannten Fällen. Wir könnten nun versuchen, sie für jeden Wert von x zu beweisen, indem wir „Induktion“ verwenden, eine Technik, die weiter unten erklärt wird.
Traditionell wird das Ende eines Beweises mit einem ■ oder □ angezeigt, oder indem man QED oder „quod erat demonstrandum“ schreibt, was lateinisch ist für „was gezeigt werden musste“.
Ein Ergebnis oder eine Beobachtung, von der wir glauben, dass sie wahr ist, wird Hypothese oder Vermutung genannt. Wenn wir sie bewiesen haben, nennen wir sie ein Theorem. Sobald wir ein Theorem bewiesen haben, können wir es verwenden, um andere, kompliziertere Ergebnisse zu beweisen – und so ein wachsendes Netz mathematischer Theoreme aufbauen.
Axiome

Raphaels Schule von Athen: Die antiken griechischen Mathematiker waren die ersten, die sich der Mathematik mit Hilfe eines logischen und axiomatischen Rahmens näherten.
Eine interessante Frage ist, wo man anfangen soll. Wie beweist man das erste Theorem, wenn man noch gar nichts weiß? Leider kann man nicht mit nichts etwas beweisen. Man braucht zumindest ein paar Bausteine, die man Axiome nennt.
Mathematiker nehmen an, dass Axiome wahr sind, ohne sie beweisen zu können. Dies ist jedoch nicht so problematisch, wie es scheinen mag, denn Axiome sind entweder Definitionen oder klar ersichtlich, und es gibt nur sehr wenige Axiome. Ein Axiom könnte zum Beispiel sein, dass a + b = b + a für zwei beliebige Zahlen a und b ist.
Axiome sind wichtig, denn die gesamte Mathematik beruht auf ihnen. Wenn es zu wenige Axiome gibt, kann man nur sehr wenig beweisen und die Mathematik wäre nicht sehr interessant. Wenn es zu viele Axiome gibt, kann man fast alles beweisen, und die Mathematik wäre auch nicht interessant. Man kann auch keine Axiome haben, die sich gegenseitig widersprechen.
In der Mathematik geht es nicht darum, den richtigen Satz von Axiomen zu wählen, sondern darum, aus diesen Ausgangspunkten einen Rahmen zu entwickeln. Wenn man mit anderen Axiomen beginnt, erhält man eine andere Art von Mathematik, aber die logischen Argumente sind dieselben. Jeder Bereich der Mathematik hat seinen eigenen Satz von Grundaxiomen.
Wenn Mathematiker ein Theorem bewiesen haben, veröffentlichen sie es, damit andere Mathematiker es überprüfen können. Manchmal finden sie einen Fehler in der logischen Argumentation, und manchmal wird ein Fehler erst viele Jahre später gefunden. Im Prinzip ist es jedoch immer möglich, einen Beweis in die grundlegenden Axiome zu zerlegen.
Mengentheorie und das Axiom der Wahl

Um Beweise zu formulieren, muss man manchmal auf die Grundlage der Sprache zurückgreifen, in der die Mathematik geschrieben ist: die Mengentheorie.
Eine Menge ist eine Sammlung von Objekten, zum Beispiel Zahlen. Die Elemente einer Menge werden normalerweise in geschweiften Klammern geschrieben. Wir können die Vereinigung zweier Mengen (die Menge der Elemente, die in einer der beiden Mengen enthalten sind) oder die Schnittmenge zweier Mengen (die Menge der Elemente, die in beiden Mengen enthalten sind) finden.
Viele mathematische Probleme können in der Sprache der Mengenlehre formuliert werden, und um sie zu beweisen, brauchen wir Axiome der Mengenlehre. Im Laufe der Zeit haben Mathematiker verschiedene Sammlungen von Axiomen verwendet, wobei die neun Zermelo-Fraenkel (ZF)-Axiome am weitesten verbreitet sind:
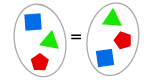
AXIOM DER ERWEITERUNG
Wenn zwei Mengen die gleichen Elemente haben, dann sind sie gleich.
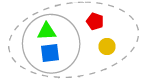
AXIOM DER TRENNUNG
Wir können eine Teilmenge einer Menge bilden, die aus einigen Elementen besteht.

EMPTY SET AXIOM
Es gibt eine Menge ohne Mitglieder, geschrieben als {} oder ∅.
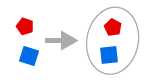
PAIR-SET AXIOM
Gegeben zwei Objekte x und y können wir eine Menge {x, y} bilden.
UNION AXIOM
Wir können die Vereinigung von zwei oder mehr Mengen bilden.
Powerset-Axiom
Von einer beliebigen Menge können wir die Menge aller Teilmengen (das Powerset) bilden.
AXIOM DER UNENDLICHKEIT
Es gibt eine Menge mit unendlich vielen Elementen.

AXIOM DER GRÜNDUNG
Mengen werden aus einfacheren Mengen aufgebaut, d.h. jede (nicht leere) Menge hat ein minimales Mitglied.
AXIOM DER ERSETZUNG
Wenn wir eine Funktion auf jedes Element in einer Menge anwenden, ist die Antwort immer noch eine Menge.
Wenn man über die Mengenlehre nachdenkt, werden die meisten dieser Axiome völlig offensichtlich erscheinen – und das ist es, was Axiome sein sollen. Es gibt jedoch ein zehntes Axiom, das etwas problematischer ist:
AXIOM DER WAHL
Gibt man unendlich viele nicht leere Mengen, so kann man aus jeder dieser Mengen ein Element auswählen.
Auf den ersten Blick sieht das Axiom der Wahl (AC) genauso unschuldig aus wie die anderen oben. Die Verwendung der Unendlichkeit hat jedoch eine Reihe von unerwarteten Konsequenzen. So kann man mit dem AC zum Beispiel beweisen, dass es möglich ist, eine Kugel in fünf Teile zu zerschneiden und sie wieder zusammenzusetzen, um zwei Kugeln zu erhalten, die beide mit der ursprünglichen Kugel identisch sind. Dies ist nur ein theoretisches Konzept – die erforderlichen Schnitte sind fraktal, was bedeutet, dass es sie im wirklichen Leben nicht geben kann, und einige der Teile sind „nicht messbar“, was bedeutet, dass sie kein definiertes Volumen haben. Aber die Tatsache, dass das Axiom der Wahl verwendet werden kann, um diese unmöglichen Schnitte zu konstruieren, ist ziemlich besorgniserregend.
Es gibt eine leidenschaftliche Debatte unter Logikern, ob man das Axiom der Wahl akzeptieren soll oder nicht. Jede Sammlung von Axiomen bildet eine kleine „mathematische Welt“, und verschiedene Theoreme können in verschiedenen Welten wahr sein. Es ist wirklich nur eine Frage, ob man in einer Welt leben möchte, in der man aus einer Kugel zwei Kugeln machen kann…
Beweis durch Induktion
Der Beweis durch Induktion ist eine Technik, mit der man beweisen kann, dass eine bestimmte Aussage für alle natürlichen Zahlen 1, 2, 3, … wahr ist. Die „Aussage“ ist normalerweise eine Gleichung oder Formel, die eine Variable n enthält, die jede natürliche Zahl sein kann. Wir bezeichnen die auf n angewandte Aussage mit S(n). Hier sind die vier Schritte der mathematischen Induktion:
- Zunächst beweisen wir, dass S(1) wahr ist, d.h. dass die Aussage S für 1 wahr ist.
- Nun nehmen wir an, dass S(k) wahr ist, d.h. dass die Aussage S für irgendeine natürliche Zahl k wahr ist.
- Aus dieser Annahme versuchen wir abzuleiten, dass S(k + 1) ebenfalls wahr ist. Wenn also S für eine Zahl wahr ist, ist es auch für die nächste Zahl wahr.
- Da wir wissen, dass S(1) wahr ist, muss auch S(2) wahr sein. Und deshalb muss S(3) wahr sein. Und deshalb muss S(4) wahr sein. Und so weiter: S muss für alle Zahlen wahr sein.

Die Induktion kann mit fallenden Dominosteinen verglichen werden: wenn ein Stein fällt, fällt auch der nächste. Der erste Schritt, der Beweis, dass S(1) wahr ist, setzt die unendliche Kettenreaktion in Gang.
Der erste Schritt wird oft übersehen, weil er so einfach ist. Tatsächlich ist er sehr wichtig und die gesamte Induktionskette hängt von ihm ab – wie einige der folgenden Beispiele zeigen werden…
Das Ziel des Spiels Towers of Hanoi ist es, eine Anzahl von Scheiben von einem Pflock zu einem anderen zu bewegen. Du darfst immer nur eine Scheibe verschieben, und du darfst keine größere Scheibe auf eine kleinere legen. Versuche, den Scheibenturm mit so wenigen Zügen wie möglich vom ersten zum letzten Pflock zu bewegen:
Anzahl der Scheiben: Start Over Moves: 0
Wenn wir die Spielregeln verstanden haben, können wir versuchen, bei einer beliebigen Anzahl von Scheiben die geringste Anzahl von Schritten zu finden. Wenn wir mit dem obigen Spiel spielen, können wir feststellen, dass man bei n Scheiben mindestens 2n – 1 Schritte braucht. Nennen wir diese Aussage S(n).
S(1) ist eindeutig wahr, denn mit nur einer Scheibe braucht man nur einen Zug, und 21 – 1 = 1.
Nehmen wir nun an, dass S(k) wahr ist, d.h. dass man für k Scheiben 2k – 1 Schritte braucht. Wenn wir dann k + 1 Scheiben haben:
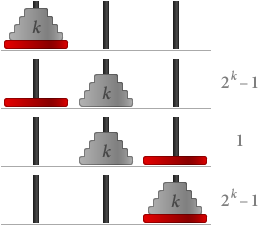
Gesamt benötigen wir (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 Schritte. Das bedeutet, dass S(k + 1) ebenfalls wahr ist.
Durch mathematische Induktion ist S(n) für alle Werte von n wahr, was bedeutet, dass der effizienteste Weg, n = V.Hanoi-Scheiben zu bewegen, 2n – 1 = Math.pow(2,V.Hanoi)-1 Schritte erfordert. ■
Wir wollen durch Induktion beweisen, dass die Summe der ersten n natürlichen Zahlen n (n + 1)2 ist. Wir prüfen die Gleichung zunächst für kleine Werte von n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Nächstens nehmen wir an, dass das Ergebnis für k gilt, d.h. dass 1 + 2 + … + k = k (k + 1)2 ist, wobei k eine Zahl ist, die wir nicht angeben. Nun
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Wir haben soeben bewiesen, dass, wenn die Gleichung für ein bestimmtes k wahr ist, sie auch für k + 1 wahr ist. Durch mathematische Induktion ist die Gleichung für alle Werte von n wahr. ■
Es gibt noch einen anderen cleveren Weg, die obige Gleichung zu beweisen, der keine Induktion verwendet. Angeblich hat Carl Friedrich Gauß (1777 – 1855), einer der größten Mathematiker der Geschichte, diese Methode in der Grundschule entdeckt, als sein Lehrer ihn aufforderte, alle ganzen Zahlen von 1 bis 100 zu addieren.
Wir wollen mit Hilfe der Induktion beweisen, dass alle Menschen die gleiche Haarfarbe haben. S(n) sei die Aussage, dass „jede Gruppe von n Menschen die gleiche Haarfarbe hat“.
Es ist klar, dass S(1) wahr ist: in jeder Gruppe von nur einem Menschen haben alle die gleiche Haarfarbe.
Nehmen wir nun S(k) an, dass in jeder Gruppe von k Menschen alle die gleiche Haarfarbe haben. Wenn wir eine Person in der Gruppe durch eine andere ersetzen, haben sie immer noch insgesamt k und damit die gleiche Haarfarbe. Dies gilt für jede beliebige Ausgangsgruppe, d. h. jede Gruppe von k + 1 hat auch die gleiche Haarfarbe. Daher ist S(k + 1) wahr.
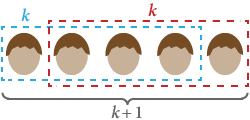
Durch mathematische Induktion haben alle Menschen die gleiche Haarfarbe! ■
Natürlich muss im obigen Beweis etwas falsch gelaufen sein – schließlich haben nicht alle Menschen die gleiche Haarfarbe. Kannst du den Fehler finden?
Einige Theoreme können nicht ganz durch Induktion bewiesen werden – wir müssen eine leicht abgewandelte Version verwenden, die man starke Induktion nennt. Anstatt S(k) anzunehmen, um S(k + 1) zu beweisen, nehmen wir alle von S(1), S(2), … S(k) an, um S(k + 1) zu beweisen. Alles, was mit (schwacher) Induktion bewiesen werden kann, kann offensichtlich auch mit starker Induktion bewiesen werden, aber nicht umgekehrt.
Der Fundamentalsatz der Arithmetik besagt, dass jede ganze Zahl, die größer als 1 ist, entweder eine Primzahl ist, oder dass sie als Produkt von Primzahlen auf eine im Wesentlichen eindeutige Weise geschrieben werden kann.
Wir können Teile davon durch starke Induktion beweisen: S(n) sei die Aussage, dass „die ganze Zahl n eine Primzahl ist oder als Produkt von Primzahlen geschrieben werden kann“. S(1) ist eine Ausnahme, aber S(2) ist eindeutig wahr, weil 2 eine Primzahl ist.
Nun nehmen wir an, dass S(1), S(2), …, S(k) alle wahr sind, für irgendeine ganze Zahl k. Wir wissen, dass k + 1 entweder eine Primzahl ist oder Faktoren kleiner als k + 1 hat. Durch unsere Annahme wissen wir, dass diese Faktoren als das Produkt von Primzahlen geschrieben werden können. Daher kann k + 1, sofern es keine Primzahl ist, auch als Produkt von Primzahlen geschrieben werden. Das bedeutet, dass S(k + 1) wahr ist.
Durch starke Induktion ist S(n) wahr für alle Zahlen n größer als 1. ■
Zu beweisen, dass diese Primfaktorzerlegung eindeutig ist (es sei denn, man zählt verschiedene Reihenfolgen der Faktoren), erfordert mehr Arbeit, ist aber nicht besonders schwer.
Es zeigt sich, dass das Prinzip der schwachen Induktion und das Prinzip der starken Induktion äquivalent sind: jedes impliziert das andere. Sie sind auch beide äquivalent zu einem dritten Satz, dem Wohlordnungsprinzip: Jede (nicht leere) Menge der natürlichen Zahlen hat ein minimales Element, das kleiner ist als alle anderen.
Das Wohlordnungsprinzip ist die definierende Eigenschaft der natürlichen Zahlen. Es ist eines der grundlegenden Axiome, die zur Definition der natürlichen Zahlen ![]() = {1, 2, 3, …} verwendet werden. Diese Axiome werden Peano-Axiome genannt, benannt nach dem italienischen Mathematiker Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …} verwendet werden. Diese Axiome werden Peano-Axiome genannt, benannt nach dem italienischen Mathematiker Guiseppe Peano (1858 – 1932).
Widerspruchsbeweis
Widerspruchsbeweis ist eine weitere wichtige Beweistechnik. Wenn wir eine Aussage S beweisen wollen, nehmen wir an, dass S nicht wahr sei. Mit dieser Annahme versuchen wir, ein falsches Ergebnis abzuleiten, z.B. 0 = 1. Wenn alle unsere Schritte richtig waren und das Ergebnis falsch ist, muss unsere ursprüngliche Annahme falsch gewesen sein. Unsere anfängliche Annahme war, dass S nicht wahr ist, was bedeutet, dass S tatsächlich wahr ist.
Diese Technik kann in vielen verschiedenen Situationen verwendet werden, z. B. um zu beweisen, dass √2 irrational ist, um zu beweisen, dass die reellen Zahlen nicht abzählbar sind, oder um zu beweisen, dass es unendlich viele Primzahlen gibt.
Hier ist ein weiteres lustiges Beispiel:
Wir können den Beweis durch Widerspruch zusammen mit dem Wohlordnungsprinzip verwenden, um zu beweisen, dass alle natürlichen Zahlen „interessant“ sind.
Angenommen, nicht alle natürlichen Zahlen sind interessant, und sei S die Menge der uninteressanten Zahlen. Nach dem Wohlordnungsprinzip hat S ein kleinstes Mitglied x, das die kleinste uninteressante Zahl ist. Diese merkwürdige Eigenschaft macht x eindeutig zu einer besonders interessanten Zahl. Das ist ein Widerspruch, denn wir haben angenommen, dass x uninteressant ist.
Daher sind alle Zahlen interessant. ■
Gödel und die unbeweisbaren Sätze

Kurt Gödel (1906-1978)
Am Anfang des 20. Jahrhunderts begann sich die Mathematik rasant zu entwickeln, und Tausende von Mathematikern arbeiteten in unzähligen neuen Bereichen. David Hilbert (1862 – 1943) stellte ein umfangreiches Programm auf, um die Mathematik zu formalisieren und alle Ungereimtheiten in den Grundlagen der Mathematik zu beseitigen. Dazu gehörte es, alle Theoreme mit Hilfe eines Satzes einfacher und universeller Axiome zu beweisen, zu beweisen, dass dieser Satz von Axiomen konsistent ist, und zu beweisen, dass dieser Satz von Axiomen vollständig ist, d.h. dass jede mathematische Aussage mit Hilfe der Axiome bewiesen oder widerlegt werden kann.
Unglücklicherweise wurden diese Pläne 1931 von Kurt Gödel zerstört. Er bewies, dass man in jedem (hinreichend komplexen) mathematischen System mit einem bestimmten Satz von Axiomen einige Aussagen finden kann, die mit diesen Axiomen weder bewiesen noch widerlegt werden können. Es ist auch nicht möglich zu beweisen, dass ein bestimmter Satz von Axiomen konsistent ist, indem man nichts anderes als die Axiome selbst verwendet.
Gödels Entdeckung basiert auf der Tatsache, dass ein Satz von Axiomen nicht verwendet werden kann, um etwas über sich selbst zu sagen, etwa ob er konsistent ist. Probleme mit der Selbstreferenz finden sich nicht nur in der Mathematik, sondern auch in der Sprache. Hier ist das Lügenparadoxon:
„Dieser Satz ist falsch.“
Der obige Satz versucht, etwas über sich selbst zu sagen. Wenn er wahr ist, dann sagt uns der Satz, dass er falsch ist. Wenn er falsch ist, dann sagt uns der Satz, dass er nicht falsch ist, d.h. dass er wahr ist. In der Tat ist der Satz weder wahr noch falsch.
Als Gödels Theoreme zum ersten Mal veröffentlicht wurden, waren sie für viele Mathematiker sehr beunruhigend. Wenn man sich aufmacht, eine Beobachtung zu beweisen, weiß man nicht, ob es einen Beweis gibt – das Ergebnis könnte wahr, aber unbeweisbar sein. Heute wissen wir, dass die Unvollständigkeit nicht nur in der Logik, sondern auch in der Informatik, die sich auf Maschinen stützt, die logische Operationen ausführen, von grundlegender Bedeutung ist.
Überraschenderweise ist es möglich zu beweisen, dass bestimmte Aussagen unbeweisbar sind. Ein Beispiel ist die Kontinuumshypothese, die sich auf die Größe unendlicher Mengen bezieht.
Gegen Ende seines Lebens entwickelte Kurt Gödel schwere psychische Probleme und starb 1978 an Selbstverhungerung. Seine Einsichten in die Grundlagen der Logik waren die tiefgreifendsten seit der Entwicklung des Beweises durch die alten Griechen.