
Bertrand Russell (1872-1970) und A.N. Whitehead (1861-1947)
Bertrand Russell und Alfred North Whitehead waren britische Mathematiker, Logiker und Philosophen, die an der Spitze der britischen Revolte gegen den kontinentalen Idealismus im frühen 20. Jahrhundert standen und gemeinsam wichtige Beiträge auf dem Gebiet der mathematischen Logik und der Mengenlehre leisteten.
Whitehead war der ältere der beiden und kam aus einer eher rein mathematischen Familie. Er wurde in den 1890er Jahren Russells Tutor am Trinity College in Cambridge und arbeitete dann im ersten Jahrzehnt des 20. Jahrhunderts mit seinem berühmteren ehemaligen Schüler an ihrem monumentalen Werk, den „Principia Mathematica“, zusammen. Nach dem Ersten Weltkrieg, den Russell aufgrund seiner pazifistischen Aktivitäten größtenteils im Gefängnis verbrachte, kam die Zusammenarbeit jedoch zum Erliegen, und Whiteheads akademische Karriere stand fortan im Schatten des schillernden Russell. In den 1920er Jahren emigrierte er in die Vereinigten Staaten und verbrachte dort den Rest seines Lebens.
Russell wurde in eine wohlhabende Familie der britischen Aristokratie hineingeboren, obwohl seine Eltern für die damalige Zeit äußerst liberal und radikal waren. Seine Eltern starben, als Russell noch sehr jung war, und er wurde weitgehend von seiner streng viktorianischen (wenn auch recht fortschrittlichen) Großmutter erzogen. In seiner Jugend war er sehr einsam und litt unter Depressionen, von denen er später behauptete, dass nur seine Liebe zur Mathematik ihn vom Selbstmord abhielt. Er studierte Mathematik und Philosophie an der Universität Cambridge bei G.E. Moore und A.N. Whitehead, wo er sich zu einem innovativen Philosophen, einem produktiven Schriftsteller zu vielen Themen, einem überzeugten Atheisten und einem genialen Mathematiker und Logiker entwickelte. Heute gilt er als einer der Begründer der analytischen Philosophie, aber er schrieb über fast alle wichtigen Bereiche der Philosophie, insbesondere über Metaphysik, Ethik, Erkenntnistheorie, Philosophie der Mathematik und Sprachphilosophie.
Russell war während seines langen Lebens ein engagierter und profilierter politischer Aktivist. Er war ein prominenter Antikriegsaktivist während des Ersten und Zweiten Weltkriegs, setzte sich für Freihandel und Antiimperialismus ein und wurde später zu einem entschiedenen Kämpfer für nukleare Abrüstung und Sozialismus sowie gegen Adolf Hitler, den sowjetischen Totalitarismus und die Beteiligung der USA am Vietnamkrieg.
Russell’s Paradox
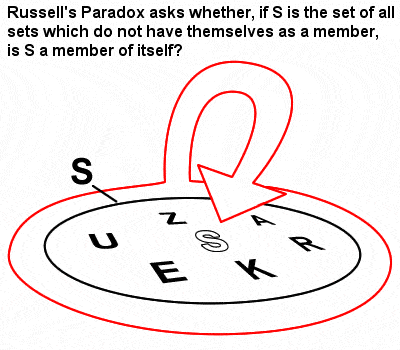
Russell’s Paradox
Russells Mathematik war stark von der Mengenlehre und dem Logizismus Gottlob Freges beeinflusst, die dieser im Gefolge von Cantors bahnbrechenden frühen Arbeiten über Mengen entwickelt hatte. In seinem Werk „The Principles of Mathematics“ aus dem Jahr 1903 entdeckte er jedoch das sogenannte Russell-Paradoxon (eine Menge, die Mengen enthält, die nicht zu sich selbst gehören), das zeigt, dass Freges naive Mengenlehre tatsächlich zu Widersprüchen führen kann.
Das Paradoxon wird manchmal durch dieses einfache Beispiel illustriert: „Wenn ein Barbier alle und nur die Männer im Dorf rasiert, die sich nicht selbst rasieren, rasiert er sich dann selbst?“
Das Paradoxon schien zu implizieren, dass man den Grundlagen der gesamten Mathematik nicht mehr trauen konnte und dass selbst in der Mathematik die Wahrheit niemals absolut bekannt sein konnte (Gödels und Turings spätere Arbeiten würden dies nur noch schlimmer machen). Russells Kritik reichte aus, um Freges Vertrauen in das gesamte Gebäude des Logizismus zu erschüttern, und er war gnädig genug, dies in einem hastig geschriebenen Anhang zu Band II seiner „Grundgesetze der Arithmetik“ offen zuzugeben.
Aber Russells Hauptwerk war die monolithische „Principia Mathematica“, die in drei Bänden in den Jahren 1910, 1912 und 1913 erschien. Der erste Band wurde von Whitehead mitverfasst, die beiden späteren waren jedoch fast ausschließlich Russells Werk. Das Ziel dieses ehrgeizigen Werks war nichts Geringeres als der Versuch, die gesamte Mathematik aus rein logischen Axiomen abzuleiten und dabei die Paradoxien und Widersprüche zu vermeiden, die in Freges früheren Arbeiten zur Mengenlehre zu finden waren. Russell erreichte dies durch die Verwendung einer Theorie oder eines Systems von „Typen“, wobei jede mathematische Einheit einem Typ innerhalb einer Hierarchie von Typen zugeordnet ist, so dass Objekte eines bestimmten Typs ausschließlich aus Objekten vorhergehender Typen, die in der Hierarchie tiefer liegen, gebildet werden, wodurch Schleifen vermieden werden. Jede Menge von Elementen ist also von einem anderen Typ als jedes ihrer Elemente, so dass man nicht von der „Menge aller Mengen“ und ähnlichen Konstruktionen sprechen kann, die zu Paradoxien führen.
Die „Principia“ verlangten jedoch zusätzlich zu den Grundaxiomen der Typentheorie drei weitere Axiome, die als bloße Fragen der Logik nicht wahr zu sein schienen, nämlich das „Unendlichkeitsaxiom“ (das die Existenz mindestens einer unendlichen Menge, nämlich der Menge aller natürlichen Zahlen, garantiert), das „Auswahlaxiom“ (das sicherstellt, dass bei einer beliebigen Sammlung von „Behältern“, die jeweils mindestens ein Objekt enthalten, es möglich ist, genau ein Objekt aus jedem Behälter auszuwählen, selbst wenn es unendlich viele Behälter gibt, und dass es keine „Regel“ dafür gibt, welches Objekt aus jedem Behälter auszuwählen ist) und Russells eigenes „Axiom der Reduzierbarkeit“ (das besagt, dass jede propositionale Wahrheitsfunktion durch eine formal gleichwertige prädikative Wahrheitsfunktion ausgedrückt werden kann).
Während der etwa zehn Jahre, die Russell und Whitehead an den „Principia“ arbeiteten, wurde ein Entwurf nach dem anderen begonnen und wieder verworfen, da Russell seine grundlegenden Prämissen ständig überdachte. Russell und seine Frau Alys zogen sogar bei den Whiteheads ein, um die Arbeit zu beschleunigen, obwohl seine eigene Ehe darunter litt, als Russell sich in Whiteheads junge Frau Evelyn verliebte. Schließlich bestand Whitehead auf der Veröffentlichung des Werkes, auch wenn es nicht vollständig war (und vielleicht nie sein würde), obwohl sie gezwungen waren, es auf eigene Kosten zu veröffentlichen, da kein kommerzieller Verleger es anfassen wollte.
Principia Mathematica

Ein kleiner Teil des langen Beweises, dass 1+1 = 2 in den „Principia Mathematica“
Eine gewisse Vorstellung vom Umfang und der Ausführlichkeit der „Principia“ lässt sich aus der Tatsache ableiten, dass es über 360 Seiten dauert, um endgültig zu beweisen, dass 1 + 1 = 2 ist.
Heute gilt es weithin als eines der wichtigsten und bahnbrechendsten Werke der Logik seit Aristoteles‘ „Organon“. Es schien in seinen ehrgeizigen Zielen bemerkenswert erfolgreich und widerstandsfähig zu sein und verschaffte Russell und Whitehead bald Weltruhm. Erst Gödels Unvollständigkeitssatz von 1931 zeigte schließlich, dass die „Principia“ nicht sowohl konsistent als auch vollständig sein konnten.
Russell wurde 1949 mit dem Verdienstorden und im folgenden Jahr mit dem Nobelpreis für Literatur ausgezeichnet. Sein Ruhm wuchs weiter, auch außerhalb akademischer Kreise, und er wurde in späteren Jahren so etwas wie ein bekannter Name, wenn auch hauptsächlich aufgrund seiner philosophischen Beiträge und seines politischen und sozialen Engagements, das er bis zum Ende seines langen Lebens fortsetzte. Er starb in seinem geliebten Wales im hohen Alter von 97 Jahren an einer Grippe.
| <<Zurück zu Hardy und Ramanujan | Vorwärts zu Hilbert >> |