Chemguide: Support for CIE A level Chemistry
Lernergebnis 11.2(f)
Diese Aussage bezieht sich auf Verteilungskoeffizienten.
Bevor Sie fortfahren, sollten Sie die Aussage in Ihrer Kopie des Lehrplans finden und lesen.
Trennung
Wenn man zwei nicht mischbare Flüssigkeiten wie Äther und Wasser hat und sie in einem Scheidetrichter schüttelt, bilden sie natürlich zwei Schichten. Der Äther hat eine geringere Dichte als das Wasser und bildet daher die oberste Schicht.
Angenommen, man schüttelt eine Mischung aus Äther und Wasser, die einen Stoff enthält, der in beiden löslich ist. Nehmen wir an, dass die Substanz X in Äther besser löslich ist als in Wasser.
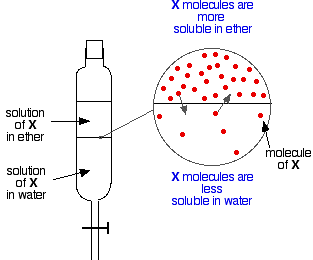
Teilchen von X werden die Grenze zwischen den beiden Flüssigkeitsschichten überschreiten, und bald stellt sich ein dynamisches Gleichgewicht ein. Für jedes Teilchen, das sich in die obere Schicht bewegt, wird eines in die untere zurückwandern.
Dafür könnte man eine Gleichung aufstellen:
. . . und wie bei jedem anderen Gleichgewicht kann man eine Gleichgewichtskonstante finden:
Diese Gleichgewichtskonstante wird Verteilungskoeffizient genannt und wird oft mit dem Symbol Kpc bezeichnet.
Wie andere Gleichgewichtskonstanten sind Verteilungskoeffizienten bei einer konstanten Temperatur konstant, aber sie haben auch einige andere Einschränkungen. Sie funktionieren nur bei ziemlich verdünnten Lösungen richtig, und der gelöste Stoff muss in beiden Lösungsmitteln in derselben chemischen Form vorliegen. Er darf nicht reagieren, ionisieren oder assoziieren (sich z. B. zu Dimeren zusammenschließen).
Berechnungen des Verteilungskoeffizienten
Ein Hinweis zu den Einheiten
Beachten Sie, dass der Verteilungskoeffizient ein einfaches Verhältnis zweier Konzentrationen ist. Es spielt keine Rolle, welche Konzentrationseinheiten du verwendest – solange du oben und unten die gleichen verwendest.
Du könntest mol dm-3 verwenden, aber häufiger verwendet man g cm-3 – Gramm pro Kubikzentimeter.
Technisch gesehen können die eckigen Klammern nur für die Konzentration in mol dm-3 verwendet werden, aber das Application Support Booklet und die CIE-Notenschemata verwenden sie auch für andere Einheiten.
Ich bin nicht bereit, das zu tun, und werde daher den Begriff „Konzentration von X“ verwenden, anstatt nicht standardisierte Konzentrationseinheiten zu verwenden.
Berechnen eines Verteilungskoeffizienten
Wenn eine Lösung von 1,00 g X in 100 cm3 Wasser mit 10 cm3 Ether geschüttelt wurde, wurden 0,80 g X in die Etherschicht überführt. Berechnen Sie den Verteilungskoeffizienten von X zwischen Ether und Wasser.
Wenn Sie aufgefordert werden, einen Verteilungskoeffizienten zwischen zwei Lösungsmitteln zu berechnen, wird die Konzentration des zuerst genannten Lösungsmittels an den Anfang des Kpc-Ausdrucks gestellt. In diesem Fall:
Sie haben also genug Informationen, um beide Konzentrationen in g cm-3 zu berechnen.
Konzentration von X in Ether = 0,80/10 g cm-3
Wenn 0,80 g in den Ether überführt wurden, blieben 1,00 – 0,80 g = 0.20 g blieben im Wasser.
Konzentration von X im Wasser = 0,20/100 g cm-3
So:
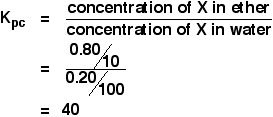
Natürlich könntest du die Konzentrationen im Äther und im Wasser als konkrete Zahlen ausrechnen, bevor du sie in den Ausdruck einsetzt. Mach es so, wie du dich am wohlsten fühlst.
Teilungskoeffizienten wie dieser haben keine Einheiten – die Einheiten heben sich auf, weil sie oben und unten gleich sind.
Berechnungen mit Teilungskoeffizienten
Im CIE-Lehrplan steht ausdrücklich, dass du in der Lage sein sollst, einen Teilungskoeffizienten zu berechnen (mit anderen Worten, das, was wir gerade gemacht haben). Er sagt überhaupt nichts darüber aus, wie man sie zur Berechnung anderer Dinge verwendet. Diese zusätzlichen Berechnungen werden im Application Support Booklet besprochen und wurden bis Juni 2013 zweimal in Prüfungen abgefragt (beide im Jahr 2009).
Das Coursebook enthält sie nicht (ganz richtig!), weil sie im Lehrplan nicht erwähnt werden, und dieses Buch wurde von den CIE-Prüfern als „vollständige und präzise Abdeckung“ des Lehrplans bestätigt. Heißt das also, dass die CIE in Zukunft keine Fragen mehr stellen wird? Verlassen Sie sich nicht darauf!
Ein grundlegendes Beispiel
Wir werden den gleichen Fall wie zuvor verwenden – die gleichen Lösungsmittel, das gleiche X und den gleichen Verteilungskoeffizienten, den wir gerade berechnet haben.
Diesmal werden wir berechnen, wie viel in die Etherschicht extrahiert worden wäre, wenn wir die ursprüngliche Lösung von 1,00 g X in 100 cm3 Wasser mit nur 5 cm3 Ether geschüttelt hätten.
Wir versuchen, die Masse des extrahierten X zu berechnen. Nennen wir sie m.
Bearbeite nun einen Ausdruck für die Konzentration der Lösung von X in Ether.
Konzentration von X in Ether = m/5 g cm-3
Was ist mit dem Wasser? Es verbleiben (1,00 – m) g von X im Wasser. Also:
Konzentration von X in Wasser = (1,00 – m)/100 g cm-3
Nun kannst du all dies in den Ausdruck für den Verteilungskoeffizienten einsetzen. Erinnere dich daran, dass wir bereits den Verteilungskoeffizienten von X zwischen Ether und Wasser als 40 berechnet haben.
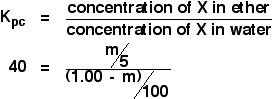
Dann hast du es nur noch mit einem einfachen, aber etwas mühsamen Stück Algebra zu tun:
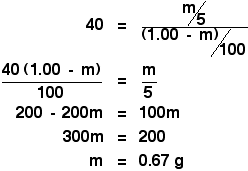
Das macht es noch mühsamer!
In der ursprünglichen Berechnung zur Ermittlung des Verteilungskoeffizienten wurde dir gesagt, dass du, wenn du die ursprüngliche Lösung von 1,00 g X in 100 cm3 Wasser mit 10 cm3 Ether schüttelst, 0,80 g X extrahierst.
Schütteln mit 5 cm3 Ether, wir haben gerade berechnet, dass du 0,67 g X extrahieren würdest.
Damit würden 0,33 g X in den 100 cm3 Wasser zurückbleiben. Angenommen, du hättest diese Lösung sorgfältig aufbewahrt und sie dann mit einem zweiten frischen 5 cm3 Ether geschüttelt.
Wie viel von X würdest du insgesamt extrahieren, wenn du den Ether in zwei getrennten Partien von 5 cm3 statt in einem Durchgang von 10 cm3 verwendest?
Nennen wir die Masse von X, die durch die zweite Menge Äther extrahiert wird, n – damit wir nicht durcheinander kommen.
Bearbeite einen Ausdruck für die Konzentration der Lösung von X in Äther.
Konzentration von X in Äther = n/5 g cm-3
Was ist mit dem Wasser? Nach der zweiten Extraktion verbleiben (0,33 – n) g von X im Wasser. Also:
Konzentration von X im Wasser = (0,33 – n)/100 g cm-3
Nun kann man all dies in den Ausdruck für den Verteilungskoeffizienten von X zwischen Ether und Wasser einsetzen, wie zuvor.
Das bedeutet, dass man, wenn man die beiden 5 cm3 Partien Ether kombiniert, insgesamt 0,67 + 0,22 g X extrahiert hätte. Das sind 0.89 g.
Ursprünglich wurde dir gesagt, dass du nur 0,80 g extrahiert hättest, wenn du dies nur einmal getan hättest, indem du den Ether als eine einzige Charge von 10 cm3 verwendet hättest.
Du erhältst eine effizientere Extraktion, wenn du dein Lösungsmittel in kleinere Volumina aufteilst, wie oben beschrieben.
Diese Art von Technik verwendest du bei der Herstellung einiger organischer Verbindungen. Man extrahiert das, was man herstellen will, aus einer unordentlichen Lösung in Wasser, so dass es in einem organischen Lösungsmittel landet. Das Lösungsmittel wird dann durch vorsichtige Destillation entfernt.
CIE hat im Juni 2009 in Aufgabe 4 Q8 eine ähnliche Frage gestellt. Sie mussten einen Wert für den Verteilungskoeffizienten berechnen und ihn dann in einer zweistufigen Extraktion genau wie oben beschrieben verwenden. Die Berechnung war 4 Punkte wert. Dies mag mühsam sein und steht (abgesehen von der Berechnung des Verteilungskoeffizienten) nicht im Lehrplan, aber Sie können es sich nicht leisten, es nicht zu können.
