Die Delta-Delta-Ct-Methode oder Livak-Methode ist die bevorzugte Methode für die qPCR-Datenanalyse. Sie kann jedoch nur angewandt werden, wenn bestimmte Kriterien erfüllt sind, die im Vorlesungsskript nachgelesen werden können. Falls nicht, ist die Pfaffl-Methode die allgemeinere Methode. Bitte lesen Sie das zusätzliche Lesematerial, um mehr Informationen über diese Methode zu erhalten.
Hier sind die Schritte für die Livak-Methode:
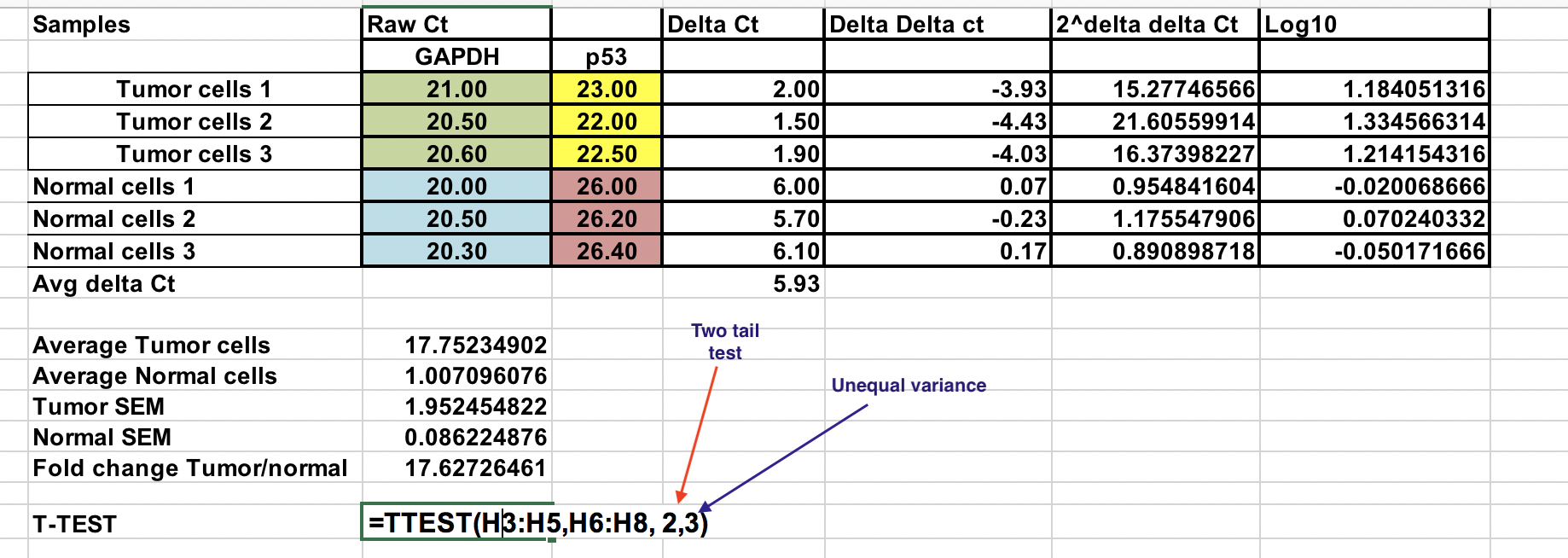
Die Excel-Datei mit allen Berechnungen befinden sich im Ordner qPCR-Analyse auf Blackboard.
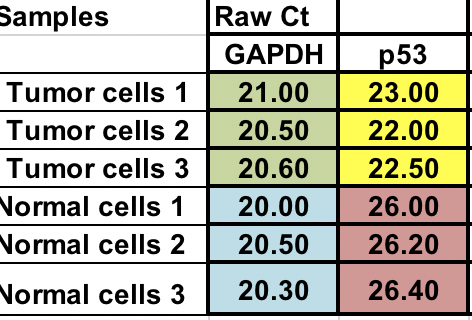
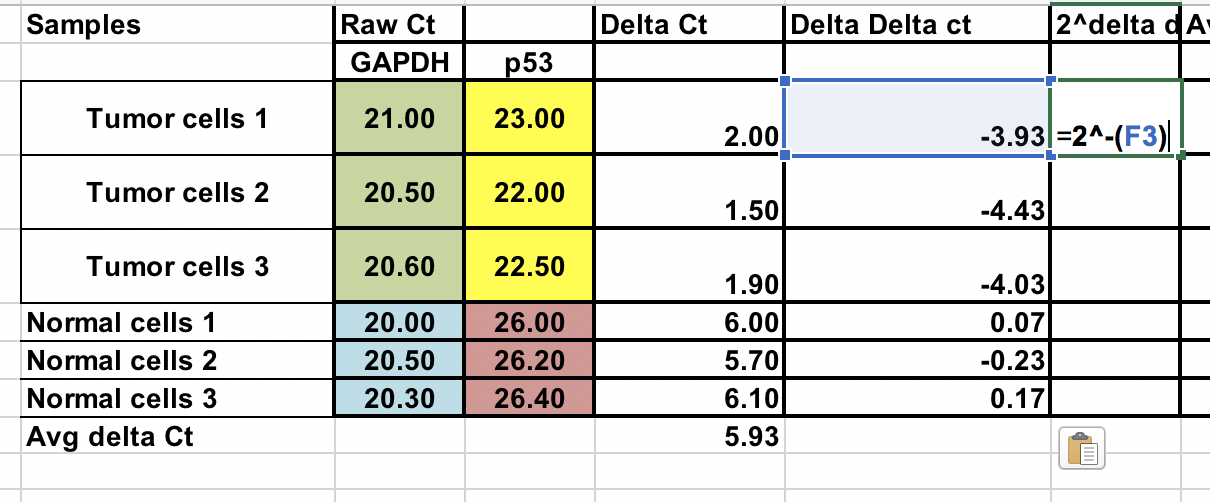
Sie haben rohe Ct-Werte (Anzahl der Zyklen bis zum Erreichen des Schwellenwerts) für normale und Tumorzellen (jeweils 3 Wiederholungen).
Normalisierung¶
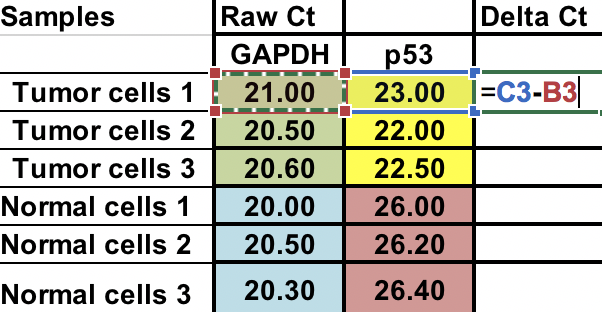
Zunächst müssen Sie die relative Differenz zwischen dem Gen von Interesse (p53) und dem Hausgen (GAPDH) berechnen.
∆Ct = Ct (Gen von Interesse) – Ct (Housekeeping-Gen)
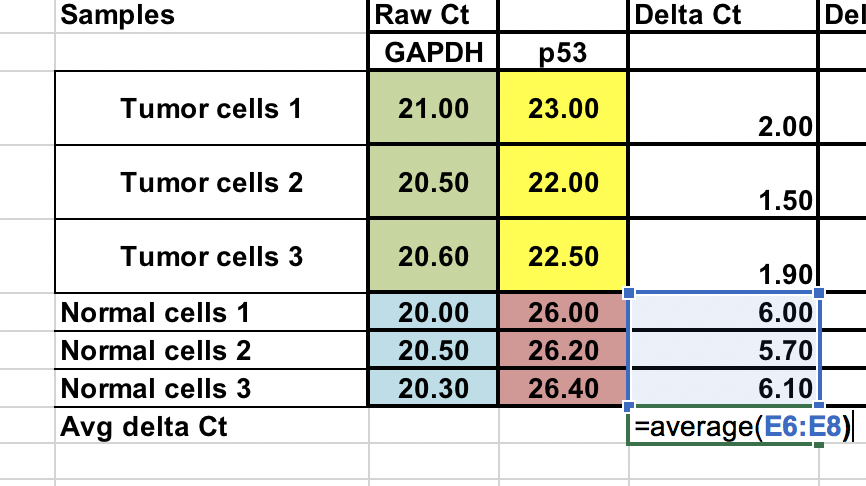
Durchschnitt der Kontrollproben (normale Zellen)¶
Wenn wir unseren Tumor (Behandlung) mit der Kontrolle (normale Zellen) vergleichen, müssen wir zunächst den Durchschnitt der ∆Ct für die 3 Kontrollproben (normale Zellen) bilden.
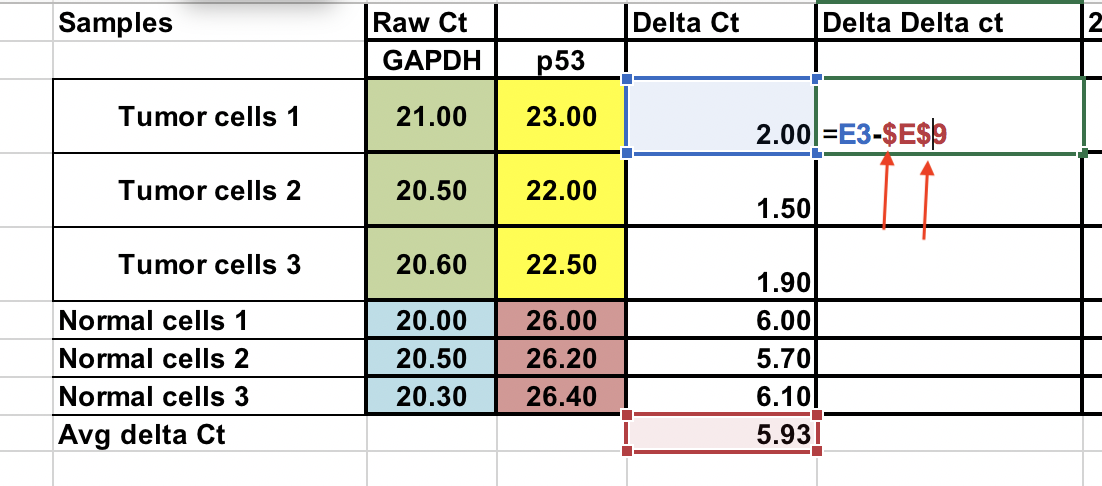
Berechnen Sie die ∆∆Ct relativ zum Durchschnitt der ∆Ct der normalen Zellen¶
∆∆Ct = ∆Ct (Tumorprobe) – ∆Ct (normaler Durchschnitt)
Sie können dies auch mit normalen Proben machen. Verwenden Sie $-Zeichen vor der Spaltennummer und den Rohbuchstaben (Pfeile), um die Zelle zu fixieren.
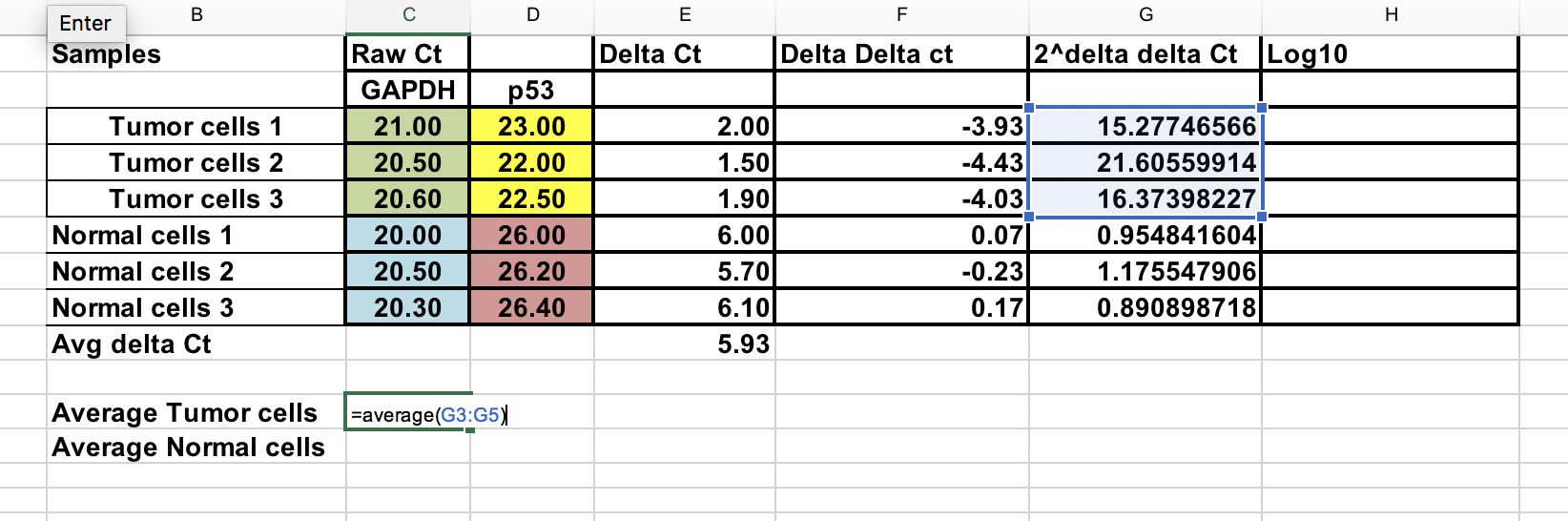
Fache Genexpression für jede Probe¶
Achten Sie darauf, dass Sie das negative ∆∆Ct auf eine Zweierpotenz erhöhen.
Fache Genexpression = 2^-(∆∆Ct)
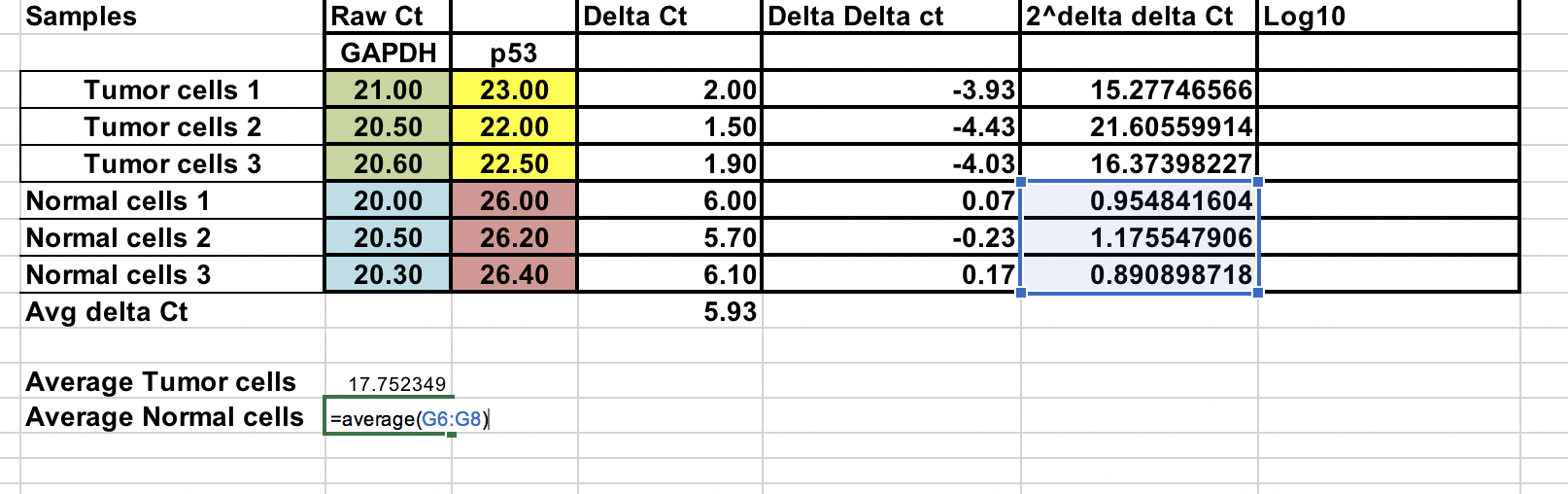
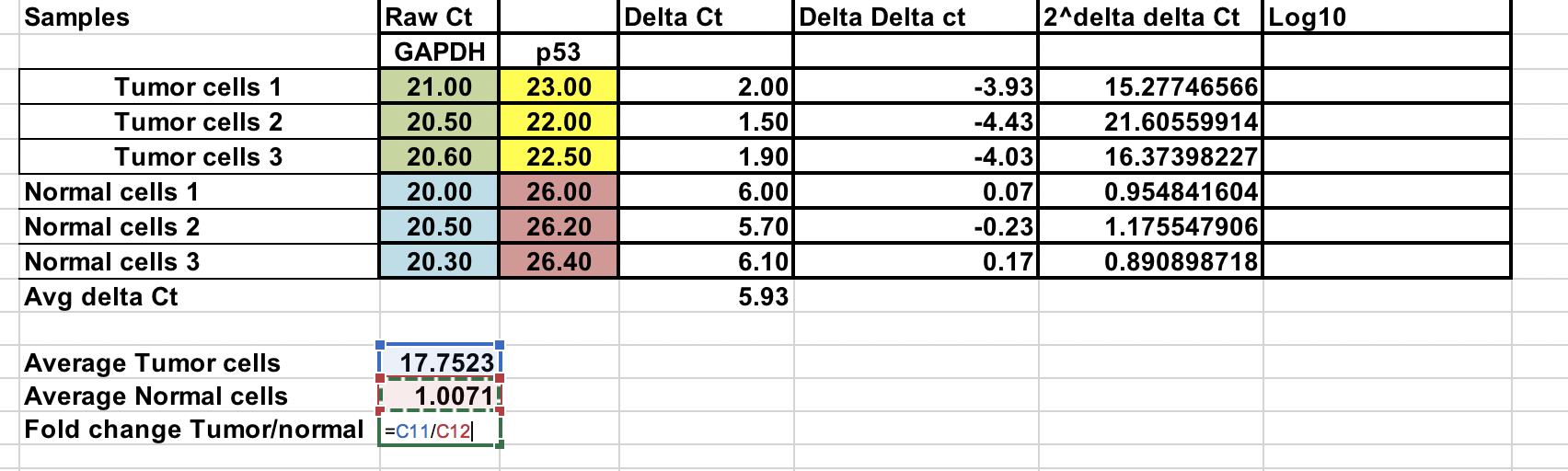
Gesamtfaltenänderung¶
Sie können die durchschnittliche Faltenänderung für Tumor- und Normalproben berechnen. Das Verhältnis zwischen diesen beiden ist die Fold-Change zwischen Tumor- und normalen Proben.
Log-Transformation¶
Um parametrische statistische Tests wie T-Tests durchzuführen, wird empfohlen, die endgültigen Genexpressionsergebnisse in Log-Werte (beliebige Log-Basis) zu transformieren. Dies würde die Datenverteilung symmetrisch machen.
Hier haben wir die 2^-(∆∆Ct) in log 10 geändert.
T-Test¶
Bei der Verwendung parametrischer Tests muss man vorsichtig sein, wenn die Daten nicht normal verteilt sind, da dies zu falschen Schlussfolgerungen führen würde.
Wählen Sie log 10 der 2^-(∆∆Ct)-Werte für normale und Tumorproben wie angegeben. Verwenden Sie den Zwei-Schwanz-Test (Nummer 2) und gehen Sie von ungleicher Varianz (3) aus.
Der resultierende P-Wert ist kleiner als 0,05 und daher lehnen wir die Nullhypothese ab und die beiden Stichprobenmittelwerte sind auf dem 0,05-Niveau signifikant unterschiedlich.