16.3 Gemischte Strategien
Lernziel
- Welche Spiele erfordern oder gestatten die Randomisierung als Teil ihrer Lösung?
Betrachten wir noch einmal das Spiel mit den zusammenpassenden Pfennigen, wie in Abbildung 16 dargestellt.
Abbildung 16.13 „Matching pennies again“
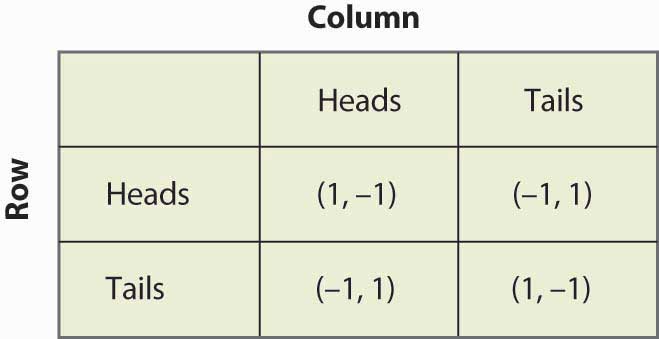
Angenommen, die Reihe glaubt, dass die Spalte mit der Wahrscheinlichkeit p Kopf spielt. Wenn die Reihe Kopf spielt, erhält sie mit der Wahrscheinlichkeit p eine 1 und mit der Wahrscheinlichkeit (1 – p) eine -1, was einem Erwartungswert von 2p – 1 entspricht. In ähnlicher Weise erhält die Reihe, wenn sie auf Zahl spielt, -1 mit der Wahrscheinlichkeit p (wenn die Säule auf Kopf spielt) und 1 mit der Wahrscheinlichkeit (1 – p), was einem Erwartungswert von 1 – 2p entspricht. Dies ist in Abbildung 16.14 „Gemischte Strategie bei passenden Pennys“ zusammengefasst.
Wenn 2p – 1 > 1 – 2p, dann ist Row im Durchschnitt besser dran, wenn sie Kopf als Zahl spielt. Ähnlich verhält es sich, wenn 2p – 1 < 1 – 2p, dann ist die Reihe besser dran, wenn sie Zahl als Kopf spielt. Wenn andererseits 2p – 1 = 1 – 2p ist, dann erhält die Reihe die gleiche Auszahlung, egal was sie tut. In diesem Fall könnte Row Kopf spielen, könnte Zahl spielen oder könnte eine Münze werfen und Row’s Spiel randomisieren.
Ein Nash-Gleichgewicht mit gemischten StrategienEin Nash-Gleichgewicht, bei dem mindestens ein Spieler eine randomisierte Strategie spielt und kein Spieler in der Lage ist, seine erwartete Auszahlung durch das Spielen einer alternativen Strategie zu erhöhen. beinhaltet, dass mindestens ein Spieler eine randomisierte Strategie spielt und kein Spieler in der Lage ist, seine erwartete Auszahlung durch das Spielen einer alternativen Strategie zu erhöhen. Ein Nash-Gleichgewicht, bei dem kein Spieler randomisiert, wird als Nash-Gleichgewicht mit reiner Strategie bezeichnet.
Abbildung 16.14 Gemischte Strategie beim Spiel mit Pennys
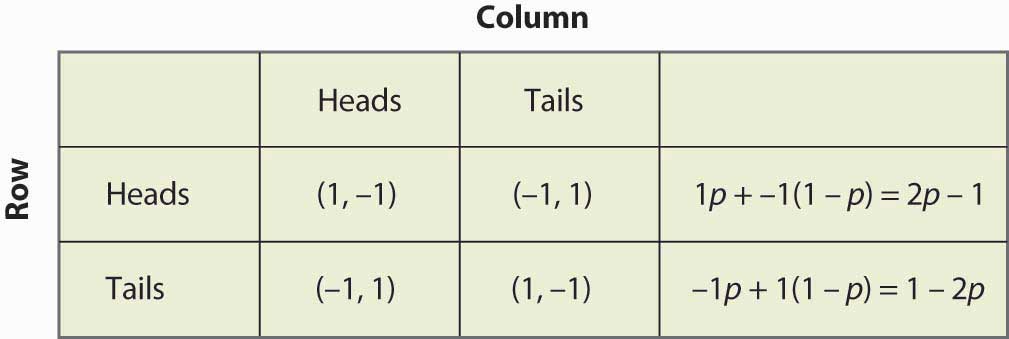
Beachten Sie, dass die Randomisierung Gleichheit der erwarteten Auszahlungen erfordert. Wenn ein Spieler über Strategie A oder Strategie B randomisieren soll, dann müssen beide Strategien die gleiche erwartete Auszahlung bringen. Andernfalls würde der Spieler eine der beiden Strategien vorziehen und die andere nicht spielen.
Die Berechnung einer gemischten Strategie hat ein Element, das oft verwirrend erscheint. Nehmen wir an, dass Row randomisieren wird. Dann müssen die Auszahlungen von Row für alle Strategien, die Row mit positiver Wahrscheinlichkeit spielt, gleich sein. Aber diese Gleichheit in den Auszahlungen der Reihe bestimmt nicht die Wahrscheinlichkeiten, mit denen die Reihe die verschiedenen Reihen spielt. Stattdessen bestimmt diese Gleichheit in den Auszahlungen der Reihe die Wahrscheinlichkeiten, mit denen die Spalte die verschiedenen Spalten spielt. Der Grund dafür ist, dass es die Wahrscheinlichkeiten der Spalten sind, die die erwarteten Auszahlungen für die Reihe bestimmen; wenn die Reihe zufällig spielt, dann müssen die Wahrscheinlichkeiten der Spalten so sein, dass die Reihe bereit ist, zufällig zu spielen.
So haben wir zum Beispiel die Auszahlung für die Reihe berechnet, wenn sie Kopf spielt, was 2p – 1 ist, wobei p die Wahrscheinlichkeit ist, dass die Spalte Kopf spielt. In ähnlicher Weise war die Auszahlung für die Reihe, wenn sie Zahl spielte, 1 – 2p. Die Reihe ist bereit zu randomisieren, wenn diese Werte gleich sind, was p = ½ ergibt.
Nun wollen wir ein etwas schwierigeres Beispiel ausprobieren und den Kampf der Geschlechter wieder aufgreifen. Abbildung 16.15 „Gemischte Strategie im Kampf der Geschlechter“ veranschaulicht die Auszahlungen noch einmal.
Abbildung 16.15 Gemischte Strategie im Kampf der Geschlechter
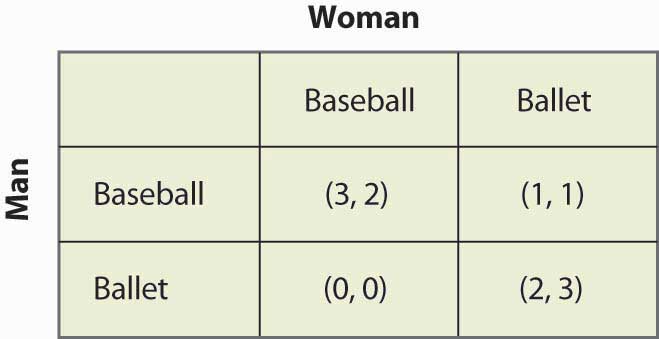
Dieses Spiel hat zwei reine Strategie-Nash-Gleichgewichte: (Baseball, Baseball) und (Ballett, Ballett). Gibt es eine gemischte Strategie? Um eine gemischte Strategie zu berechnen, lassen Sie die Frau mit der Wahrscheinlichkeit p zum Baseball-Spiel gehen und den Mann mit der Wahrscheinlichkeit q zum Baseball-Spiel. Abbildung 16.16 „Vollständige Berechnung der gemischten Strategie“ enthält die Berechnung der Auszahlungen für die gemischte Strategie für jeden Spieler.
Abbildung 16.16 Vollständige Berechnung der gemischten Strategie
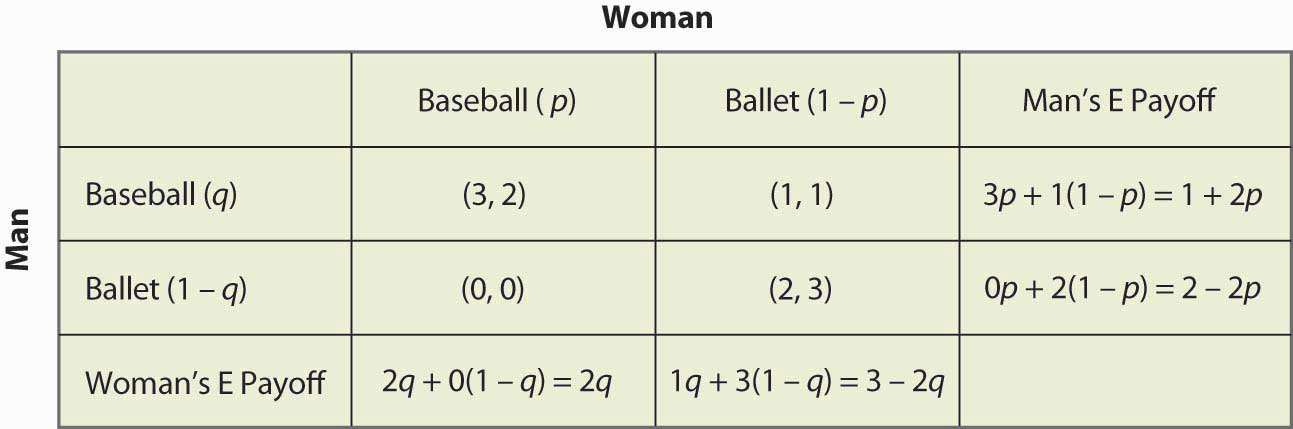
Wenn z.B. der Mann (Reihenspieler) zum Baseballspiel geht, erhält er 3, wenn die Frau zum Baseballspiel geht (Wahrscheinlichkeit p), und ansonsten 1, was einer erwarteten Auszahlung von 3p + 1(1 – p) = 1 + 2p entspricht. Die anderen Berechnungen sind ähnlich, aber Sie sollten auf jeden Fall die Logik durchgehen und jede Berechnung überprüfen.
Eine gemischte Strategie im Spiel „Kampf der Geschlechter“ erfordert, dass beide Parteien randomisieren (da eine reine Strategie einer Partei die Randomisierung der anderen verhindert). Die Gleichgültigkeit des Mannes, ob er zum Baseballspiel oder zum Ballett geht, erfordert 1 + 2p = 2 – 2p, was p = ¼ ergibt. Das bedeutet, dass der Mann bereit ist, nach dem Zufallsprinzip zu entscheiden, welche Veranstaltung er besucht, wenn die Frau in ¾ der Fälle zum Ballett geht, und ansonsten zum Baseballspiel. Damit ist der Mann indifferent zwischen den beiden Veranstaltungen, weil er lieber mit der Frau zusammen ist, aber auch gerne zum Baseballspiel geht. Um den Vorteil, den das Spiel für ihn hat, auszugleichen, muss die Frau öfter ins Ballett gehen.
Damit die Frau randomisieren kann, muss sie die gleichen Auszahlungen erhalten, wenn sie zum Baseballspiel und zum Ballett geht, was 2q = 3 – 2q oder q = ¾ erfordert. Die Wahrscheinlichkeit, dass der Mann zum Baseballspiel geht, beträgt also ¾, und er geht ¼ der Zeit zum Ballett. Dies sind unabhängige Wahrscheinlichkeiten. Um also die Wahrscheinlichkeit zu erhalten, dass beide zum Baseballspiel gehen, multiplizieren wir die Wahrscheinlichkeiten, was 3/16 ergibt. Abbildung 16.17 „Wahrscheinlichkeiten für gemischte Strategien“ füllt die Wahrscheinlichkeiten für alle vier möglichen Ergebnisse aus.
Abbildung 16.17 Wahrscheinlichkeiten für gemischte Strategien
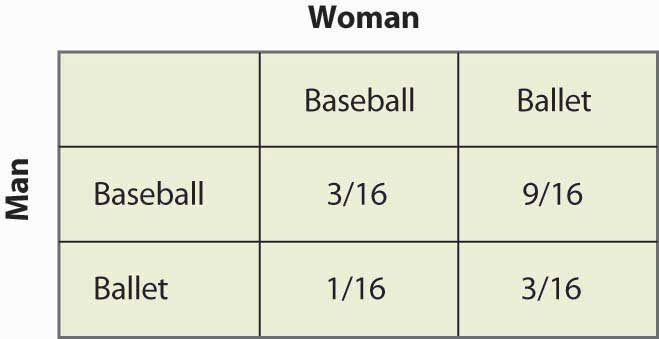
Beachten Sie, dass mehr als die Hälfte der Fälle (Baseball, Ballett) das Ergebnis der gemischten Strategie ist und die beiden Personen nicht zusammen sind. Dieser Mangel an Koordination ist im Allgemeinen ein Merkmal von Gleichgewichten mit gemischter Strategie. Die erwarteten Auszahlungen für beide Spieler lassen sich ebenfalls leicht berechnen. Die Auszahlung des Mannes ist 1 + 2p = 2 – 2p, und da p = ¼ ist, erhält der Mann 1½. Eine ähnliche Berechnung zeigt, dass die Auszahlung der Frau gleich ist. Beide schneiden also schlechter ab, als wenn sie sich auf ihr weniger bevorzugtes Ergebnis einigen. Aber dieses Nash-Gleichgewicht mit gemischter Strategie, so unerwünscht es auch erscheinen mag, ist ein Nash-Gleichgewicht in dem Sinne, dass keine Partei ihre eigene Auszahlung angesichts des Verhaltens der anderen Partei verbessern kann.
Im Kampf der Geschlechter mag das Nash-Gleichgewicht mit gemischter Strategie unwahrscheinlich erscheinen; und wir könnten erwarten, dass das Paar sich effektiver koordiniert. Ein einfaches Telefongespräch sollte die gemischte Strategie eigentlich ausschließen. Betrachten wir also ein anderes Spiel, das mit dem Geschlechterkampf verwandt ist und bei dem ein Scheitern der Koordination sinnvoller ist. Dies ist das Spiel „Huhn“. Bei diesem Spiel fahren zwei Spieler aufeinander zu und versuchen, den anderen zum Ausweichen zu bewegen und schließlich in einen Graben zu fahren. Wenn beide in den Graben ausweichen, gilt das Spiel als unentschieden und beide bekommen null Punkte. Wenn einer ausweicht und der andere nicht, verliert der Fahrer, der ausweicht, und der andere Fahrer gewinnt, und wir geben dem Gewinner einen Punkt.Beachten Sie, dass das Hinzufügen einer Konstante zu den Auszahlungen eines Spielers oder das Multiplizieren der Auszahlungen dieses Spielers mit einer positiven Konstante keinen Einfluss auf die Nash-Gleichgewichte hat – egal ob rein oder gemischt. Daher können wir immer ein Ergebnis für jeden Spieler gleich Null und ein anderes Ergebnis gleich Eins sein lassen. Die einzige verbleibende Frage ist, was passiert, wenn keines der beiden Gleichgewichte aufgeht; in diesem Fall kommt es zu einem Crash. In dieser Version wurde die Auszahlung auf das Vierfache des Verlustes beim Ausweichen festgelegt, wie in Abbildung 16.18 „Huhn“ gezeigt, aber Sie können das Spiel ändern und sehen, was passiert.
Abbildung 16.18 Huhn
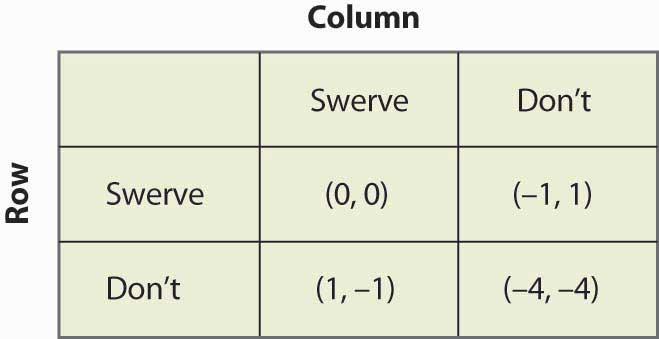
Dieses Spiel hat zwei reine Strategiegleichgewichte: (Ausweichen, nicht ausweichen) und (nicht ausweichen, ausweichen). Darüber hinaus gibt es eine gemischte Strategie. Angenommen, die Kolonne weicht mit der Wahrscheinlichkeit p aus. Dann erhält die Reihe 0p + -1(1 – p), wenn sie ausweicht, 1p + (-4)(1 – p), wenn sie nicht ausweicht, und die Reihe wird zufällig entscheiden, ob diese Werte gleich sind, was p = ¾ erfordert. Das heißt, die Wahrscheinlichkeit, dass die Säule in einem Gleichgewicht mit gemischten Strategien ausweicht, beträgt ¾. Man kann überprüfen, dass der Zeilenspieler die gleiche Wahrscheinlichkeit hat, indem man die Wahrscheinlichkeit, dass die Reihe ausweicht, gleich q setzt und die erwarteten Auszahlungen der Spalte berechnet. Die Wahrscheinlichkeit eines Zusammenstoßes ist also 1/16 im Gleichgewicht der gemischten Strategie.
Das Gleichgewicht der gemischten Strategie ist in gewisser Weise wahrscheinlicher in diesem Spiel: Wenn die Spieler bereits wüssten, wer nachgeben wird, bräuchten sie das Spiel gar nicht zu spielen. Der Sinn des Spiels besteht darin, herauszufinden, wer nachgeben wird, was bedeutet, dass dies nicht im Voraus bekannt ist. Das bedeutet, dass das Gleichgewicht mit gemischten Strategien in gewissem Sinne das vernünftigere Gleichgewicht ist.
Abbildung 16.19 Stein, Papier, Schere
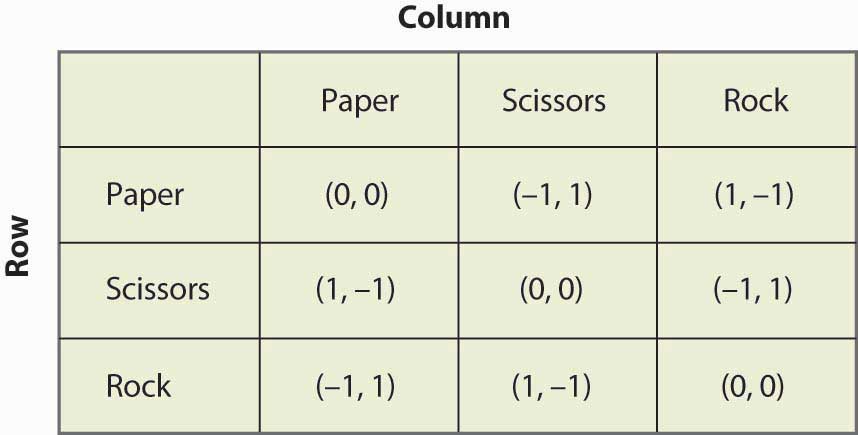
„Stein, Papier, Schere“ ist ein Kinderspiel, bei dem zwei Kinder mit ihren Händen gleichzeitig Papier (flache Hand), Schere (Hand mit zwei abstehenden Fingern, die wie eine Schere aussehen) oder Stein (Hand zur Faust geballt) wählen. Der Gewinn besteht darin, dass Papier gegen Stein, Stein gegen Schere und Schere gegen Papier gewinnt. Dieses Spiel hat die Struktur, die in Abbildung 16.19 „Stein, Papier, Schere“ dargestellt ist.
Key Takeaways
- Ein Nash-Gleichgewicht mit gemischter Strategie beinhaltet, dass mindestens ein Spieler eine randomisierte Strategie spielt und kein Spieler in der Lage ist, seine erwartete Auszahlung durch das Spielen einer alternativen Strategie zu erhöhen.
- Ein Nash-Gleichgewicht ohne Randomisierung wird als Nash-Gleichgewicht mit reiner Strategie bezeichnet.
- Wenn ein Spieler zwischen zwei Strategien randomisieren soll, dann müssen beide die gleiche erwartete Auszahlung erzeugen.
- Das Matching-Pennies-Spiel hat eine gemischte Strategie und keine reine Strategie.
- Das Battle of the Sexes-Spiel hat eine gemischte Strategie und zwei reine Strategien.
- Das Hühnerspiel ähnelt dem Kampf der Geschlechter und hat wie dieses zwei reine Strategien und eine gemischte Strategie.
Übungen
- Lassen Sie q die Wahrscheinlichkeit sein, dass Reihe Kopf spielt. Zeigen Sie, dass Column bereit ist, zu randomisieren, wenn und nur wenn q = ½ ist. (Tipp: Berechnen Sie zuerst die erwartete Auszahlung von Column, wenn Column Kopf spielt, und dann die erwartete Auszahlung von Column, wenn Column Zahl spielt. Diese müssen gleich sein, damit die Säule randomisiert.)
- Zeigen Sie, dass es im Stein-Papier-Schere-Spiel keine reinen Strategiegleichgewichte gibt. Zeigen Sie, dass das Spielen aller drei Aktionen mit gleicher Wahrscheinlichkeit ein Gleichgewicht mit gemischter Strategie ist.
-
Finden Sie alle Gleichgewichte der folgenden Spiele:
Abbildung 16.20
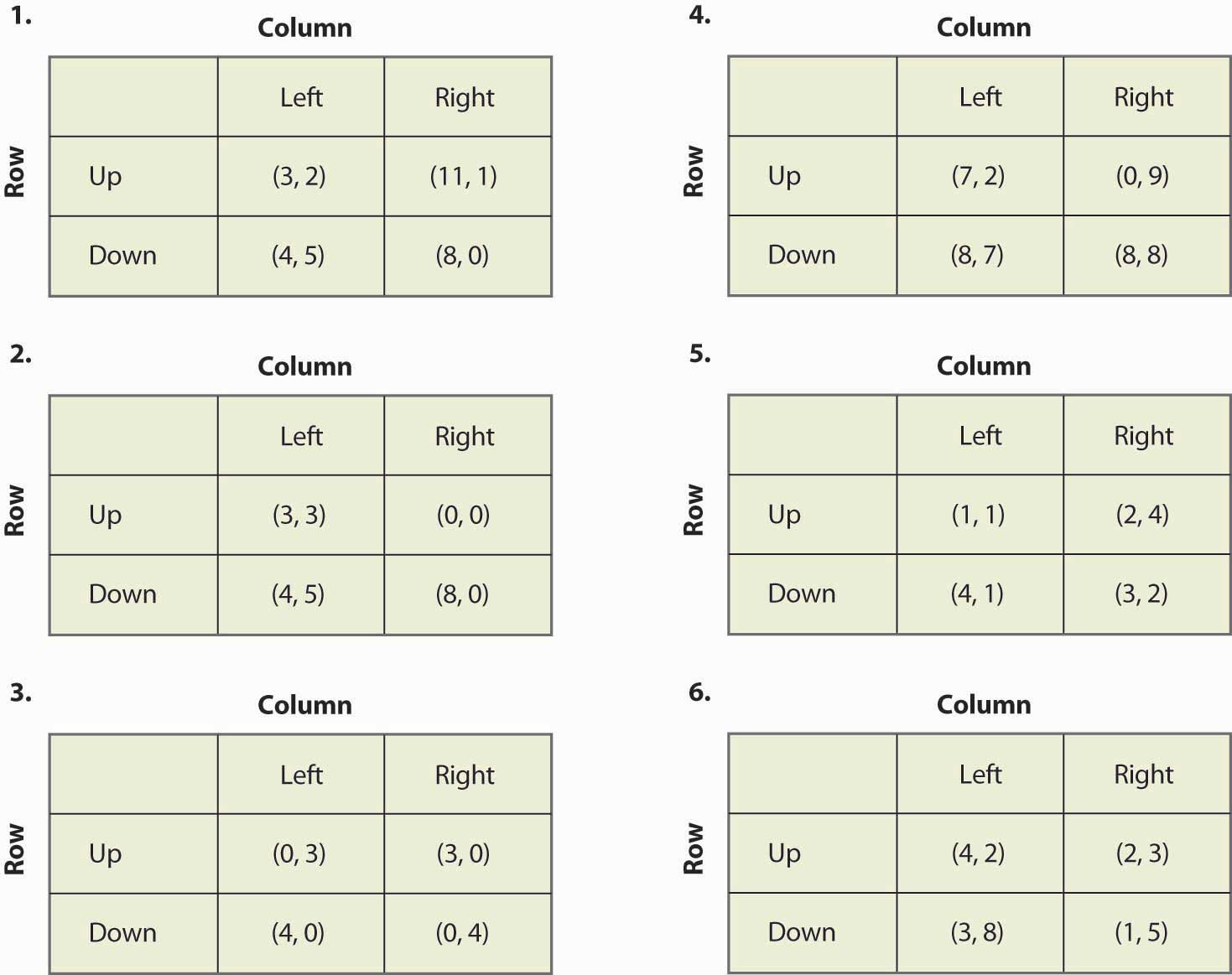
- Wenn man die Auszahlung eines Spielers mit einer positiven Konstante multipliziert, ändern sich die Gleichgewichte des Spiels nicht. Ist dies richtig oder falsch, und warum?