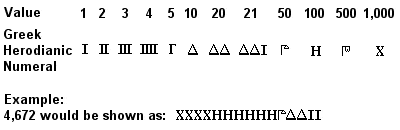
Altgriechische herodianische Ziffern
Als das griechische Reich begann, seinen Einflussbereich nach Kleinasien auszuweiten, Mesopotamien und darüber hinaus auszubreiten, waren die Griechen klug genug, nützliche Elemente aus den eroberten Gesellschaften zu übernehmen und anzupassen. Dies galt auch für ihre Mathematik, und sie übernahmen Elemente der Mathematik sowohl von den Babyloniern als auch von den Ägyptern. Doch schon bald begannen sie, wichtige eigene Beiträge zu leisten, und zum ersten Mal können wir die Beiträge von Einzelpersonen anerkennen. In der hellenistischen Periode leiteten die Griechen eine der dramatischsten und wichtigsten Revolutionen im mathematischen Denken aller Zeiten ein.
Attische oder herodianische Ziffern
Das antike griechische Zahlensystem, das als attische oder herodianische Ziffern bekannt ist, war um 450 v. Chr. voll entwickelt und wurde möglicherweise schon im siebten Jahrhundert v. Chr. regelmäßig verwendet. Es handelte sich um ein System zur Basis 10, das dem früheren ägyptischen (und noch mehr dem späteren römischen) System ähnelte, mit Symbolen für 1, 5, 10, 50, 100, 500 und 1.000, die so oft wiederholt wurden, wie es zur Darstellung der gewünschten Zahl erforderlich war. Die Addition erfolgte durch getrenntes Aufsummieren der Symbole (1er, 10er, 100er usw.) in den zu addierenden Zahlen, und die Multiplikation war ein mühsamer Prozess, der auf aufeinanderfolgenden Verdoppelungen beruhte (die Division basierte auf der Umkehrung dieses Prozesses).
Thales‘ Intercept Theorem
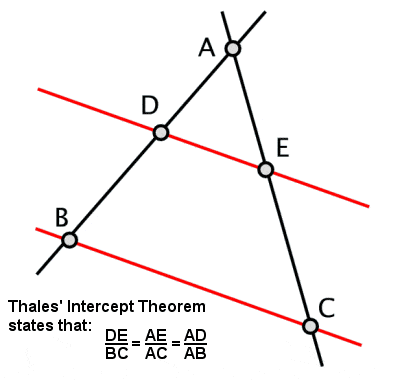
Thales‘ Intercept Theorem
Aber der größte Teil der griechischen Mathematik basierte auf Geometrie. Thales, einer der Sieben Weisen des antiken Griechenlands, der in der ersten Hälfte des 6. Jahrhunderts v. Chr. an der ionischen Küste Kleinasiens lebte, wird gewöhnlich als der erste angesehen, der Richtlinien für die abstrakte Entwicklung der Geometrie festlegte, obwohl das, was wir von seiner Arbeit wissen (z. B. über ähnliche und rechtwinklige Dreiecke), heute recht elementar erscheint.
Thales stellte den so genannten Satz des Thales auf, der besagt, dass, wenn ein Dreieck innerhalb eines Kreises gezeichnet wird und die lange Seite den Durchmesser des Kreises hat, der gegenüberliegende Winkel immer ein rechter Winkel ist (sowie einige andere davon abgeleitete Eigenschaften). Ihm wird auch ein anderes Theorem zugeschrieben, das auch als Thales‘ Theorem oder Abschnittssatz bekannt ist und das sich auf die Verhältnisse der Liniensegmente bezieht, die entstehen, wenn zwei sich schneidende Linien von einem Paar Parallelen abgefangen werden (und damit auch auf die Verhältnisse der Seiten ähnlicher Dreiecke).
Bis zu einem gewissen Grad ist jedoch die Legende des Mathematikers Pythagoras von Samos aus dem 6. Es wird angenommen, dass er sowohl die Worte „Philosophie“ („Liebe zur Weisheit“) als auch „Mathematik“ („das, was man lernt“) geprägt hat. Pythagoras war vielleicht der erste, der erkannte, dass ein vollständiges mathematisches System aufgebaut werden kann, in dem geometrische Elemente mit Zahlen korrespondieren. Der Satz des Pythagoras (oder der Satz des Pythagoras) ist einer der bekanntesten mathematischen Lehrsätze überhaupt. Aber er bleibt eine umstrittene Figur, wie wir sehen werden, und die griechische Mathematik war keineswegs auf einen Mann beschränkt.
Drei geometrische Probleme
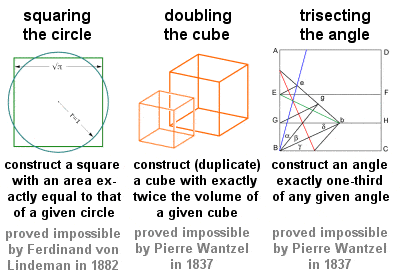
Die drei klassischen Probleme
Besonders drei geometrische Probleme, die oft als die drei klassischen Probleme bezeichnet werden und die alle mit rein geometrischen Mitteln und nur mit Hilfe eines Lineals und eines Zirkels zu lösen sind, gehen auf die frühen Tage der griechischen Geometrie zurück: „die Quadratur des Kreises“, „die Verdoppelung des Würfels“ und „die Dreiteilung eines Winkels“. Diese unnachgiebigen Probleme hatten großen Einfluss auf die künftige Geometrie und führten zu vielen fruchtbaren Entdeckungen, obwohl ihre tatsächlichen Lösungen (oder, wie sich herausstellte, die Beweise für ihre Unmöglichkeit) bis zum 19. Eine ausführliche Biographie finden Sie hier.) war ein solcher griechischer Mathematiker, der sich im 5. Jahrhundert v. Chr. mit diesen Problemen beschäftigte (sein Beitrag zum Problem der „Quadratur des Kreises“ ist als die Lune des Hippokrates bekannt). Sein einflussreiches Buch „Die Elemente“ aus der Zeit um 440 v. Chr. war die erste Zusammenstellung der Elemente der Geometrie, und sein Werk war eine wichtige Quelle für das spätere Werk von Euklid.
Zenos Paradoxon von Achilles und der Schildkröte
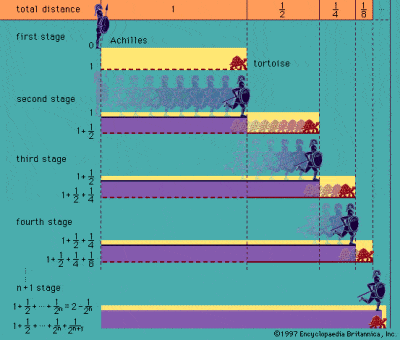
Zenos Paradoxon von Achilles und der Schildkröte
Es waren die Griechen, die sich zum ersten Mal mit der Idee der Unendlichkeit auseinandersetzten, wie sie in den bekannten Paradoxa beschrieben wird, die dem Philosophen Zenon von Elea im 5. Jahrhundert v. Chr. zugeschrieben werden. Das berühmteste seiner Paradoxa ist das von Achilles und der Schildkröte, in dem ein theoretischer Wettlauf zwischen Achilles und einer Schildkröte beschrieben wird. Achilles verschafft der viel langsameren Schildkröte einen Vorsprung, aber wenn Achilles den Ausgangspunkt der Schildkröte erreicht, ist die Schildkröte bereits weitergelaufen. Als Achilles diesen Punkt erreicht, ist die Schildkröte schon wieder weiter usw., so dass der schnelle Achilles die langsame Schildkröte im Prinzip nie einholen kann.
Paradoxien wie dieses und Zenos sogenanntes Dichotomie-Paradoxon beruhen auf der unendlichen Teilbarkeit von Raum und Zeit und auf der Vorstellung, dass eine Hälfte plus ein Viertel plus ein Achtel plus ein Sechzehntel usw. bis zur Unendlichkeit niemals ein Ganzes ergeben kann. Das Paradoxon rührt jedoch von der falschen Annahme her, dass es unmöglich ist, eine unendliche Anzahl diskreter Striche in einer endlichen Zeit zu vollenden, obwohl es äußerst schwierig ist, diesen Trugschluss definitiv zu beweisen. Der antike Grieche Aristoteles war der erste von vielen, der versuchte, die Paradoxa zu widerlegen, zumal er der festen Überzeugung war, dass die Unendlichkeit immer nur potentiell und nicht real sein kann.
Demokrit, der vor allem für seine vorausschauenden Ideen über die Zusammensetzung aller Materie aus winzigen Atomen bekannt ist, war im 5. bis 4. Jahrhundert v. Chr. auch ein Pionier der Mathematik und Geometrie, und er verfasste Werke mit Titeln wie „Über Zahlen“, „Über Geometrie“, „Über Tangenten“, „Über die Abbildung“ und „Über Irrationale“, die allerdings nicht erhalten sind. Wir wissen, dass er zu den ersten gehörte, die feststellten, dass ein Kegel (oder eine Pyramide) ein Drittel des Volumens eines Zylinders (oder Prismas) mit der gleichen Basis und Höhe hat, und er ist vielleicht der erste, der ernsthaft über die Aufteilung von Objekten in eine unendliche Anzahl von Querschnitten nachgedacht hat.
Es ist jedoch sicher richtig, dass insbesondere Pythagoras einen großen Einfluss auf seine Nachfolger hatte, darunter Platon, der 387 v. Chr. seine berühmte Akademie in Athen gründete, und sein Schützling Aristoteles, dessen Werk über die Logik mehr als zweitausend Jahre lang als maßgebend galt. Der Mathematiker Platon ist vor allem für seine Beschreibung der fünf platonischen Körper bekannt, doch kann der Wert seiner Arbeit als Lehrer und Popularisierer der Mathematik gar nicht hoch genug eingeschätzt werden.
Platons Schüler Eudoxus von Cnidus wird gewöhnlich die erste Anwendung der „Methode der Erschöpfung“ zugeschrieben (die später von Archimedes entwickelt wurde), einer frühen Methode der Integration durch sukzessive Annäherung, die er zur Berechnung des Volumens von Pyramide und Kegel verwendete. Er entwickelte auch eine allgemeine Proportionslehre, die sowohl auf inkommensurable (irrationale) Größen, die nicht als Verhältnis zweier ganzer Zahlen ausgedrückt werden können, als auch auf kommensurable (rationale) Größen anwendbar war und damit die unvollständigen Ideen des Pythagoras erweiterte.
Der vielleicht wichtigste Einzelbeitrag der Griechen – und Pythagoras, Platon und Aristoteles waren alle in dieser Hinsicht einflussreich – war die Idee des Beweises und die deduktive Methode, mit der man ausgehend von anfänglich angenommenen Axiomen in logischen Schritten Theoreme beweisen oder widerlegen kann. Ältere Kulturen, wie die Ägypter und die Babylonier, verließen sich auf induktives Denken, d. h. auf wiederholte Beobachtungen, um Faustregeln aufzustellen. Es ist dieses Konzept des Beweises, das der Mathematik ihre Kraft verleiht und sicherstellt, dass bewiesene Theorien heute noch genauso wahr sind wie vor zweitausend Jahren, und das den Grundstein für die systematische Herangehensweise an die Mathematik von Euklid und denen, die nach ihm kamen, legte.
| <<Zurück zur ägyptischen Mathematik | Vorwärts zu Pythagoras >> |