Sprechen in drei Dimensionen

Schauen Sie sich dieses Bild eines rechteckigen Prismas an:

Wie viele Eckpunkte hat es? 8

Wie viele Kanten? 12

Wie viele Flächen? 6

Einfach, nicht wahr?

Lassen Sie uns eine andere versuchen. Schauen wir uns dieses Bild eines Kegels an:

Wie viele Scheitelpunkte hat er? Zählt die Spitze an der Spitze?

Wie viele Kanten? Hmm, ich bin mir nicht sicher. Müssen die Kanten nicht gerade sein?

Wie viele Flächen? Das ist einfach! Eine. Es gibt eine kreisförmige Fläche auf der Unterseite. Aber das ist kein Polygon, also ist es trotzdem eine Fläche? Oh, und wie nenne ich die andere Fläche des Kegels? Müssen Flächen nicht flach sein?

Eine häufige Frage, die wir von Lehrern der Klassen 1, 2 und 3 erhalten, bezieht sich auf die Beschreibung der Eigenschaften bestimmter dreidimensionaler Körper, insbesondere von Zylindern und Kegeln. Gemäß den TEKS sollen die Schüler dreidimensionale Körper mit Hilfe der formalen geometrischen Sprache wie Scheitelpunkt, Kante und Fläche beschreiben. Das Problem ist, dass wir versuchen, eine Sprache zu verwenden, die für eine Klasse von Formen funktioniert, um die Eigenschaften einer völlig anderen Klasse zu beschreiben.

Dreidimensionale Formen wie Prismen und Pyramiden sind Polyeder. „In der Geometrie ist ein Polyeder einfach ein dreidimensionaler Körper, der aus einer Ansammlung von Polygonen besteht, die normalerweise an ihren Kanten verbunden sind.“ (Quelle) Diese Körper haben „flache polygonale Flächen, gerade Kanten und gemeinsame Ecken oder Scheitelpunkte.“ (Quelle)

Kugeln, Zylinder und Kegel sind dagegen keine Polyeder. Folglich können wir nicht genau dieselbe Sprache verwenden, um sie zu beschreiben, oder wenn wir dieselbe Sprache verwenden, dann nur mit dem Verständnis, dass die Definitionen nicht identisch sind. Nehmen wir zum Beispiel das Wort Scheitelpunkt.

Bei einem rechteckigen Prisma ist ein Scheitelpunkt der scharfe Punkt oder die Ecke, an der sich die Kanten treffen. Ein rechteckiges Prisma hat 8 Scheitelpunkte.

Der gleiche Begriff kann aber auch für die Spitze eines Kegels verwendet werden. Gleicher Begriff, aber nicht die gleiche Definition. Wie Dr. Math sagt,

Das wirklich Knifflige daran ist, dass der „Scheitelpunkt“ eines Kegels nichts mit Kanten zu tun hat, so dass eine ganz neue Definition erforderlich ist; und mir fällt keine wirklich gute Definition auf Grundschulniveau für das ein, was sie offensichtlich meinen, nämlich einfach einen „Punkt“.“

Wenn die Schüler fortgeschrittenere Mathematik betreiben, können sie eine anspruchsvollere Sprache und Definitionen entwickeln. In der Zwischenzeit, solange sie in der Grundschule sind, verwenden wir in RRISD den Begriff Scheitelpunkt eines Kegels, um dieses Attribut eines Kegels zu beschreiben.

Wenn wir wollen, dass die Schüler diese Art von dreidimensionalem Körper beschreiben und klassifizieren, dann müssen wir eine zugängliche Sprache für diesen Zweck bereitstellen.

Was ist mit den anderen Attributen eines Kegels? Auch hier ist es unser Ziel, eine Sprache zu verwenden, die für Grundschüler zugänglich ist und diese Eigenschaften beschreibt, wobei wir uns bewusst sind, dass unsere Schüler später in ihrer Schullaufbahn ein formaleres Verständnis entwickeln werden. Um einen Kegel zu beschreiben, würden wir sagen, dass er eine kreisförmige Basis hat, also die flache Oberfläche, auf der der Kegel ruht. Wir sagen auch, dass er eine gekrümmte Kante entlang der Basis und eine gekrümmte Fläche hat, die sich von dieser Kante bis zum Scheitelpunkt erstreckt.

Was ist mit einem Zylinder? Da wir nun eine zugängliche Sprache haben, um die Eigenschaften eines Kegels zu beschreiben, können wir diese Sprache erweitern, um die Eigenschaften von Zylindern zu beschreiben.

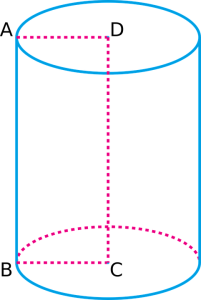
Der obige Zylinder besteht aus zwei kreisförmigen Basen, einer oben und einer unten. Außerdem hat er zwei gekrümmte Kanten, eine oben und eine unten. Schließlich hat er eine gekrümmte Oberfläche, die sich von der unteren Kante bis zur oberen Kante erstreckt.

Ich sollte hinzufügen, dass sowohl der Kegel als auch der Zylinder, die ich beschrieben habe, ein rechter Kreiskegel und ein rechter Zylinder sind. Wie bei Polygonen und Polyedern gibt es viele andere Arten von Beispielen für diese Formen. Der Kegel oder der Zylinder können zum Beispiel schräg sein, so dass sie schief sind.

Es ist wichtig, dass die Schüler eine Vielzahl von Beispielen für zwei- und dreidimensionale Figuren sehen. Je mehr sie sehen, desto mehr müssen sie sich mit den Definitionen und der Terminologie auseinandersetzen, was ihr Verständnis der Attribute und der Art und Weise, wie sie uns helfen, diese Figuren zu identifizieren und zu klassifizieren, stärkt.

Wie sieht das nun bei STAAR aus?

Im 2016 veröffentlichten Test stellte STAAR eine Frage, die genau dieses Thema ansprach und das Vokabular, das wir in RRISD verwenden, verstärkte.

Die richtige Antwort ist F Sie haben keine Scheitelpunkte. Wenn du dir die Menge B ansiehst, wirst du feststellen, dass sie einen Kegel enthält, der, wie wir bereits besprochen haben, einen Scheitelpunkt hat. Wenn die texanische Bildungsbehörde nicht den Begriff Scheitelpunkt eines Kegels verwendet hätte, dann wäre der Kegel wahrscheinlich in Menge A enthalten.

Hier ein abschließender Gedanke von Dr. Math:

Welche Definition man verwendet, hängt davon ab, was man damit machen will. Wenn du nur Objekte beschreibst, ist meine lockere Definition in Ordnung. Wenn Sie Theoreme mit Ebenen und Winkeln beweisen wollen, sollten Sie sich auf die polygonale Definition beschränken, aber dann werden Sie keine Fragen über Kegel stellen. Ich denke, dass die Leute oft nicht erkennen, dass, obwohl wir in der Mathematik bestimmte Definitionen verwenden, diese Definitionen von Bereich zu Bereich variieren, da sie an einen bestimmten Kontext angepasst sind. Genau das versuche ich hier zu tun.