Blockdiagramme bestehen aus einem einzelnen Block oder einer Kombination von Blöcken. Sie werden zur bildlichen Darstellung von Steuerungssystemen verwendet.
Grundelemente des Blockdiagramms
Die Grundelemente eines Blockdiagramms sind ein Block, der Summationspunkt und der Abgriffspunkt. Betrachten wir das Blockdiagramm eines geschlossenen Regelkreises, wie es in der folgenden Abbildung dargestellt ist, um diese Elemente zu identifizieren.
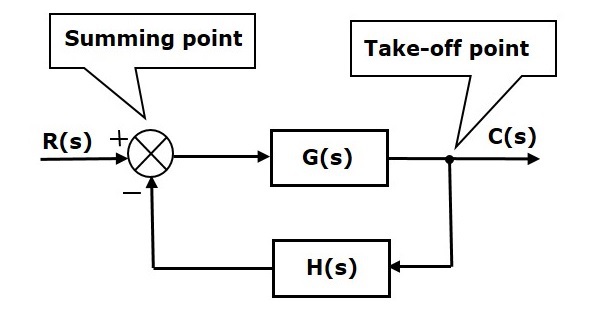
Das obige Blockdiagramm besteht aus zwei Blöcken mit den Übertragungsfunktionen G(s) und H(s). Außerdem gibt es einen Summationspunkt und einen Abzugspunkt. Die Pfeile zeigen die Richtung des Signalflusses an. Lassen Sie uns nun diese Elemente einzeln besprechen.
Block
Die Übertragungsfunktion einer Komponente wird durch einen Block dargestellt. Ein Block hat einen einzigen Eingang und einen einzigen Ausgang.
Die folgende Abbildung zeigt einen Block mit Eingang X(s), Ausgang Y(s) und der Übertragungsfunktion G(s).

Übertragungsfunktion,$G(s)=\frac{Y(s)}{X(s)}$
$$\Rechtspfeil Y(s)=G(s)X(s)$$
Den Ausgang des Blocks erhält man durch Multiplikation der Übertragungsfunktion des Blocks mit dem Eingang.
Summenpunkt
Der Summenpunkt wird durch einen Kreis mit einem Kreuz (X) darin dargestellt. Er hat zwei oder mehr Eingänge und einen einzigen Ausgang. Er erzeugt die algebraische Summe der Eingänge. Er führt auch die Summierung oder Subtraktion oder eine Kombination aus Summierung und Subtraktion der Eingänge durch, je nach Polarität der Eingänge. Sehen wir uns diese drei Operationen nacheinander an.
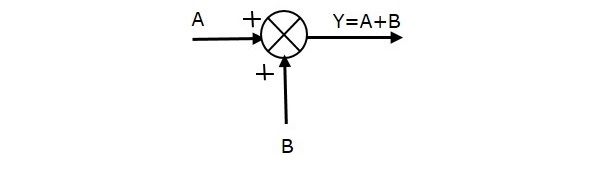
Die folgende Abbildung zeigt den Summierpunkt mit zwei Eingängen (A, B) und einem Ausgang (Y). Hier haben die Eingänge A und B ein positives Vorzeichen. Der Summierpunkt erzeugt also den Ausgang Y als Summe von A und B.
d.h.,Y = A + B.
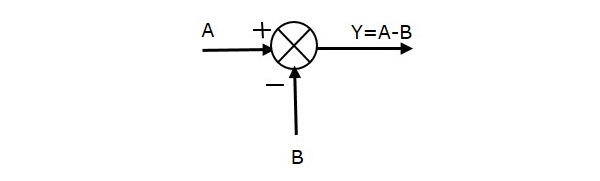
Die folgende Abbildung zeigt den Summierpunkt mit zwei Eingängen (A, B) und einem Ausgang (Y). Hier haben die Eingänge A und B entgegengesetzte Vorzeichen, d.h. A hat ein positives Vorzeichen und B ein negatives Vorzeichen. Der Summierpunkt erzeugt also den Ausgang Y als Differenz von A und B.
Y = A + (-B) = A – B.
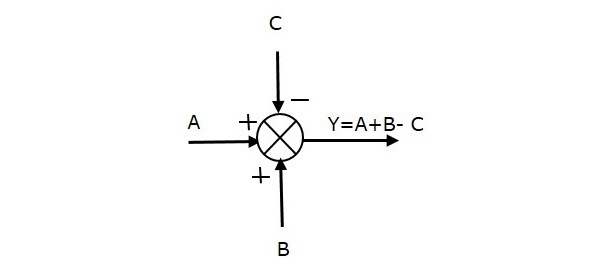
Die folgende Abbildung zeigt den Summierpunkt mit drei Eingängen (A, B, C) und einem Ausgang (Y). Hier haben die Eingänge A und B ein positives Vorzeichen und C hat ein negatives Vorzeichen. Der Summierpunkt erzeugt also den Ausgang Y als
Y = A + B + (-C) = A + B – C.
Abzweigpunkt
Der Abzweigpunkt ist ein Punkt, von dem aus das gleiche Eingangssignal durch mehr als einen Zweig geleitet werden kann. Das bedeutet, dass man mit Hilfe des Abzweigpunktes denselben Eingang an einen oder mehrere Blöcke, Summierpunkte, anlegen kann.
In der folgenden Abbildung wird der Abzweigpunkt verwendet, um denselben Eingang, R(s), an zwei weitere Blöcke anzuschließen.
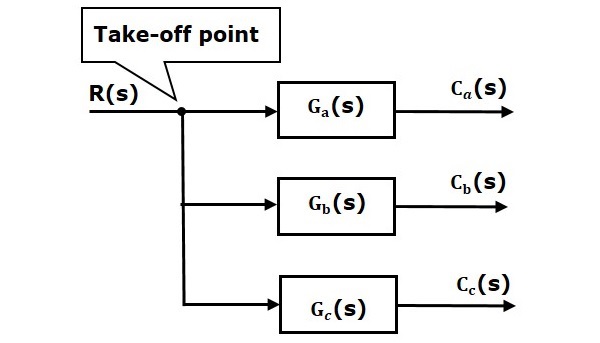
In der folgenden Abbildung wird der Abzweigpunkt verwendet, um den Ausgang C(s) als einen der Eingänge mit dem Summierpunkt zu verbinden.
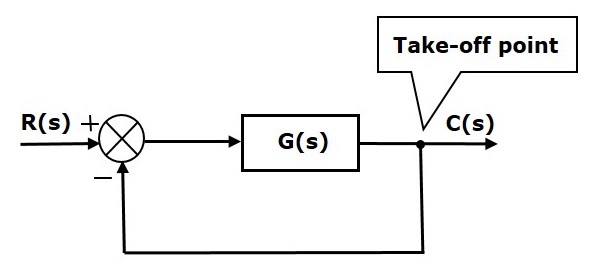
Blockdiagrammdarstellung elektrischer Systeme
In diesem Abschnitt wollen wir ein elektrisches System mit einem Blockdiagramm darstellen. Elektrische Systeme bestehen hauptsächlich aus drei Grundelementen – Widerstand, Induktivität und Kondensator.
Betrachten wir eine Reihe von RLC-Schaltungen, wie in der folgenden Abbildung dargestellt. Dabei sind Vi(t) und Vo(t) die Eingangs- und Ausgangsspannungen. i(t) sei der Strom, der durch die Schaltung fließt. Diese Schaltung befindet sich im Zeitbereich.
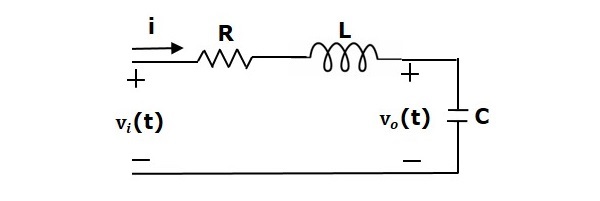
Wenn man die Laplace-Transformation auf diese Schaltung anwendet, erhält man die Schaltung im s-Bereich. Die Schaltung ist in der folgenden Abbildung dargestellt.
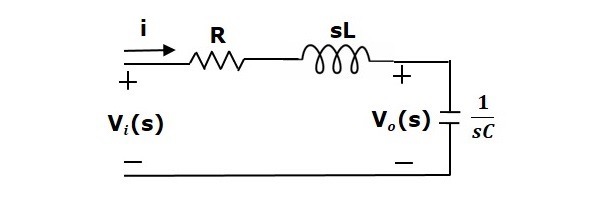
Aus der obigen Schaltung können wir schreiben
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (Gleichung 1)
$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (Gleichung 2)
Lassen Sie uns nun die Blockdiagramme für diese beiden Gleichungen einzeln zeichnen. Und dann kombinieren wir diese Blockdiagramme richtig, um das Gesamtblockdiagramm der RLC-Serienschaltung (s-Domäne) zu erhalten.
Gleichung 1 kann mit einem Block mit der Übertragungsfunktion $\frac{1}{R+sL}$ implementiert werden. Eingang und Ausgang dieses Blocks sind $\links \{ V_i(s)-V_o(s) \rechts \}$ und $I(s)$. Wir benötigen einen Summationspunkt, um $\left \{ V_i(s)-V_o(s) \right \}$ zu erhalten. Das Blockdiagramm von Gleichung 1 ist in der folgenden Abbildung dargestellt.
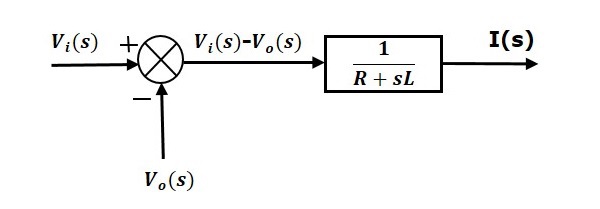
Gleichung 2 kann mit einem Block mit der Übertragungsfunktion $\frac{1}{sC}$ implementiert werden. Der Eingang und der Ausgang dieses Blocks sind $I(s)$ und $V_o(s)$. Das Blockdiagramm der Gleichung 2 ist in der folgenden Abbildung dargestellt.
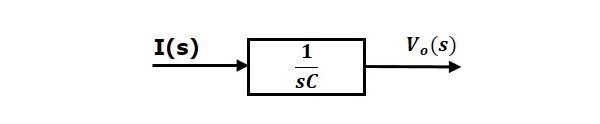
Das Gesamtblockdiagramm der RLC-Serienschaltung (s-Domäne) ist in der folgenden Abbildung dargestellt.
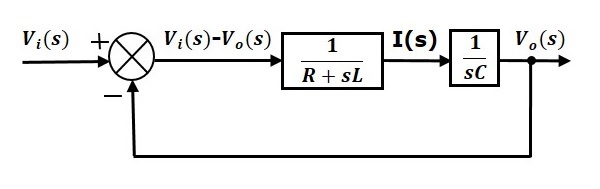
Auch das Blockdiagramm einer beliebigen elektrischen Schaltung oder eines beliebigen Systems kann mit diesem einfachen Verfahren gezeichnet werden.
-
Wandeln Sie die elektrische Schaltung im Zeitbereich durch Anwendung der Laplace-Transformation in eine elektrische Schaltung im s-Bereich um.
-
Schreiben Sie die Gleichungen für den Strom, der durch alle Reihenzweige fließt, und die Spannung an allen Nebenzweigen auf.
-
Zeichnen Sie die Blockdiagramme für alle obigen Gleichungen einzeln.
-
Kombiniere alle diese Blockdiagramme richtig, um das Gesamtblockdiagramm der elektrischen Schaltung (s-Domäne) zu erhalten.