Introducción
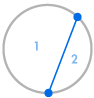
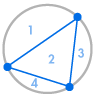
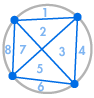
Imagina que colocamos varios puntos en la circunferencia de un círculo y conectamos cada punto entre sí. Esto divide el círculo en muchas regiones diferentes, y podemos contar el número de regiones en cada caso. Los siguientes diagramas muestran cuántas regiones hay para varios números diferentes de puntos en la circunferencia. Tenemos que asegurarnos de que sólo dos líneas se encuentran en cada intersección dentro del círculo, no tres o más.
 |
 |
 |
 |
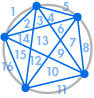 |
| 1 región | 2 regiones | 4 regiones | 8 regiones | 16 regiones |
Podemos ver inmediatamente un patrón: el número de regiones es siempre el doble del anterior, de modo que obtenemos la secuencia 1, 2, 4, 8, 16, … Esto significa que con 6 puntos en la circunferencia habría 32 regiones, y con 7 puntos habría 64 regiones.
Podemos decidir que estamos contentos con este resultado. El número de regiones es siempre el doble del anterior – después de todo esto funcionó para los primeros cinco casos. O podríamos decidir que deberíamos comprobar unas cuantas más, sólo para estar seguros:
 |
 |
| 31 regiones, no 32 | 57 regiones, no 64 |
Desgraciadamente, algo salió mal: 31 podría parecer un error de cálculo, pero 57 es mucho menos que 64. La secuencia continúa 99, 163, 256, …, muy diferente de lo que obtendríamos al duplicar el número anterior.
Este ejemplo ilustra por qué, en matemáticas, no puedes decir que una observación es siempre verdadera sólo porque funciona en unos pocos casos que has probado. En lugar de ello, hay que elaborar un argumento lógico riguroso que conduzca de los resultados que ya se conocen a algo nuevo que se quiere demostrar que es cierto. Tal argumento se llama prueba.
Las pruebas son lo que hace que las matemáticas sean diferentes de todas las demás ciencias, porque una vez que hemos demostrado algo estamos absolutamente seguros de que es y será siempre cierto. No es sólo una teoría que se ajusta a nuestras observaciones y que puede ser sustituida por una teoría mejor en el futuro.
En el ejemplo anterior, podríamos contar el número de intersecciones en el interior del círculo. Si pensamos detenidamente en la relación entre el número de intersecciones, las líneas y las regiones, acabaremos llegando a una ecuación diferente para el número de regiones cuando hay x = V.Axi puntos en el círculo:
Número de regiones = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Esta ecuación funciona en todos los casos anteriores. Ahora podríamos intentar demostrarla para cada valor de x utilizando la «inducción», una técnica que se explica más adelante.
Tradicionalmente, el final de una demostración se indica utilizando una ■ o □, o escribiendo QED o «quod erat demonstrandum», que en latín significa «lo que había que demostrar».
Un resultado o una observación que creemos que es verdadera se llama Hipótesis o Conjetura. Una vez que lo hemos demostrado, lo llamamos Teorema. Una vez que hemos demostrado un teorema, podemos utilizarlo para demostrar otros resultados más complicados – construyendo así una red creciente de teoremas matemáticos.
Axiomas

La Escuela de Atenas de Rafael: los antiguos matemáticos griegos fueron los primeros en abordar las matemáticas utilizando un marco lógico y axiomático.
Una cuestión interesante es por dónde empezar. ¿Cómo se demuestra el primer teorema, si todavía no se sabe nada? Desgraciadamente no se puede demostrar algo con nada. Necesitas al menos unos bloques de construcción para empezar, y estos se llaman Axiomas.
Los matemáticos asumen que los axiomas son verdaderos sin poder demostrarlos. Sin embargo, esto no es tan problemático como puede parecer, porque los axiomas son definiciones o claramente obvias, y sólo hay muy pocos axiomas. Por ejemplo, un axioma podría ser que a + b = b + a para dos números cualesquiera a y b.
Es importante acertar con los axiomas, porque toda la matemática se basa en ellos. Si hay muy pocos axiomas, se puede demostrar muy poco y las matemáticas no serían muy interesantes. Si hay demasiados axiomas, se puede demostrar casi cualquier cosa, y las matemáticas tampoco serían interesantes. Tampoco puedes tener axiomas que se contradigan entre sí.
Las matemáticas no consisten en elegir el conjunto correcto de axiomas, sino en desarrollar un marco de trabajo a partir de estos puntos de partida. Si empiezas con diferentes axiomas, obtendrás un tipo de matemáticas diferente, pero los argumentos lógicos serán los mismos. Cada área de las matemáticas tiene su propio conjunto de axiomas básicos.
Cuando los matemáticos han demostrado un teorema, lo publican para que otros matemáticos lo comprueben. A veces encuentran un error en el argumento lógico, y a veces no se encuentra un error hasta muchos años después. Sin embargo, en principio, siempre es posible descomponer una demostración en los axiomas básicos.
Teoría de conjuntos y el axioma de elección

Para formular las demostraciones a veces es necesario remontarse al fundamento mismo del lenguaje en el que se escriben las matemáticas: la teoría de conjuntos.
Un conjunto es una colección de objetos, como los números. Los elementos de un conjunto suelen escribirse entre corchetes. Podemos encontrar la unión de dos conjuntos (el conjunto de elementos que están en cualquiera de los dos conjuntos) o podemos encontrar la intersección de dos conjuntos (el conjunto de elementos que están en ambos conjuntos).
Muchos problemas matemáticos se pueden formular en el lenguaje de la teoría de conjuntos, y para demostrarlos necesitamos axiomas de la teoría de conjuntos. A lo largo del tiempo, los matemáticos han utilizado diferentes colecciones de axiomas, siendo los más aceptados los nueve axiomas de Zermelo-Fraenkel (ZF):
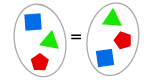
AXIOMA DE EXTENSIÓN
Si dos conjuntos tienen los mismos elementos, entonces son iguales.
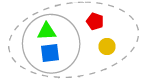
AXIOMA DE SEPARACIÓN
Podemos formar un subconjunto de un conjunto, que consta de algunos elementos.

AXIOMA DE CONJUNTO VACÍO
Hay un conjunto sin miembros, que se escribe como {} o ∅.
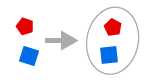
EJE DE CONJUNTO
Dados dos objetos x e y podemos formar un conjunto {x, y}.
EJE DE UNIÓN
Podemos formar la unión de dos o más conjuntos.
EJE DE CONJUNTOS DE POTENCIA
Dado un conjunto cualquiera, podemos formar el conjunto de todos los subconjuntos (el conjunto de potencia).
AXIOMA DEL INFINITO
Existe un conjunto con infinitos elementos.

AXIOMA DE FUNDACIÓN
Los conjuntos se construyen a partir de conjuntos más simples, lo que significa que todo conjunto (no vacío) tiene un miembro mínimo.
AXIOMA DE SUSTITUCIÓN
Si aplicamos una función a cada elemento de un conjunto, la respuesta sigue siendo un conjunto.
Si piensas en la teoría de conjuntos, la mayoría de estos axiomas te parecerán completamente obvios – y eso es lo que se supone que son los axiomas. Sin embargo, hay un décimo axioma que es bastante más problemático:
Axioma de elección
Dado un número infinito de conjuntos no vacíos, se puede elegir un elemento de cada uno de estos conjuntos.
A primera vista, el axioma de elección (AC) parece tan inocente como los otros anteriores. Sin embargo, el uso del infinito tiene una serie de consecuencias inesperadas. Por ejemplo, se puede utilizar el AC para demostrar que es posible cortar una esfera en cinco trozos y volver a montarlos para hacer dos esferas, cada una idéntica a la esfera inicial. Esto es sólo un concepto teórico: los cortes necesarios son fractales, lo que significa que no pueden existir en la vida real, y algunas de las piezas son «no medibles», lo que significa que no tienen un volumen definido. Pero el hecho de que el axioma de elección pueda ser utilizado para construir estos cortes imposibles es bastante preocupante.
Hay un apasionado debate entre los lógicos, si aceptar el axioma de elección o no. Cada colección de axiomas forma un pequeño «mundo matemático», y diferentes teoremas pueden ser verdaderos en diferentes mundos. En realidad es sólo una cuestión de si se está contento de vivir en un mundo en el que se pueden hacer dos esferas a partir de una…
La prueba por inducción
La prueba por inducción es una técnica que puede utilizarse para demostrar que un determinado enunciado es verdadero para todos los números naturales 1, 2, 3, … El «enunciado» suele ser una ecuación o fórmula que incluye una variable n que puede ser cualquier número natural. Denotemos el enunciado aplicado a n por S(n). He aquí los cuatro pasos de la inducción matemática:
- Primero demostramos que S(1) es verdadero, es decir, que el enunciado S es verdadero para 1.
- Ahora suponemos que S(k) es verdadero, es decir, que el enunciado S es verdadero para algún número natural k.
- Usando esta suposición, intentamos deducir que S(k + 1) también es verdadero. Así, siempre que S es verdadera para un número, también lo es para el siguiente.
- Como sabemos que S(1) es verdadera, S(2) debe serlo. Y por lo tanto S(3) debe ser verdadera. Y por lo tanto S(4) debe ser verdadera. Y así sucesivamente: S debe ser verdadera para todos los números.

La inducción puede compararse con la caída de fichas de dominó: cada vez que cae una ficha, también cae la siguiente. El primer paso, demostrar que S(1) es verdadera, inicia la reacción en cadena infinita.
El primer paso a menudo se pasa por alto, porque es muy simple. De hecho, es muy importante y toda la cadena de inducción depende de él – como mostrarán algunos de los siguientes ejemplos…
El objetivo del juego Torres de Hanoi es mover un número de discos de una clavija a otra. Sólo puedes mover un disco a la vez, y no puedes poner un disco más grande encima de otro más pequeño. Intenta mover la torre de discos desde la primera clavija hasta la última, con el menor número de movimientos posible:
Número de discos: Empezar de nuevo los movimientos: 0
Una vez que hemos entendido las reglas del juego, podemos intentar encontrar el menor número de pasos necesarios, dado cualquier número de discos. Jugando con el juego anterior podemos observar que, con n discos, se necesitan al menos 2n – 1 pasos. Llamemos a esta afirmación S(n).
S(1) es claramente cierta ya que, con un solo disco, sólo se necesita un movimiento, y 21 – 1 = 1.
Ahora supongamos que S(k) es cierta, es decir, que se necesitan 2k – 1 pasos para k discos. Entonces si tenemos k + 1 discos:
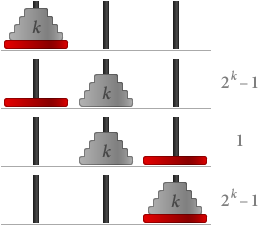
En total necesitamos (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 pasos. Esto significa que S(k + 1) también es verdadera.
Por inducción matemática, S(n) es verdadera para todos los valores de n, lo que significa que la forma más eficiente de mover n = V.Hanoi discos toma 2n – 1 = Math.pow(2,V.Hanoi)-1 movimientos. ■
Usemos la inducción para demostrar que la suma de los primeros n números naturales es n (n + 1)2. Primero comprobamos la ecuación para valores pequeños de n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
A continuación, suponemos que el resultado es cierto para k, es decir, que 1 + 2 + … + k = k (k + 1)2, donde k es algún número que no especificamos. Ahora
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Acabamos de demostrar que si la ecuación es cierta para algún k, entonces también lo es para k + 1. Por inducción matemática, la ecuación es cierta para todos los valores de n. ■
Hay otra forma inteligente de demostrar la ecuación anterior, que no utiliza la inducción. Supuestamente, Carl Friedrich Gauss (1777 – 1855), uno de los mayores matemáticos de la historia, descubrió este método en la escuela primaria, cuando su profesor le pidió que sumara todos los números enteros del 1 al 100.
Usando la inducción, queremos demostrar que todos los seres humanos tienen el mismo color de pelo. Sea S(n) la afirmación de que «cualquier grupo de n seres humanos tiene el mismo color de pelo».
Claramente S(1) es verdadera: en cualquier grupo de uno solo, todos tienen el mismo color de pelo.
Supongamos ahora S(k), que en cualquier grupo de k todos tienen el mismo color de pelo. Si sustituimos a cualquiera del grupo por otra persona, siguen siendo un total de k y, por tanto, tienen el mismo color de pelo. Esto funciona para cualquier grupo inicial de personas, lo que significa que cualquier grupo de k + 1 también tiene el mismo color de pelo. Por tanto, S(k + 1) es verdadera.
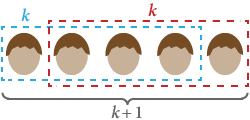
¡Por inducción matemática, todos los seres humanos tienen el mismo color de pelo! ■
Está claro que algo ha debido de fallar en la demostración anterior: al fin y al cabo, no todo el mundo tiene el mismo color de pelo. ¿Puedes encontrar el error?
Algunos teoremas no pueden demostrarse del todo usando la inducción – tenemos que usar una versión ligeramente modificada llamada Inducción Fuerte. En lugar de asumir S(k) para demostrar S(k + 1), asumimos todo S(1), S(2), … S(k) para demostrar S(k + 1). Todo lo que se puede demostrar usando la inducción (débil) puede claramente demostrarse también usando la inducción fuerte, pero no a la inversa.
El Teorema Fundamental de la Aritmética establece que todo número entero mayor que 1 es un número primo, o puede escribirse como el producto de números primos de una manera esencialmente única.
Podemos demostrar partes del mismo utilizando la inducción fuerte: dejemos que S(n) sea la afirmación de que «el número entero n es un primo o puede escribirse como el producto de números primos». S(1) es una excepción, pero S(2) es claramente verdadera porque 2 es un número primo.
Ahora supongamos que S(1), S(2), …, S(k) son todas verdaderas, para algún número entero k. Sabemos que k + 1 es un número primo o tiene factores menores que k + 1. Por nuestra suposición, sabemos que estos factores se pueden escribir como el producto de números primos. Por lo tanto, a menos que sea primo, k + 1 también puede escribirse como un producto de números primos. Esto significa que S(k + 1) es verdadera.
Por inducción fuerte, S(n) es verdadera para todos los números n mayores que 1. ■
Demostrar que esta factorización de primos es única (a no ser que se cuenten diferentes ordenaciones de los factores) requiere más trabajo, pero no es especialmente difícil.
Resulta que el principio de inducción débil y el principio de inducción fuerte son equivalentes: cada uno implica al otro. Ambos son también equivalentes a un tercer teorema, el Principio de Buen Orden: cualquier conjunto (no vacío) de números naturales tiene un elemento mínimo, más pequeño que todos los demás.
El principio de buen orden es la característica definitoria de los números naturales. Es uno de los axiomas básicos utilizados para definir los números naturales ![]() = {1, 2, 3, …}. Estos axiomas se denominan Axiomas de Peano, en honor al matemático italiano Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …}. Estos axiomas se denominan Axiomas de Peano, en honor al matemático italiano Guiseppe Peano (1858 – 1932).
Prueba por contradicción
La prueba por contradicción es otra técnica de prueba importante. Si queremos demostrar un enunciado S, suponemos que S no era verdadero. Usando esta suposición intentamos deducir un resultado falso, como 0 = 1. Si todos nuestros pasos fueron correctos y el resultado es falso, nuestra suposición inicial debe haber sido errónea. Nuestra suposición inicial era que S no es verdadera, lo que significa que S realmente es verdadera.
Esta técnica se puede utilizar en muchas circunstancias diferentes, como demostrar que √2 es irracional, demostrar que los números reales son incontables o demostrar que hay infinitos números primos.
Aquí tenemos otro ejemplo divertido:
Podemos utilizar la prueba por contradicción, junto con el principio de ordenación de pozos, para demostrar que todos los números naturales son «interesantes».
Supongamos que no todos los números naturales son interesantes, y sea S el conjunto de números no interesantes. Por el principio de ordenación del pozo, S tiene un miembro más pequeño x que es el menor número no interesante. Esta curiosa propiedad hace claramente que x sea un número especialmente interesante. Esto es una contradicción porque suponíamos que x era no interesante.
Por tanto, todos los números son interesantes. ■
Gödel y los teoremas indemostrables

Kurt Gödel (1906-1978)
A principios del siglo XX, las matemáticas comenzaron a crecer rápidamente, con miles de matemáticos trabajando en innumerables áreas nuevas. David Hilbert (1862 – 1943) puso en marcha un amplio programa para formalizar las matemáticas y resolver cualquier inconsistencia en los fundamentos de las mismas. Esto incluía demostrar todos los teoremas utilizando un conjunto de axiomas simples y universales, demostrar que este conjunto de axiomas es consistente y demostrar que este conjunto de axiomas es completo, es decir, que cualquier enunciado matemático puede ser demostrado o refutado utilizando los axiomas.
Desgraciadamente, estos planes fueron destruidos por Kurt Gödel en 1931. Demostró que en cualquier sistema matemático (suficientemente complejo) con un determinado conjunto de axiomas, se pueden encontrar algunos enunciados que no se pueden demostrar ni refutar utilizando esos axiomas. Tampoco es posible demostrar que un determinado conjunto de axiomas es consistente, utilizando nada más que los propios axiomas.
El descubrimiento de Gödel se basa en el hecho de que un conjunto de axiomas no puede utilizarse para decir nada sobre sí mismo, como por ejemplo si es consistente. Los problemas de autorreferencia no sólo se encuentran en las matemáticas, sino también en el lenguaje. He aquí la Paradoja del Mentiroso:
«Esta frase es falsa.»
La frase anterior intenta decir algo sobre sí misma. Si es verdadera, entonces la frase nos dice que es falsa. Si es falsa, entonces la frase nos dice que no es falsa, es decir, que es verdadera. En efecto, la frase no es ni verdadera ni falsa.
Cuando se publicaron por primera vez, los teoremas de Gödel preocuparon profundamente a muchos matemáticos. Cuando se intenta demostrar una observación, no se sabe si existe una prueba: el resultado podría ser verdadero pero no demostrable. Hoy sabemos que la incompletitud es una parte fundamental no sólo de la lógica, sino también de la informática, que se basa en máquinas que realizan operaciones lógicas.
Sorprendentemente, es posible demostrar que ciertas afirmaciones son indemostrables. Un ejemplo es la Hipótesis del Continuo, que trata del tamaño de los conjuntos infinitos.
Hacia el final de su vida, Kurt Gödel desarrolló graves problemas mentales y murió de inanición en 1978. Sus conocimientos sobre los fundamentos de la lógica fueron los más profundos desde el desarrollo de la prueba por los antiguos griegos.