
Bertrand Russell (1872-1970) y A.N. Whitehead (1861-1947)
Bertrand Russell y Alfred North Whitehead fueron matemáticos, lógicos y filósofos británicos, que estuvieron en la vanguardia de la revuelta británica contra el idealismo continental a principios del siglo XX y, entre ambos, hicieron importantes contribuciones en los campos de la lógica matemática y la teoría de conjuntos.
Whitehead era el mayor de los dos y procedía de una formación matemática más pura. Se convirtió en el tutor de Russell en el Trinity College de Cambridge en la década de 1890, y luego colaboró con su ex alumno más célebre en la primera década del siglo XX en su monumental obra, los «Principia Mathematica». Sin embargo, después de la Primera Guerra Mundial, que Russell pasó en gran parte en prisión debido a sus actividades pacifistas, la colaboración se apagó, y la carrera académica de Whitehead permaneció siempre a la sombra de la del más extravagante Russell. Emigró a los Estados Unidos en la década de 1920 y allí pasó el resto de su vida.
Russell nació en el seno de una familia acomodada de la aristocracia británica, aunque sus padres eran extremadamente liberales y radicales para la época. Sus padres murieron cuando Russell era bastante joven y fue criado en gran parte por su abuela, de estilo victoriano (aunque bastante progresista). Su adolescencia fue muy solitaria y sufrió ataques de depresión, afirmando más tarde que sólo su amor por las matemáticas le impidió suicidarse. Estudió matemáticas y filosofía en la Universidad de Cambridge con G.E. Moore y A.N. Whitehead, donde se convirtió en un filósofo innovador, un prolífico escritor sobre muchos temas, un ateo comprometido y un matemático y lógico inspirado. Hoy en día se le considera uno de los fundadores de la filosofía analítica, pero escribió sobre casi todas las áreas principales de la filosofía, en particular la metafísica, la ética, la epistemología, la filosofía de las matemáticas y la filosofía del lenguaje.
Russell fue un activista político comprometido y de alto nivel durante toda su larga vida. Fue un destacado activista antibélico durante la Primera y la Segunda Guerras Mundiales, defendió el libre comercio y el antiimperialismo, y más tarde se convirtió en un estridente defensor del desarme nuclear y del socialismo, y en contra de Adolf Hitler, del totalitarismo soviético y de la participación de Estados Unidos en la guerra de Vietnam.
La Paradoja de Russell
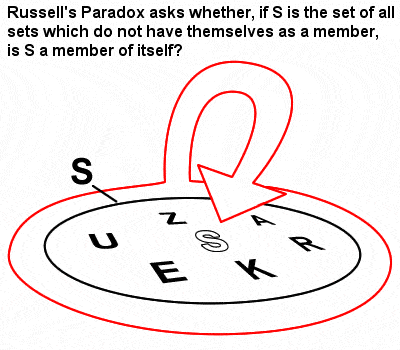
La Paradoja de Russell
Las matemáticas de Russell estuvieron muy influenciadas por la teoría de conjuntos y el logicismo que Gottlob Frege había desarrollado a raíz de los primeros e innovadores trabajos de Cantor sobre conjuntos. Sin embargo, en sus «Principios de Matemáticas» de 1903, identificó lo que ha llegado a conocerse como la Paradoja de Russell (un conjunto que contiene conjuntos que no son miembros de sí mismos), que mostraba que la ingenua teoría de conjuntos de Frege podía, de hecho, conducir a contradicciones.
La paradoja se ilustra a veces con este ejemplo simplista: «Si un barbero afeita a todos y sólo a los hombres del pueblo que no se afeitan a sí mismos, ¿se afeita a sí mismo?»
La paradoja parecía implicar que ya no se podía confiar en los propios fundamentos de toda la matemática, y que, incluso en la matemática, nunca se podría conocer la verdad de forma absoluta (los trabajos posteriores de Gödel y Turing no harían más que empeorar esto). La crítica de Russell fue suficiente para hacer tambalear la confianza de Frege en todo el edificio del logicismo, y tuvo la amabilidad de admitirlo abiertamente en un apéndice escrito a toda prisa en el volumen II de sus «Leyes básicas de la aritmética».
Pero la obra magna de Russell fue el monolítico «Principia Mathematica», publicado en tres volúmenes en 1910, 1912 y 1913. El primer volumen fue coescrito por Whitehead, aunque los dos últimos fueron casi todos obra de Russell. La aspiración de esta ambiciosa obra era nada menos que un intento de derivar toda la matemática a partir de axiomas puramente lógicos, evitando al mismo tiempo los tipos de paradojas y contradicciones que se encontraban en el trabajo anterior de Frege sobre la teoría de conjuntos. Russell lo consiguió empleando una teoría o sistema de «tipos», según el cual cada entidad matemática se asigna a un tipo dentro de una jerarquía de tipos, de modo que los objetos de un tipo determinado se construyen exclusivamente a partir de objetos de tipos precedentes más bajos en la jerarquía, evitando así los bucles. Cada conjunto de elementos, pues, es de un tipo diferente al de cada uno de sus elementos, de modo que no se puede hablar del «conjunto de todos los conjuntos» y construcciones similares, que conducen a paradojas.
Sin embargo, los «Principia» requerían, además de los axiomas básicos de la teoría de tipos, tres axiomas más que parecían no ser verdaderos como meras cuestiones de lógica, a saber, el «axioma del infinito» (que garantiza la existencia de al menos un conjunto infinito, a saber, el conjunto de todos los números naturales), el «axioma de la elección» (que asegura que, dada cualquier colección de «recipientes», cada uno de los cuales contiene al menos un objeto, es posible hacer una selección de exactamente un objeto de cada recipiente, incluso si hay infinitamente muchos recipientes, y que no hay ninguna «regla» para qué objeto elegir de cada uno) y el propio «axioma de reducibilidad» de Russell (que establece que cualquier función de verdad proposicional puede ser expresada por una función de verdad predicativa formalmente equivalente).
Durante los aproximadamente diez años que Russell y Whitehead dedicaron a los «Principia», se iniciaron y abandonaron borradores tras borradores, ya que Russell se replanteaba constantemente sus premisas básicas. Russell y su esposa Alys incluso se mudaron a casa de los Whitehead para acelerar el trabajo, aunque su propio matrimonio se resintió cuando Russell se encaprichó de la joven esposa de Whitehead, Evelyn. Finalmente, Whitehead insistió en la publicación de la obra, aunque no estuviera (y tal vez nunca lo estuviera) completa, aunque se vieron obligados a publicarla a sus expensas, ya que ninguna editorial comercial quería tocarla.
Principia Mathematica

Una pequeña parte de la larga prueba de que 1+1 =2 en los «Principia Mathematica»
Una idea del alcance y la exhaustividad de los «Principia» puede deducirse del hecho de que se necesitan más de 360 páginas para demostrar definitivamente que 1 + 1 = 2.
Hoy en día, es ampliamente considerado como uno de los trabajos más importantes y seminales en lógica desde el «Organon» de Aristóteles. Parece que tuvo un notable éxito y resistencia en sus ambiciosos objetivos, y pronto ganó fama mundial para Russell y Whitehead. De hecho, sólo el teorema de incompletitud de Gödel de 1931 demostró finalmente que los «Principia» no podían ser a la vez consistentes y completos.
Russell recibió la Orden del Mérito en 1949 y el Premio Nobel de Literatura al año siguiente. Su fama siguió creciendo, incluso fuera de los círculos académicos, y se convirtió en una especie de nombre familiar en su vida posterior, aunque en gran medida como resultado de sus contribuciones filosóficas y su activismo político y social, que continuó hasta el final de su larga vida. Murió de gripe en su querida Gales a la avanzada edad de 97 años.
| << Volver a Hardy y Ramanujan | Adelante con Hilbert >> |