¿Qué es un Entramado?
Un entramado es un conjunto ordenado de puntos que describe la disposición de las partículas que forman un cristal.
La celda unitaria de un cristal está definida por los puntos del entramado.La celda unitaria es la parte más pequeña de un cristal que repetida regularmente por traslación en tres dimensiones crea el cristal completo.
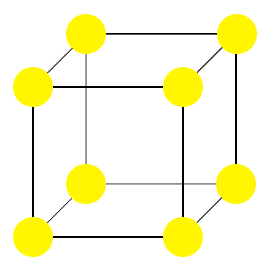
Por ejemplo, la imagen mostrada aquí es la celda unitaria de una estructura cúbica primitiva.
En la estructura dibujada, todas las partículas (amarillas) son iguales.En este caso particular, los puntos de la red que definen la celda unitaria coinciden con los centros de las partículas del cristal. Esto no tiene por qué ser siempre así.
La red iónica
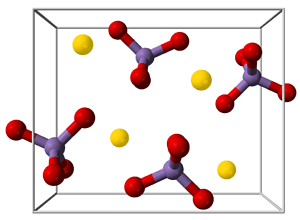
Si un cristal está formado por iones, el compuesto puede describirse como una red iónica.
Ejemplos bien conocidos de retículas iónicas son el cloruro de sodio, el permanganato de potasio, el bórax (borato de sodio) y el sulfato de cobre(II).

La red covalente
Si un cristal está formado por átomos unidos covalentemente, puede describirse como una red covalente o red covalente infinita.
Ejemplos bien conocidos de redes covalentes son el diamante, el cuarzo (dióxido de silicio), el silicio y el estaño gris.
Constantes de red
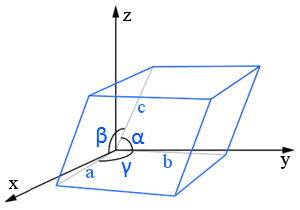
Las constantes de red (o parámetros de red) son las longitudes y los ángulos entre de los bordes de la celda unidad.
En este diagrama de celosía de paralelepípedo, las constantes de celosía son a, b y c (longitudes) y α, β y γ (ángulos).
Estructuras de celosía
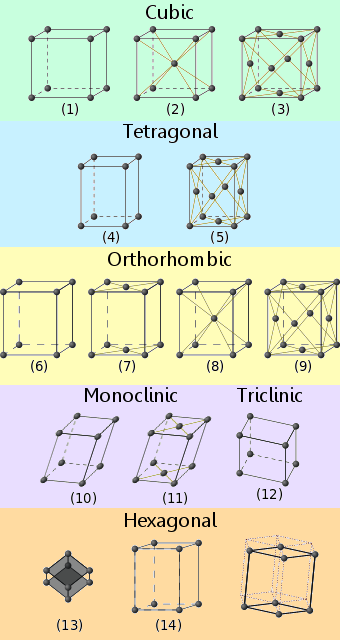
Los materiales cristalinos se ajustan a una de las catorce disposiciones de red reconocidas.Se conocen como redes de Bravais.
Los nombres de los sistemas de red cristalina, correspondientes a los números de los diagramas, son los siguientes:
1. Cúbico primitivo
2. Cúbico centrado en el cuerpo
3. Cúbico centrado en la cara
4. Tetragonal primitivo
5. Tetragonal centrado en el cuerpo
6. Ortorrómbico primitivo
7. Ortorrómbico centrado en la base
8. Ortorrómbico centrado en el cuerpo
9. Ortorrómbico centrado en la cara
10. Monoclínico primitivo
11. Monoclínico centrado en la base
12. Triclínico
13. Romboédrica
14. Hexagonal
Defectos de la red
Si se supusiera que un cristal se basa en una red iónica matemáticamente perfecta, su resistencia a la tracción calculada sería mucho mayor que la que se observa en realidad.