El método Delta-Delta Ct o método Livak es el método preferido para el análisis de datos de qPCR. Sin embargo, sólo puede utilizarse cuando se cumplen ciertos criterios. Si no es así, el método más generalizado es el de Pfaffl. Por favor, lea el material de lectura adicional para obtener más información sobre este método.
Aquí están los pasos para el método de Livak:
El archivo de Excel con todos los cálculos están en la carpeta de análisis qPCR en Blackboard.
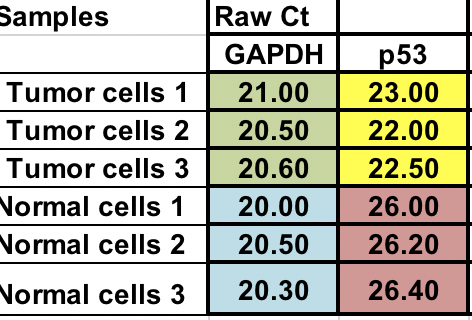
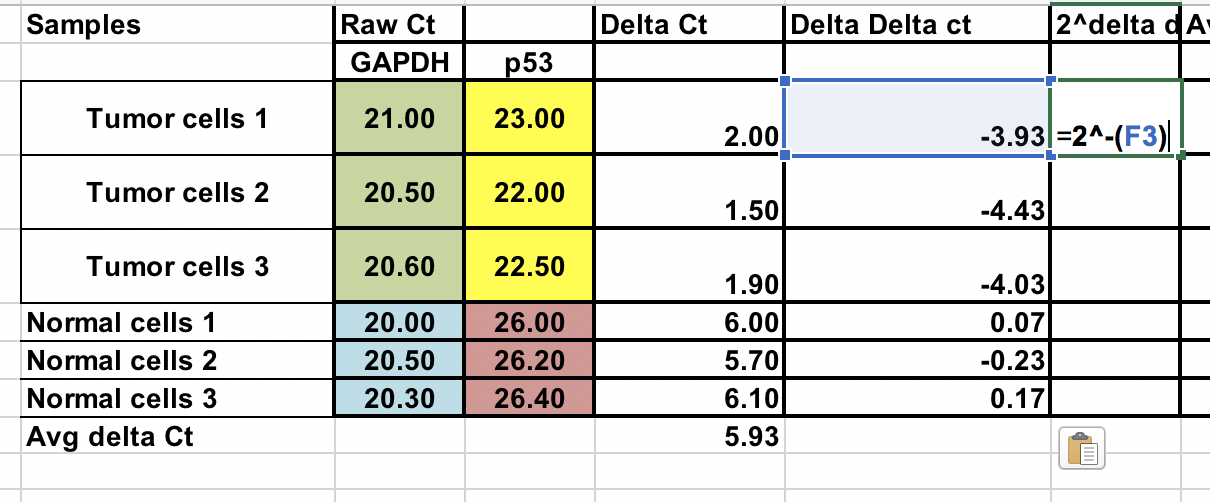
Tienes el Ct bruto (número de ciclos que se necesitan para alcanzar el umbral) para las células normales y tumorales (3 réplicas para cada una).
Normalización¶
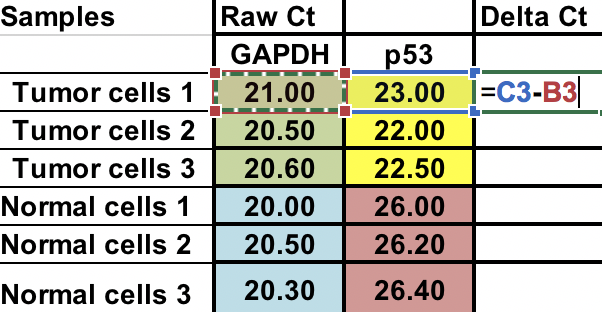
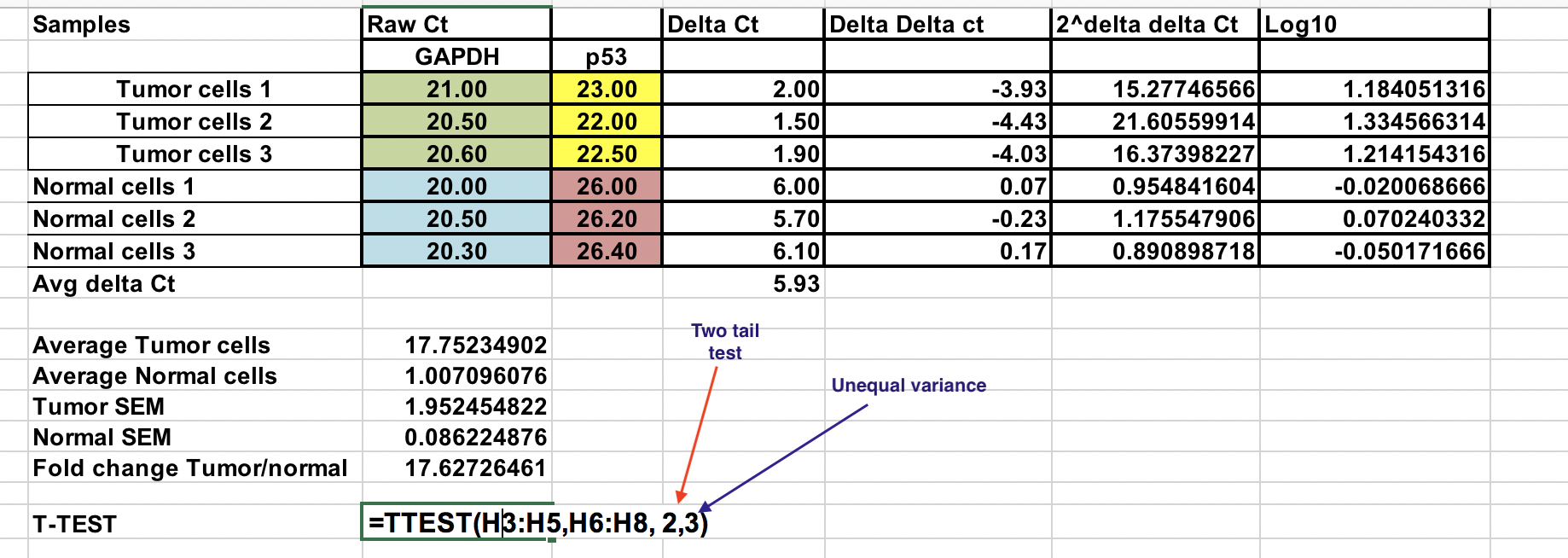
Primero, necesitarás calcular la diferencia relativa entre el gen de interés (p53) y el gen de mantenimiento (GAPDH).
∆Ct = Ct (gen de interés) – Ct (gen de mantenimiento)
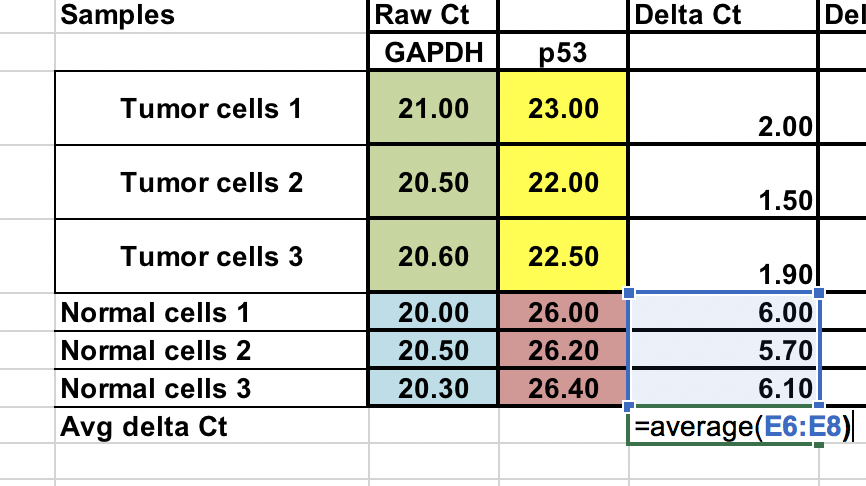
Promedio de las muestras de control (células normales)¶
Como comparamos nuestro tumor (tratamiento) con el control (células normales), primero tenemos que promediar el ∆Ct de las 3 muestras de control (normales).
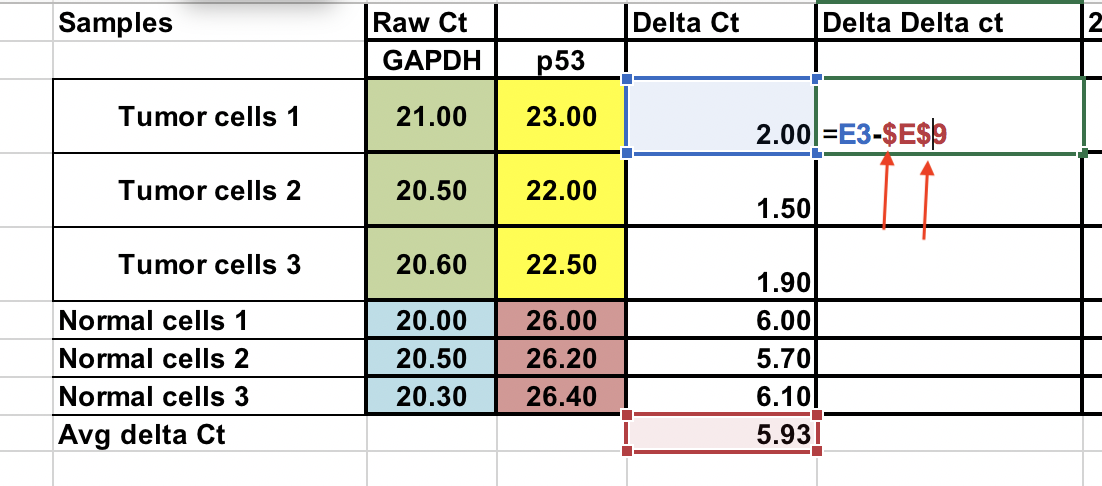
Calcule el ∆∆Ct relativo a la media del ∆Ct de las células normales células¶
∆∆Ct = ∆Ct (muestra de tumor) – ∆Ct (promedio normal)
También puede hacer esto muestras normales. Utilice los signos $ delante del número de columna y la letra cruda (flechas) para fijar la celda.
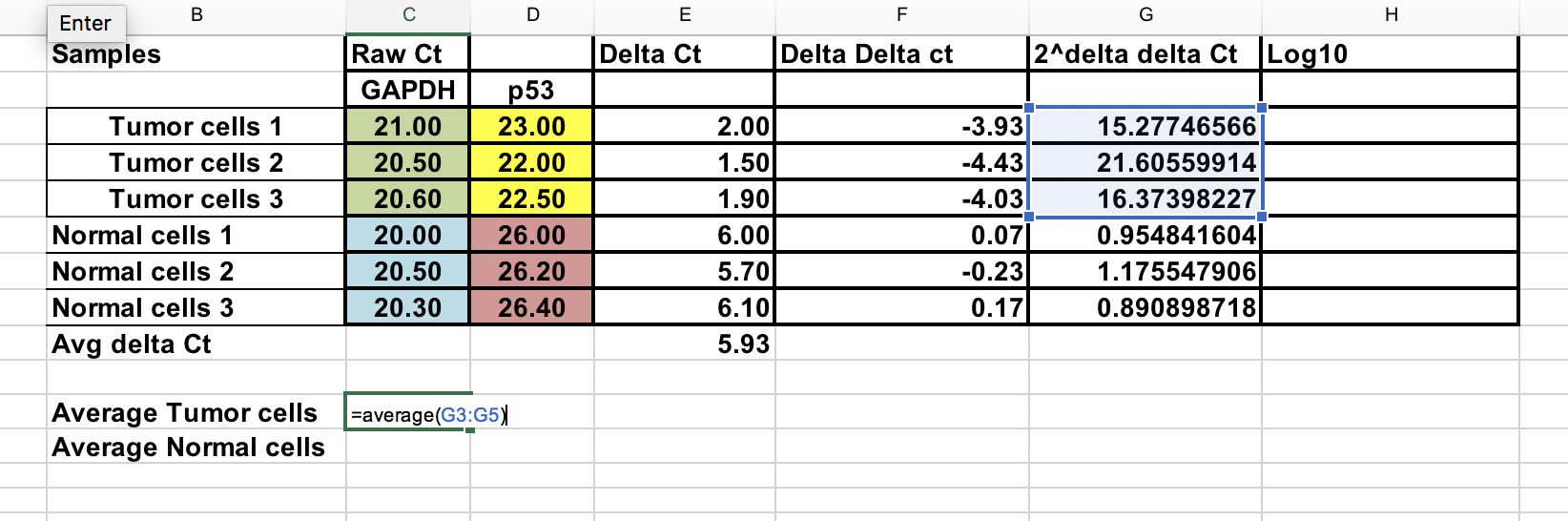
Doblar la expresión génica para cada muestra¶
Asegúrese de elevar el ∆∆Ct negativo a la potencia de dos.
Expresión génica en pliegues = 2^-(∆∆Ct)
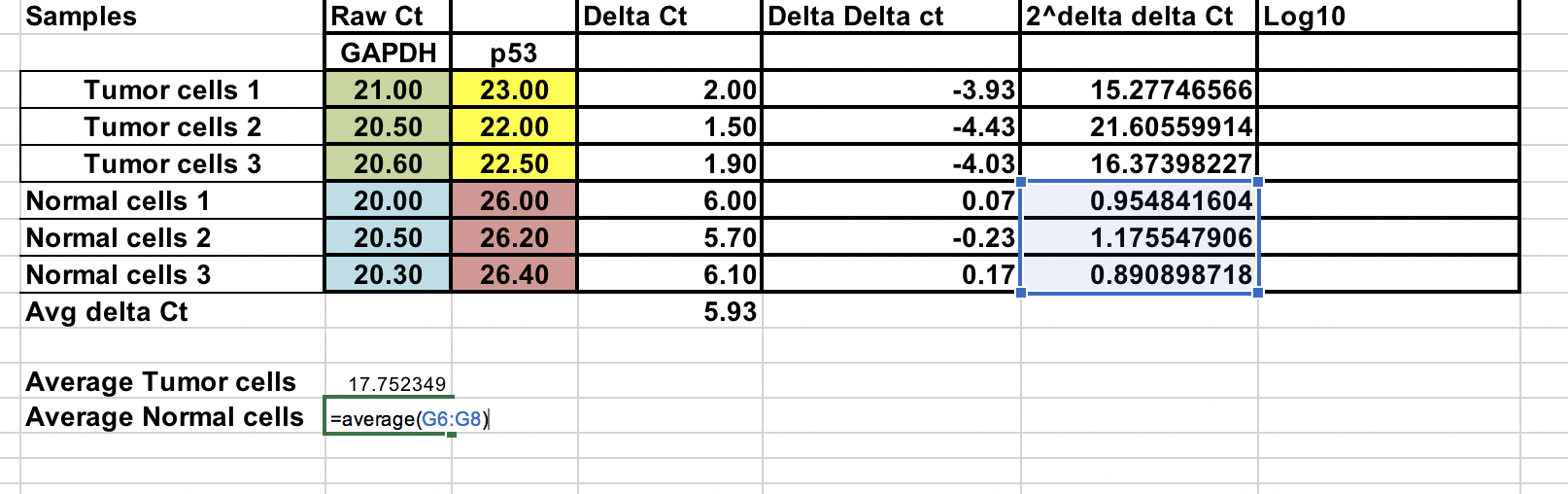
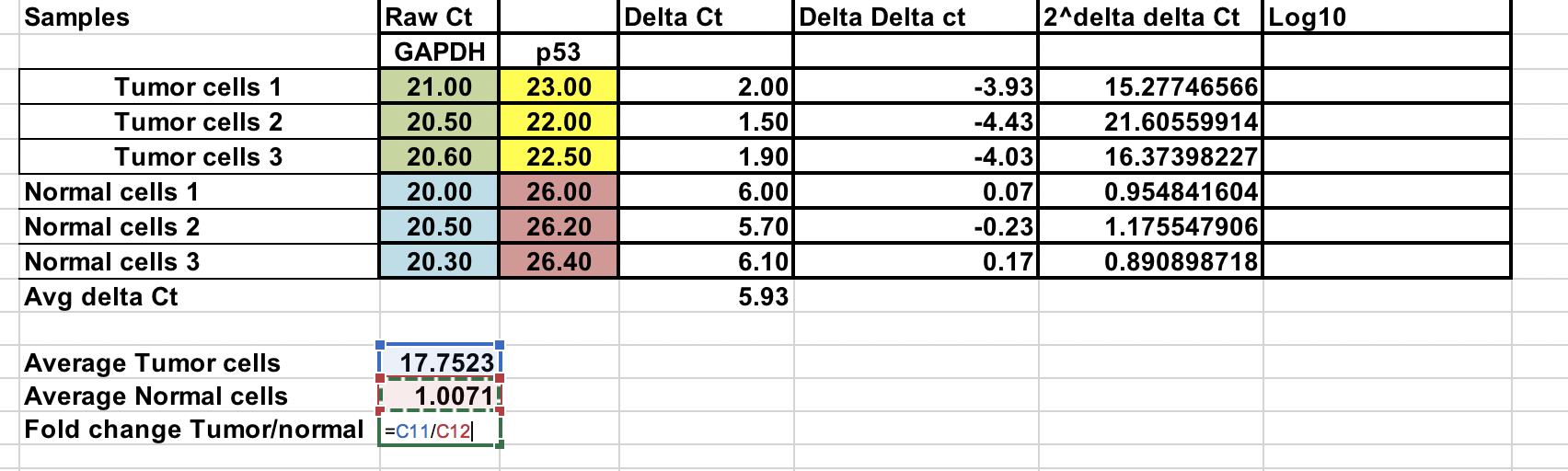
Cambio de pliegues global¶
Puede calcular el cambio de pliegues medio para las muestras tumorales y normales. La relación entre estos dos es el cambio de pliegue entre el tumor y las muestras normales.
Transformación logarítmica¶
Para realizar pruebas estadísticas paramétricas como la prueba T, se aconseja transformar los resultados finales de la expresión génica a valores logarítmicos (cualquier base logarítmica). Esto haría que la distribución de los datos fuera simétrica.
Aquí hemos cambiado el 2^-(∆∆Ct) a log 10.
T-test¶
Hay que tener cuidado cuando se utilizan pruebas paramétricas si los datos no se distribuyen normalmente, ya que llevaría a conclusiones erróneas.
Seleccione el log 10 de los valores de 2^-(∆∆Ct) para las muestras normales y tumorales como se indica. Utilice la prueba de dos colas (número 2) y asuma una varianza desigual (3).
El valor P resultante es inferior a 0,05 y, por tanto, rechazamos la hipótesis nula y las dos medias muestrales son significativamente diferentes al nivel 0,05.
.