16.3 Estrategias mixtas
Objetivo de aprendizaje
- ¿Qué juegos requieren o admiten la aleatorización como parte de su solución?
Consideremos de nuevo el juego de emparejar monedas de un centavo, como se ilustra en la figura 16.Figura 16.13 «Emparejando peniques de nuevo».
Supongamos que Fila cree que Columna juega Cara con probabilidad p. Entonces si Fila juega Cara, Fila obtiene 1 con probabilidad p y -1 con probabilidad (1 – p), para un valor esperado de 2p – 1. Del mismo modo, si la fila juega a cruz, obtiene -1 con probabilidad p (cuando la columna juega a cara) y 1 con probabilidad (1 – p), para un valor esperado de 1 – 2p. Esto se resume en la Figura 16.14 «Estrategia mixta en el emparejamiento de peniques».
Si 2p – 1 > 1 – 2p, entonces a Fila le conviene, en promedio, jugar a Cara que a Cruz. Del mismo modo, si 2p – 1 < 1 – 2p, entonces Row está mejor jugando a Cruz que a Cara. Si, por el contrario, 2p – 1 = 1 – 2p, entonces Row obtiene la misma recompensa sin importar lo que haga. En este caso, Row podría jugar a Cara, podría jugar a Cruz, o podría lanzar una moneda y aleatorizar el juego de Row.
Un equilibrio de Nash de estrategia mixtaUn equilibrio de Nash en el que al menos un jugador juega una estrategia aleatoria y ningún jugador puede aumentar su resultado esperado jugando una estrategia alternativa. implica que al menos un jugador juega una estrategia aleatoria y ningún jugador puede aumentar su resultado esperado jugando una estrategia alternativa. Un equilibrio de Nash en el que ningún jugador juega al azar se denomina equilibrio de Nash de estrategia puraUn equilibrio de Nash en el que ningún jugador juega al azar..
Figura 16.14 Estrategia mixta en el emparejamiento de peniques
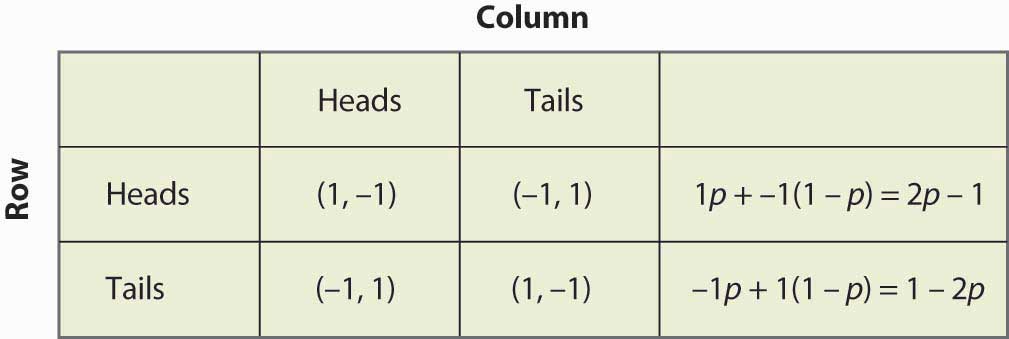
Nótese que la aleatorización requiere la igualdad de los pagos esperados. Si un jugador debe aleatorizar sobre la estrategia A o la estrategia B, entonces ambas estrategias deben producir el mismo pago esperado. De lo contrario, el jugador preferiría una de ellas y no jugaría la otra.
El cálculo de una estrategia mixta tiene un elemento que a menudo parece confuso. Supongamos que Row va a jugar al azar. Entonces los pagos de Row deben ser iguales para todas las estrategias que Row juegue con probabilidad positiva. Pero esa igualdad en los resultados de Row no determina las probabilidades con las que Row juega las distintas filas. En cambio, esa igualdad en los pagos de Row determinará las probabilidades con las que Column juega las distintas columnas. La razón es que son las probabilidades de la Columna las que determinan los pagos esperados para la Fila; si la Fila va a jugar al azar, entonces las probabilidades de la Columna deben ser tales que la Fila esté dispuesta a jugar al azar.
Así, por ejemplo, calculamos el pago para la Fila de jugar Cara, que era 2p – 1, donde p era la probabilidad de que la Columna jugara Cara. Del mismo modo, la recompensa para Row de jugar a Cruz era 1 – 2p. Row está dispuesto a jugar al azar si estos son iguales, lo que resuelve para p = ½.
Ahora vamos a intentar un ejemplo algo más desafiante y volver a la batalla de los sexos. La figura 16.15 «Estrategia mixta en la batalla de los sexos» ilustra los pagos una vez más.
Figura 16.15 Estrategia mixta en la batalla de los sexos
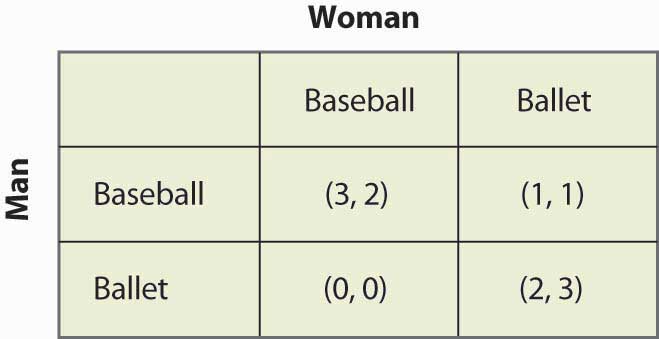
Este juego tiene dos equilibrios de Nash de estrategia pura: (Béisbol, béisbol) y (Ballet, ballet). ¿Existe una estrategia mixta? Para calcular una estrategia mixta, deje que la mujer vaya al juego de béisbol con probabilidad p, y que el hombre vaya al juego de béisbol con probabilidad q. La figura 16.16 «Cálculo completo de la estrategia mixta» contiene el cálculo de los resultados de la estrategia mixta para cada jugador.
Figura 16.16 Cálculo completo de la estrategia mixta
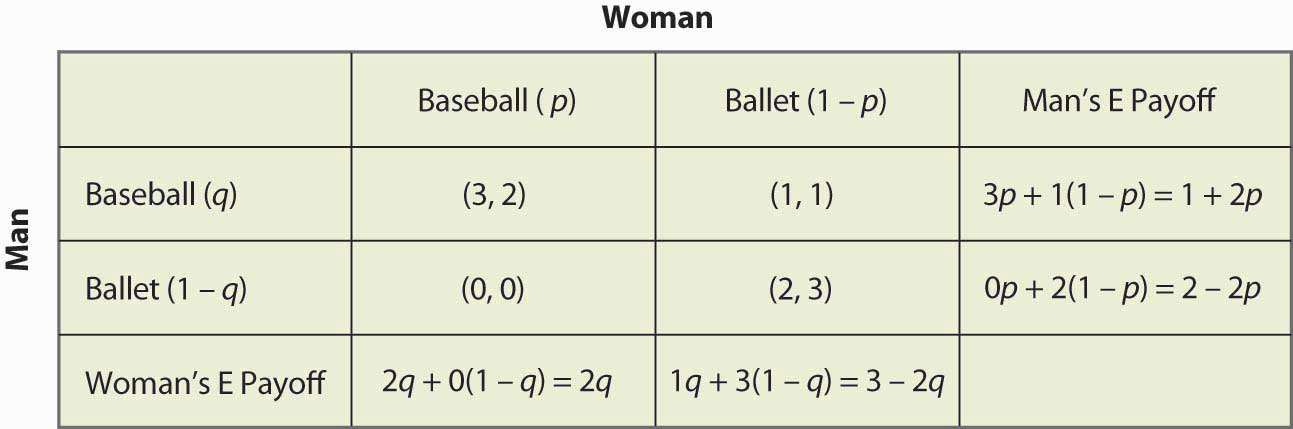
Por ejemplo, si el Hombre (jugador de la fila) va al juego de Béisbol, obtiene 3 cuando la Mujer va al juego de Béisbol (probabilidad p), y en caso contrario obtiene 1, para un pago esperado de 3p + 1(1 – p) = 1 + 2p. Los otros cálculos son similares, pero definitivamente debe correr a través de la lógica y verificar cada cálculo.
Una estrategia mixta en el juego de la batalla de los sexos requiere que ambas partes al azar (ya que una estrategia pura por cualquiera de las partes impide la aleatorización por el otro). La indiferencia del Hombre entre ir al juego de Béisbol y al Ballet requiere 1 + 2p = 2 – 2p, lo que arroja p = ¼. Es decir, el Hombre estará dispuesto a elegir al azar el evento al que asiste si la Mujer va al Ballet ¾ de las veces, y en caso contrario al partido de Béisbol. Esto hace que el Hombre sea indiferente entre los dos eventos porque prefiere estar con la Mujer, pero también le gusta estar en el partido de Béisbol. Para compensar la ventaja que el juego tiene para él, la Mujer tiene que estar en el Ballet más a menudo.
De manera similar, para que la Mujer se aleatorice, la Mujer debe obtener iguales recompensas por ir al juego de Béisbol e ir al Ballet, lo que requiere 2q = 3 – 2q, o q = ¾. Así, la probabilidad de que el hombre vaya al partido de béisbol es ¾, y va al ballet ¼ de las veces. Son probabilidades independientes, por lo que para obtener la probabilidad de que ambos vayan al partido de béisbol, multiplicamos las probabilidades, lo que da como resultado 3/16. La figura 16.17 «Probabilidades de estrategia mixta» rellena las probabilidades de los cuatro resultados posibles.
Figura 16.17 Probabilidades de estrategia mixta
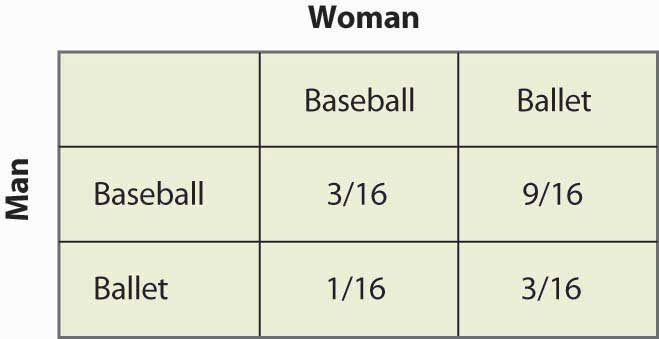
Nótese que más de la mitad de las veces (Béisbol, Ballet) es el resultado de la estrategia mixta y las dos personas no están juntas. Esta falta de coordinación es generalmente una característica de los equilibrios de estrategia mixta. Los resultados esperados de ambos jugadores también se pueden calcular fácilmente. La recompensa del hombre es 1 + 2p = 2 – 2p, y como p = ¼, el hombre obtiene 1½. Un cálculo similar muestra que la recompensa de la mujer es la misma. Por lo tanto, a ambos les va peor que coordinar su resultado menos preferido. Pero este equilibrio de Nash de estrategia mixta, por indeseable que parezca, es un equilibrio de Nash en el sentido de que ninguna de las partes puede mejorar su propia retribución, dado el comportamiento de la otra parte.
En la batalla de los sexos, el equilibrio de Nash de estrategia mixta puede parecer improbable; y podríamos esperar que la pareja se coordinara más eficazmente. De hecho, una simple llamada telefónica debería descartar la estrategia mixta. Así que consideremos otro juego relacionado con la batalla de los sexos, en el que un fallo de coordinación tiene más sentido. Se trata del juego de la «gallina». En este juego, dos jugadores conducen el uno hacia el otro, tratando de convencer al otro de que ceda el paso y finalmente se desvíe hacia una zanja. Si ambos se desvían hacia la zanja, el resultado es un empate y ambos obtienen un cero. Si uno se desvía y el otro no, el conductor que se desvía pierde y el otro gana, y le damos un punto al ganador. Por lo tanto, siempre podemos dejar que un resultado para cada jugador sea cero, y otro resultado sea uno. La única cuestión que queda por resolver es qué ocurre cuando ninguno de los dos rinde, en cuyo caso se produce un choque. En esta versión, el pago se ha fijado en cuatro veces la pérdida por desviarse, como se muestra en la figura 16.18 «Pollo», pero se puede cambiar el juego y ver qué ocurre.
Figura 16.18 Pollo
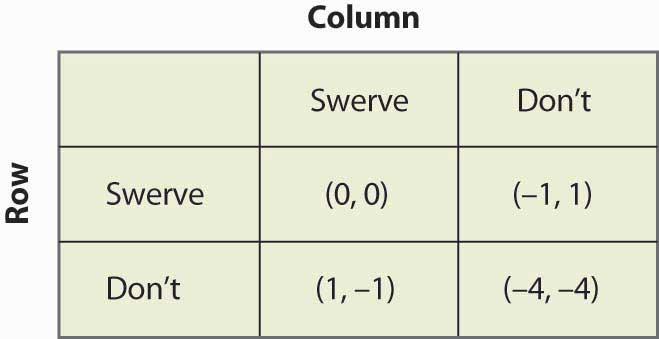
Este juego tiene dos equilibrios de estrategia pura: (Desviarse, No) y (No, Desviarse). Además, tiene una estrategia mixta. Supongamos que la Columna se desvía con probabilidad p. Entonces la Fila obtiene 0p + -1(1 – p) de desviarse, 1p + (-4)(1 – p) de no desviarse, y la Fila se aleatorizará si son iguales, lo que requiere p = ¾. Es decir, la probabilidad de que Columna se desvíe en un equilibrio de estrategia mixta es ¾. Se puede verificar que el jugador de la fila tiene la misma probabilidad estableciendo la probabilidad de que la fila se desvíe igual a q y calculando los resultados esperados de la columna. Por tanto, la probabilidad de colisión es de 1/16 en el equilibrio de estrategia mixta.
El equilibrio de estrategia mixta es más probable, en cierto sentido, en este juego: Si los jugadores ya supieran quién va a ceder, no necesitarían jugar el juego. El objetivo del juego es averiguar quién va a ceder, lo que significa que no se sabe de antemano. Esto significa que el equilibrio de estrategia mixta es, en cierto sentido, el equilibrio más razonable.
Figura 16.19 Piedra, papel o tijera
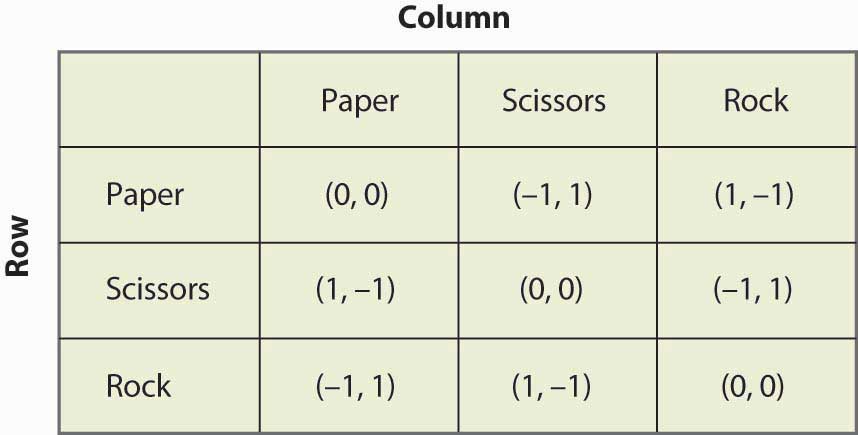
«Piedra, papel o tijera» es un juego infantil en el que dos niños utilizan sus manos para elegir simultáneamente papel (mano plana), tijera (mano con dos dedos que sobresalen para que parezca una tijera) o piedra (mano cerrada en un puño). La naturaleza de los resultados es que el papel gana a la piedra, la piedra gana a las tijeras y las tijeras ganan al papel. Este juego tiene la estructura que se ilustra en la figura 16.19 «Piedra, papel y tijera».
Consignas clave
- Un equilibrio de Nash de estrategia mixta implica que al menos un jugador juegue una estrategia aleatoria y que ningún jugador pueda aumentar su resultado esperado jugando una estrategia alternativa.
- Un equilibrio de Nash sin aleatorización se llama equilibrio de Nash de estrategia pura.
- Si se supone que un jugador aleatoriza sobre dos estrategias, entonces ambas deben producir el mismo pago esperado.
- El juego de emparejar centavos tiene una estrategia mixta y ninguna estrategia pura.
- El juego de la batalla de los sexos tiene una estrategia mixta y dos estrategias puras.
- El juego del pollo es similar al de la batalla de los sexos y, al igual que éste, tiene dos estrategias puras y una estrategia mixta.
Ejercicios
- Sea q la probabilidad de que Fila juegue a Cara. Demuestre que Columna está dispuesta a jugar al azar, si y sólo si q = ½. (Sugerencia: Primero calcule la ganancia esperada de la Columna cuando juega Cara, y luego calcule la ganancia esperada de la Columna cuando juega Cruz. Estos deben ser iguales para que Columna se aleatorice.)
- Demuestre que en el juego de piedra, papel y tijera no hay equilibrios de estrategia pura. Demuestre que jugar las tres acciones con igual probabilidad es un equilibrio de estrategia mixta.
-
Encuentre todos los equilibrios de los siguientes juegos:
Figura 16.20
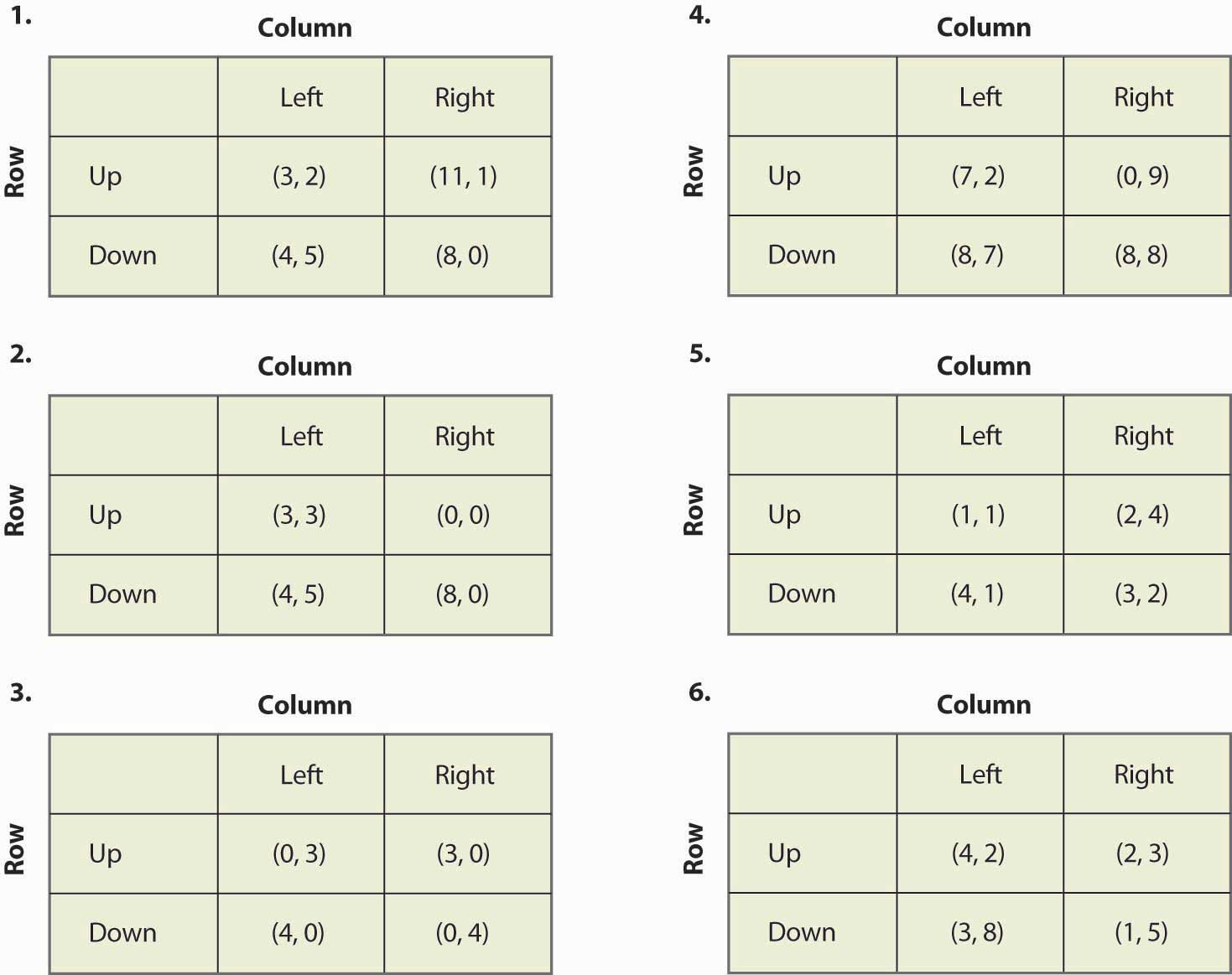
- Si se multiplica el pago de un jugador por una constante positiva, los equilibrios del juego no cambian. ¿Es esto cierto o falso, y por qué?