Hablar en tres dimensiones

Mira esta imagen de un prisma rectangular:

¿Cuántos vértices tiene? 8

¿Cuántas aristas? 12

¿Cuántas caras? 6

Fácil, ¿no?

Intentemos otra. Mira esta imagen de un cono:

¿Cuántos vértices tiene? ¿Cuenta el punto de arriba?

¿Cuántas aristas? Hmm, no estoy seguro. ¿No se supone que las aristas son rectas?

¿Cuántas caras? Eso es fácil. Una. Hay una cara circular en la parte inferior. Pero eso no es un polígono, así que ¿sigue siendo una cara? Ah, ¿y cómo llamo a la otra superficie del cono? ¿Las caras no tienen que ser planas?

Una pregunta habitual que recibimos de los profesores de 1º, 2º y 3º curso tiene que ver con cómo describir los atributos de ciertos sólidos tridimensionales, concretamente los cilindros y los conos. Según el TEKS, los alumnos deben describir los sólidos tridimensionales utilizando un lenguaje geométrico formal como vértice, arista y cara. El problema es que estamos intentando utilizar un lenguaje que funciona para una clase de formas para describir los atributos de una clase completamente diferente.

Las formas tridimensionales como los prismas y las pirámides son poliedros. «En geometría un poliedro es simplemente un sólido tridimensional que consiste en un conjunto de polígonos, normalmente unidos por sus aristas». (Fuente) Estos sólidos tienen «caras poligonales planas, aristas rectas y comparten esquinas o vértices.» (Fuente)

Las esferas, los cilindros y los conos, en cambio, no son poliedros. Como resultado, no podemos usar exactamente el mismo lenguaje para describirlos, o si usamos el mismo lenguaje es con el entendimiento de que las definiciones no son idénticas. Tomemos la palabra vértice, por ejemplo.

En un prisma rectangular, un vértice es el punto agudo o la esquina donde se encuentran las aristas. Un prisma rectangular tiene 8 vértices.

Sin embargo, este mismo término puede utilizarse también para describir la punta de un cono. El mismo término, pero no la misma definición. Como dice el Dr. Math,

La parte realmente complicada aquí es que el «vértice» de un cono no tiene nada que ver con las aristas, por lo que necesita una definición totalmente nueva; y no se me ocurre una definición realmente buena de nivel elemental para lo que obviamente quieren decir, que es simplemente un «punto».

Cuando los estudiantes sigan con matemáticas más avanzadas, podrán desarrollar un lenguaje y unas definiciones más sofisticadas. Mientras tanto, mientras están en la escuela primaria, utilizamos el término vértice de un cono en RRISD para describir este atributo de un cono.

Si queremos que los estudiantes describan y clasifiquen este tipo de sólido tridimensional, entonces tenemos que proporcionar un lenguaje accesible para ese propósito.

¿Y qué pasa con los otros atributos de un cono? De nuevo, nuestro objetivo es proporcionar un lenguaje accesible para los estudiantes de primaria y descriptivo de estos atributos, reconociendo que nuestros estudiantes desarrollarán una comprensión más formal más adelante en sus carreras escolares. Para describir un cono, diremos que tiene una base circular, la superficie plana sobre la que se apoya el cono. También decimos que tiene una arista curva a lo largo de la base y una superficie curva que se extiende desde esta arista hasta el vértice.

¿Y un cilindro? Ahora que tenemos un lenguaje accesible para describir los atributos de un cono, podemos extender este lenguaje para describir los atributos de los cilindros.

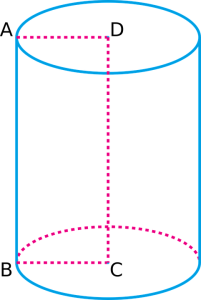
El cilindro anterior está compuesto por dos bases circulares, una en la parte superior y otra en la inferior. También tiene dos aristas curvas, una en la parte superior y otra en la inferior. Por último, tiene una superficie curva que se extiende desde la arista inferior hasta la arista superior.

Debo añadir que tanto el cono como el cilindro que he descrito son un cono circular recto y un cilindro recto. Al igual que con los polígonos y los poliedros, hay muchos otros tipos de ejemplos de estas formas. Por ejemplo, el cono o el cilindro pueden inclinarse, haciéndolos oblicuos.

Es importante que los estudiantes vean una variedad de ejemplos de figuras bidimensionales y tridimensionales. Cuantos más encuentren, más tendrán que enfrentarse a sus definiciones y a su terminología, lo que sirve para reforzar su comprensión de los atributos y de cómo nos ayudan a identificar y clasificar estas figuras.

¿Y cómo se ve esto en el STAAR?

En el examen publicado en 2016, el STAAR hizo una pregunta que abordaba este mismo tema y reforzaba el vocabulario que estamos utilizando en RRISD.

La respuesta correcta es F No tienen vértices. Si te fijas en el conjunto B, te darás cuenta de que incluye un cono, que como hemos comentado antes sí tiene un vértice. Si la Agencia de Educación de Texas no utilizara el término vértice de un cono, entonces probablemente habríamos visto el cono incluido en el conjunto A.

Aquí tienes un pensamiento de despedida del Dr. Math:

La definición que utilices depende de lo que vayas a hacer con ella. Si sólo estás describiendo objetos, mi definición suelta está bien. Si vas a demostrar teoremas que implican planos y ángulos, querrás limitarte a la definición poligonal, pero entonces no harás preguntas sobre conos. Creo que la gente a menudo no se da cuenta de que, aunque seamos exigentes con las definiciones en matemáticas, éstas varían de un campo a otro, ya que se adaptan a un determinado contexto. Eso es lo que intento hacer aquí.