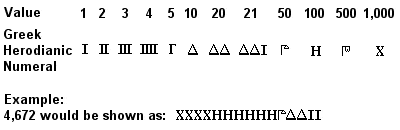
Antiguos números griegos herodianos
Cuando el imperio griego comenzó a extender su esfera de influencia en Asia Menor, Mesopotamia y más allá, los griegos fueron lo suficientemente inteligentes como para adoptar y adaptar elementos útiles de las sociedades que conquistaron. Esto fue tan cierto para sus matemáticas como para cualquier otra cosa, y adoptaron elementos matemáticos tanto de los babilonios como de los egipcios. Pero pronto empezaron a hacer importantes aportaciones por derecho propio y, por primera vez, podemos reconocer las contribuciones individuales. Para el período helenístico, los griegos habían presidido una de las revoluciones más dramáticas e importantes en el pensamiento matemático de todos los tiempos.
Números áticos o herodianos
El antiguo sistema numérico griego, conocido como números áticos o herodianos, estaba completamente desarrollado hacia el 450 a.C., y en uso regular posiblemente ya en el siglo VII a.C.. Era un sistema de base 10 similar al egipcio anterior (y aún más similar al sistema romano posterior), con símbolos para 1, 5, 10, 50, 100, 500 y 1.000 repetidos tantas veces como fuera necesario para representar el número deseado. La adición se hacía sumando por separado los símbolos (1s, 10s, 100s, etc) de los números a sumar, y la multiplicación era un laborioso proceso basado en sucesivas duplicaciones (la división se basaba en la inversa de este proceso).
Teorema del intercepto de Tales
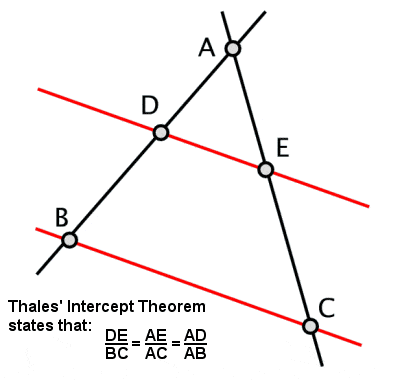
Teorema del intercepto de Tales
Pero la mayor parte de las matemáticas griegas se basaban en la geometría. Se suele considerar que Tales, uno de los Siete Sabios de la Antigua Grecia, que vivió en la costa jónica de Asia Menor en la primera mitad del siglo VI a.C., fue el primero en establecer las pautas para el desarrollo abstracto de la geometría, aunque lo que conocemos de su trabajo (como el de los triángulos semejantes y rectos) parece ahora bastante elemental.
Tales estableció lo que se conoce como el Teorema de Tales, según el cual si un triángulo se dibuja dentro de un círculo con el lado largo como diámetro del círculo, entonces el ángulo opuesto será siempre un ángulo recto (así como algunas otras propiedades relacionadas derivadas de esto). También se le atribuye otro teorema, también conocido como Teorema de Tales o Teorema de la Intercepción, sobre las proporciones de los segmentos de línea que se crean si dos líneas de intersección son interceptadas por un par de paralelas (y, por extensión, las proporciones de los lados de triángulos similares).
Hasta cierto punto, sin embargo, la leyenda del matemático del siglo VI a.C. Pitágoras de Samos se ha convertido en sinónimo del nacimiento de las matemáticas griegas. De hecho, se cree que acuñó las palabras «filosofía» («amor a la sabiduría») y «matemáticas» («lo que se aprende»). Pitágoras fue quizás el primero en darse cuenta de que se podía construir un sistema matemático completo, en el que los elementos geométricos se correspondieran con los números. El teorema de Pitágoras (o teorema de Pitágoras) es uno de los teoremas matemáticos más conocidos. Pero sigue siendo una figura controvertida, como veremos, y las matemáticas griegas no se limitaron en absoluto a un solo hombre.
Tres problemas geométricos
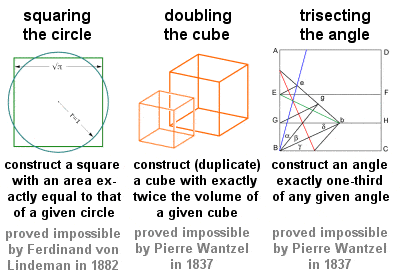
Los Tres Problemas Clásicos
Tres problemas geométricos en particular, a menudo denominados los Tres Problemas Clásicos, y todos ellos a resolver por medios puramente geométricos utilizando sólo una regla y un compás, se remontan a los primeros tiempos de la geometría griega: «la cuadratura del círculo», «la duplicación del cubo» y «la trisección de un ángulo». Estos problemas intransigentes influyeron profundamente en la geometría futura y condujeron a muchos descubrimientos fructíferos, aunque sus soluciones reales (o, como resultó, las pruebas de su imposibilidad) tuvieron que esperar hasta el siglo XIX.
Hipócrates de Quíos (no confundir con el gran médico griego Hipócrates de Kos. Una biografía detallada aquí.) fue uno de esos matemáticos griegos que se aplicó a estos problemas durante el siglo V a.C. (su contribución al problema de la «cuadratura del círculo» se conoce como la Luna de Hipócrates). Su influyente libro «Los Elementos», que data de alrededor del año 440 a.C., fue la primera compilación de los elementos de la geometría, y su obra fue una fuente importante para el trabajo posterior de Euclides.
La Paradoja de Aquiles y la Tortuga de Zenón
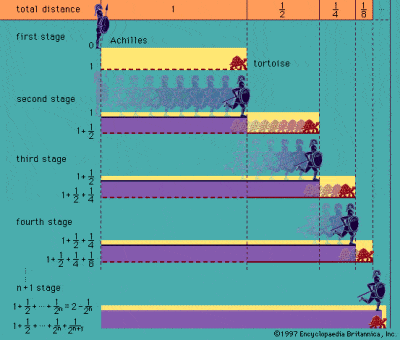
La Paradoja de Aquiles y la Tortuga de Zenón
Fueron los griegos los primeros en enfrentarse a la idea del infinito, tal y como se describe en las conocidas paradojas atribuidas al filósofo Zenón de Elea en el siglo V a.C.. La más famosa de sus paradojas es la de Aquiles y la Tortuga, que describe una carrera teórica entre Aquiles y una tortuga. Aquiles da ventaja a la tortuga, mucho más lenta, pero cuando Aquiles llega al punto de partida de la tortuga, ésta ya se ha adelantado. Para cuando Aquiles llega a ese punto, la tortuga ha vuelto a avanzar, etc, etc, de modo que, en principio, el veloz Aquiles nunca podrá alcanzar a la lenta tortuga.
Paradojas como ésta y la llamada Paradoja de la Dicotomía de Zenón se basan en la infinita divisibilidad del espacio y del tiempo, y se apoyan en la idea de que una mitad más un cuarto más un octavo más un dieciseisavo, etc, etc, hasta el infinito nunca serán iguales a un todo. Sin embargo, la paradoja proviene de la falsa suposición de que es imposible completar un número infinito de rayas discretas en un tiempo finito, aunque es extremadamente difícil demostrar definitivamente la falacia. El antiguo griego Aristóteles fue el primero de muchos en intentar refutar las paradojas, sobre todo porque era un firme creyente de que el infinito sólo podía ser potencial y no real.
Demócrito, más famoso por sus ideas premonitorias acerca de que toda la materia está compuesta por átomos diminutos, fue también un pionero de las matemáticas y la geometría en los siglos V – IV a.C., y produjo obras con títulos como «Sobre los números», «Sobre la geometría», «Sobre las tangencias», «Sobre los mapas» y «Sobre los irracionales», aunque estas obras no han sobrevivido. Sí sabemos que fue uno de los primeros en observar que un cono (o pirámide) tiene un tercio del volumen de un cilindro (o prisma) con la misma base y altura, y es quizás el primero en haber considerado seriamente la división de los objetos en un número infinito de secciones transversales.
Sin embargo, es cierto que Pitágoras, en particular, influyó en gran medida en los que vinieron después de él, incluyendo a Platón, que estableció su famosa Academia en Atenas en el año 387 a.C., y su protegido Aristóteles, cuya obra sobre la lógica se consideró definitiva durante más de dos mil años. El matemático Platón es más conocido por su descripción de los cinco sólidos platónicos, pero no se puede exagerar el valor de su obra como profesor y divulgador de las matemáticas.
Al alumno de Platón, Eudoxo de Cnido, se le suele atribuir la primera aplicación del «método de agotamiento» (desarrollado posteriormente por Arquímedes), un primer método de integración por aproximaciones sucesivas que utilizó para el cálculo del volumen de la pirámide y del cono. También desarrolló una teoría general de la proporción, aplicable tanto a las magnitudes inconmensurables (irracionales) que no pueden expresarse como cociente de dos números enteros, como a las magnitudes conmensurables (racionales), ampliando así las ideas incompletas de Pitágoras.
Sin embargo, la contribución más importante de los griegos -y tanto Pitágoras como Platón y Aristóteles influyeron en este sentido- fue la idea de la demostración, y el método deductivo de utilizar pasos lógicos para demostrar o refutar teoremas a partir de unos axiomas iniciales. Las culturas más antiguas, como la egipcia y la babilónica, se basaban en el razonamiento inductivo, es decir, en el uso de observaciones repetidas para establecer reglas generales. Es este concepto de prueba el que da a las matemáticas su poder y asegura que las teorías probadas sean tan ciertas hoy como lo fueron hace dos mil años, y el que sentó las bases para el enfoque sistemático de las matemáticas de Euclides y los que vinieron después.
| << Volver a las matemáticas egipcias | Adelante con Pitágoras >> |