Los diagramas de bloques consisten en un solo bloque o una combinación de bloques. Se utilizan para representar los sistemas de control en forma pictórica.
Elementos básicos del diagrama de bloques
Los elementos básicos de un diagrama de bloques son un bloque, el punto de suma y el punto de despegue. Consideremos el diagrama de bloques de un sistema de control de lazo cerrado como se muestra en la siguiente figura para identificar estos elementos.
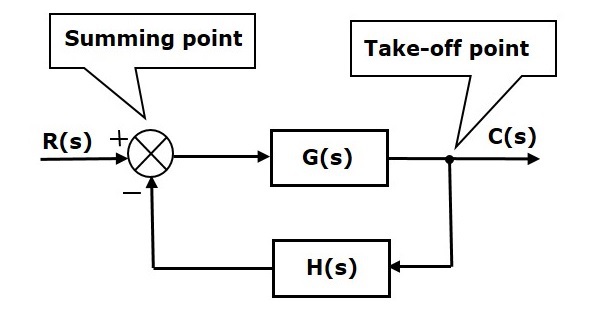
El diagrama de bloques anterior consiste en dos bloques que tienen funciones de transferencia G(s) y H(s). También tiene un punto de suma y un punto de despegue. Las flechas indican la dirección del flujo de señales. Vamos a discutir estos elementos uno por uno.
Bloque
La función de transferencia de un componente está representada por un bloque. El bloque tiene una sola entrada y una sola salida.
La siguiente figura muestra un bloque que tiene la entrada X(s), la salida Y(s) y la función de transferencia G(s).

Función de transferencia,$G(s)={frac{Y(s)}{X(s)}$
$$ flecha derecha Y(s)=G(s)X(s)$$
La salida del bloque se obtiene multiplicando la función de transferencia del bloque por la entrada.
Punto de suma
El punto de suma se representa con un círculo con una cruz (X) en su interior. Tiene dos o más entradas y una sola salida. Produce la suma algebraica de las entradas. También realiza la suma o la resta o la combinación de suma y resta de las entradas en función de la polaridad de las mismas. Veamos estas tres operaciones una por una.
La siguiente figura muestra el punto de suma con dos entradas (A, B) y una salida (Y). Aquí, las entradas A y B tienen signo positivo. Por lo tanto, el punto de suma produce la salida, Y como suma de A y B.
Es decir, Y = A + B.
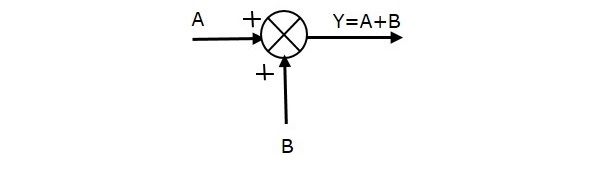
La siguiente figura muestra el punto de suma con dos entradas (A, B) y una salida (Y). Aquí, las entradas A y B tienen signos opuestos, es decir, A tiene signo positivo y B tiene signo negativo. Así, el punto de suma produce la salida Y como la diferencia de A y B.
Y = A + (-B) = A – B.
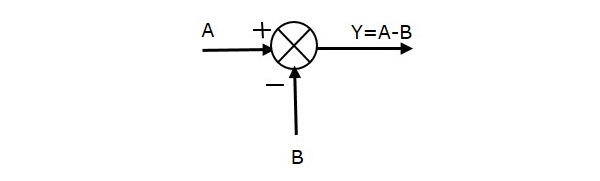
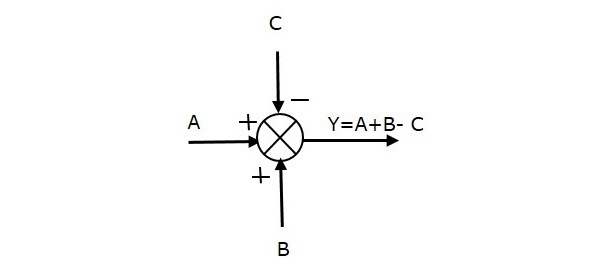
La siguiente figura muestra el punto de suma con tres entradas (A, B, C) y una salida (Y). Aquí, las entradas A y B tienen signo positivo y C tiene signo negativo. Por lo tanto, el punto de suma produce la salida Y como
Y = A + B + (-C) = A + B – C.
Punto de despegue
El punto de despegue es un punto desde el cual la misma señal de entrada puede pasar por más de una rama. Esto significa que con la ayuda del punto de despegue, podemos aplicar la misma entrada a uno o más bloques, sumando puntos.
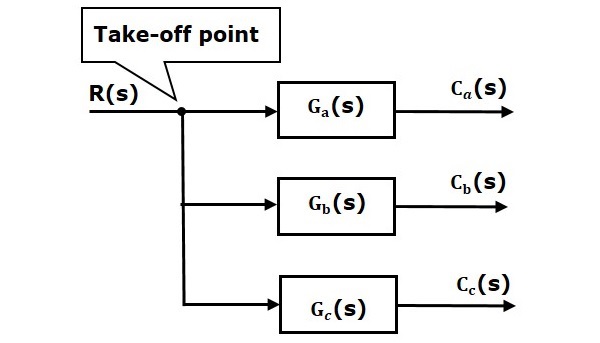
En la siguiente figura, el punto de despegue se utiliza para conectar la misma entrada, R(s) a dos bloques más.
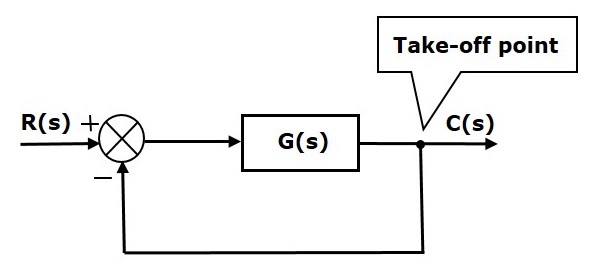
En la siguiente figura, el punto de despegue se utiliza para conectar la salida C(s), como una de las entradas al punto de suma.
Representación en diagrama de bloques de sistemas eléctricos
En esta sección, vamos a representar un sistema eléctrico con un diagrama de bloques. Los sistemas eléctricos contienen principalmente tres elementos básicos – resistencia, inductor y condensador.
Considere una serie de circuito RLC como se muestra en la siguiente figura. Donde, Vi(t) y Vo(t) son las tensiones de entrada y salida. Sea i(t) la corriente que pasa por el circuito. Este circuito está en el dominio del tiempo.
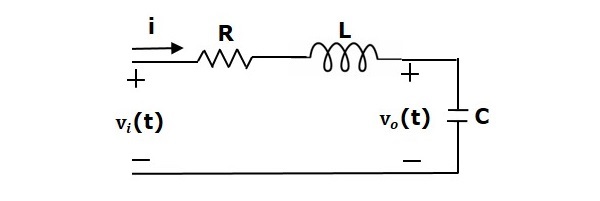
Aplicando la transformada de Laplace a este circuito, se obtendrá el circuito en el dominio s. El circuito es como se muestra en la siguiente figura.
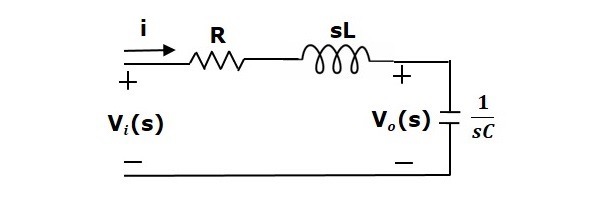
Desde el circuito anterior, podemos escribir
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$$ Flecha derecha I(s)=\frac{1}{R+sL} \V_i(s)-V_o(s) \N-derecha (Ecuación 1)
$V_o(s)=\N-izquierda ( \frac{1}{sC}\N-derecha )I(s)$ (Ecuación 2)
Dibujemos ahora los diagramas de bloques para estas dos ecuaciones individualmente. Y luego combinar esos diagramas de bloques correctamente con el fin de obtener el diagrama de bloques global de la serie de RLC Circuito (s-dominio).
La ecuación 1 se puede implementar con un bloque que tiene la función de transferencia, $\frac{1}{R+sL}$. La entrada y la salida de este bloque son $\left \{ V_i(s)-V_o(s) \right \}$ y $I(s)$. Requerimos un punto de suma para obtener $\left \{ V_i(s)-V_o(s) \right \}$. El diagrama de bloques de la ecuación 1 se muestra en la siguiente figura.
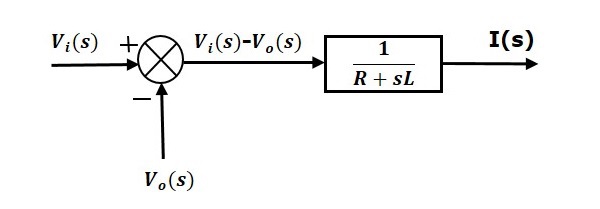
La ecuación 2 se puede implementar con un bloque que tenga función de transferencia, $\frac{1}{sC}$. La entrada y la salida de este bloque son $I(s)$ y $V_o(s)$. El diagrama de bloques de la ecuación 2 se muestra en la siguiente figura.
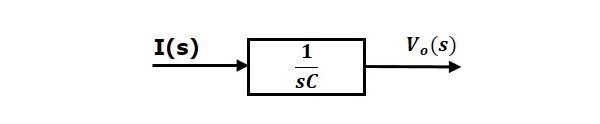
El diagrama de bloques global de la serie del circuito RLC (dominio s) se muestra en la siguiente figura.
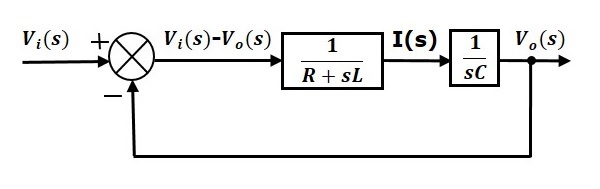
De forma similar, se puede dibujar el diagrama de bloques de cualquier circuito o sistema eléctrico simplemente siguiendo este sencillo procedimiento.
-
Convierta el circuito eléctrico del dominio del tiempo en un circuito eléctrico del dominio s aplicando la transformada de Laplace.
-
Escriba las ecuaciones para la corriente que pasa a través de todos los elementos de la rama en serie y la tensión a través de todas las ramas en derivación.
-
Dibuje los diagramas de bloques para todas las ecuaciones anteriores individualmente.
-
Combine todos estos diagramas de bloques adecuadamente para obtener el diagrama de bloques global del circuito eléctrico (dominio s).