Introduction
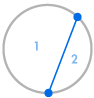
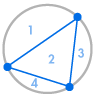
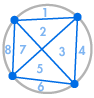
Imaginez que nous plaçons plusieurs points sur la circonférence d’un cercle et que nous relions chaque point entre eux. Cela divise le cercle en de nombreuses régions différentes, et nous pouvons compter le nombre de régions dans chaque cas. Les diagrammes ci-dessous montrent combien de régions il y a pour plusieurs nombres différents de points sur la circonférence. Nous devons nous assurer que seulement deux lignes se rencontrent à chaque intersection à l’intérieur du cercle, et non trois ou plus.
 |
 |
 |
 |
 |
| 1 région | 2 régions | 4 régions | 8 régions | 16 régions |
Nous pouvons immédiatement voir un modèle : le nombre de régions est toujours le double du précédent, de sorte que nous obtenons la séquence 1, 2, 4, 8, 16, … Cela signifie qu’avec 6 points sur la circonférence il y aurait 32 régions, et avec 7 points il y aurait 64 régions.
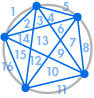
Nous pourrions décider que nous sommes satisfaits de ce résultat. Le nombre de régions est toujours le double du précédent – après tout, cela a fonctionné pour les cinq premiers cas. Ou nous pourrions décider que nous devrions en vérifier quelques autres, juste pour être sûrs :
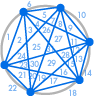 |
 |
| 31 régions, pas 32 | 57 régions, pas 64 |
Malheureusement, quelque chose s’est mal passé : 31 pourrait ressembler à une erreur de comptage, mais 57 est beaucoup moins que 64. La séquence continue 99, 163, 256, …, très différente de ce que nous obtiendrions en doublant le nombre précédent.
Cet exemple illustre pourquoi, en mathématiques, vous ne pouvez pas simplement dire qu’une observation est toujours vraie juste parce qu’elle fonctionne dans quelques cas que vous avez testés. Au lieu de cela, vous devez trouver un argument logique rigoureux qui mène des résultats que vous connaissez déjà, à quelque chose de nouveau dont vous voulez montrer qu’il est vrai. Un tel argument est appelé une preuve.
Les preuves sont ce qui rend les mathématiques différentes de toutes les autres sciences, car une fois que nous avons prouvé quelque chose, nous sommes absolument certains que c’est et sera toujours vrai. Ce n’est pas seulement une théorie qui correspond à nos observations et qui peut être remplacée par une meilleure théorie dans le futur.
Dans l’exemple ci-dessus, nous pourrions compter le nombre d’intersections à l’intérieur du cercle. En réfléchissant bien à la relation entre le nombre d’intersections, de lignes et de régions, nous finirons par trouver une équation différente pour le nombre de régions lorsqu’il y a x = V.Axi points sur le cercle:
Nombre de régions = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Cette équation fonctionne dans tous les cas ci-dessus. Nous pourrions maintenant essayer de la prouver pour chaque valeur de x en utilisant « l’induction », une technique expliquée ci-dessous.
Traditionnellement, la fin d’une preuve est indiquée à l’aide d’un ■ ou □, ou en écrivant QED ou « quod erat demonstrandum », qui est le latin pour « ce qui devait être démontré ».
Un résultat ou une observation que nous pensons être vrai est appelé une Hypothèse ou une Conjecture. Une fois que nous l’avons prouvé, nous l’appelons un Théorème. Une fois que nous avons prouvé un théorème, nous pouvons l’utiliser pour prouver d’autres résultats plus compliqués – construisant ainsi un réseau croissant de théorèmes mathématiques.
Axiomes

L’école d’Athènes de Raphaël : les anciens mathématiciens grecs ont été les premiers à aborder les mathématiques en utilisant un cadre logique et axiomatique.
Une question intéressante est de savoir par où commencer. Comment prouver le premier théorème, si vous ne savez encore rien ? Malheureusement, vous ne pouvez pas prouver quelque chose en utilisant rien. Vous avez besoin d’au moins quelques blocs de construction pour commencer, et ceux-ci sont appelés Axiomes.
Les mathématiciens supposent que les axiomes sont vrais sans pouvoir les prouver. Cependant, ce n’est pas aussi problématique qu’il n’y paraît, car les axiomes sont soit des définitions, soit clairement évidents, et il n’y a que très peu d’axiomes. Par exemple, un axiome pourrait être que a + b = b + a pour deux nombres quelconques a et b.
Les axiomes sont importants à obtenir correctement, car toutes les mathématiques reposent sur eux. S’il y a trop peu d’axiomes, on peut prouver très peu de choses et les mathématiques ne seraient pas très intéressantes. S’il y a trop d’axiomes, on peut prouver presque tout, et les mathématiques ne seraient pas non plus intéressantes. Vous ne pouvez pas non plus avoir des axiomes qui se contredisent.
Les mathématiques ne consistent pas à choisir le bon ensemble d’axiomes, mais à développer un cadre à partir de ces points de départ. Si vous commencez avec des axiomes différents, vous obtiendrez un type de mathématiques différent, mais les arguments logiques seront les mêmes. Chaque domaine des mathématiques a son propre ensemble d’axiomes de base.
Lorsque les mathématiciens ont prouvé un théorème, ils le publient pour que les autres mathématiciens le vérifient. Parfois, ils trouvent une erreur dans l’argument logique, et parfois une erreur n’est trouvée que plusieurs années plus tard. Cependant, en principe, il est toujours possible de décomposer une preuve en axiomes de base.
Théorie des ensembles et axiome du choix

Pour formuler des preuves, il est parfois nécessaire de revenir au fondement même du langage dans lequel les mathématiques sont écrites : la théorie des ensembles.
Un ensemble est une collection d’objets, tels que des nombres. Les éléments d’un ensemble sont généralement écrits entre crochets. Nous pouvons trouver l’union de deux ensembles (l’ensemble des éléments qui sont dans l’un ou l’autre ensemble) ou nous pouvons trouver l’intersection de deux ensembles (l’ensemble des éléments qui sont dans les deux ensembles).
De nombreux problèmes mathématiques peuvent être formulés dans le langage de la théorie des ensembles, et pour les prouver, nous avons besoin des axiomes de la théorie des ensembles. Au fil du temps, les mathématiciens ont utilisé différentes collections d’axiomes, la plus largement acceptée étant neuf axiomes de Zermelo-Fraenkel (ZF):
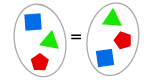
AXIOM DE L’EXTENSION
Si deux ensembles ont les mêmes éléments, alors ils sont égaux.
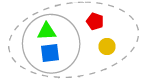
AXIOM DE SÉPARATION
On peut former un sous-ensemble d’un ensemble, qui est constitué de certains éléments.

Axiome d’ensemble incomplet
Il existe un ensemble sans membres, écrit sous la forme {} ou ∅.
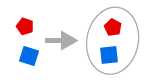
AXIOMME DE L’ENSEMBLE
Donné deux objets x et y on peut former un ensemble {x, y}.
AXIOM DE L’UNION
On peut former l’union de deux ou plusieurs ensembles.
AXIOM DE LA PUISSANCE
Donné un ensemble quelconque, on peut former l’ensemble de tous les sous-ensembles (l’ensemble de la puissance).
AXIOM DE L’INFINITÉ
Il existe un ensemble dont les éléments sont infiniment nombreux.

AXIOM DE FONDATION
Les ensembles sont construits à partir d’ensembles plus simples, ce qui signifie que tout ensemble (non vide) a un membre minimal.
AXIOM DE REMPLACEMENT
Si on applique une fonction à chaque élément d’un ensemble, la réponse est toujours un ensemble.
Si vous pensez à la théorie des ensembles, la plupart de ces axiomes sembleront complètement évidents – et c’est ce que les axiomes sont censés être. Cependant, il y a un dixième axiome qui est plutôt plus problématique :
AXIME DE CHOIX
Donné une infinité d’ensembles non vides, vous pouvez choisir un élément dans chacun de ces ensembles.
À première vue, l’axiome de choix (AC) semble tout aussi innocent que les autres ci-dessus. Cependant l’utilisation de l’infini a un certain nombre de conséquences inattendues. Par exemple, vous pouvez utiliser AC pour prouver qu’il est possible de couper une sphère en cinq morceaux et de les réassembler pour obtenir deux sphères, chacune identique à la sphère initiale. Ce n’est qu’un concept théorique – les coupes requises sont fractales, ce qui signifie qu’elles ne peuvent pas exister dans la vie réelle, et certains des morceaux sont « non mesurables », ce qui signifie qu’ils n’ont pas de volume défini. Mais le fait que l’axiome du choix puisse être utilisé pour construire ces coupes impossibles est assez inquiétant.
Il y a un débat passionné parmi les logiciens, pour savoir s’il faut accepter l’axiome du choix ou non. Chaque collection d’axiomes forme un petit « monde mathématique », et différents théorèmes peuvent être vrais dans différents mondes. Il ne s’agit en fait que de savoir si vous êtes heureux de vivre dans un monde où vous pouvez faire deux sphères à partir d’une seule…
Preuve par Induction
La preuve par Induction est une technique qui peut être utilisée pour prouver qu’un certain énoncé est vrai pour tous les nombres naturels 1, 2, 3, … L' »énoncé » est généralement une équation ou une formule qui inclut une variable n qui pourrait être n’importe quel nombre naturel. Désignons l’énoncé appliqué à n par S(n). Voici les quatre étapes de l’induction mathématique :
- Premièrement, nous prouvons que S(1) est vrai, c’est-à-dire que l’énoncé S est vrai pour 1.
- Nous supposons maintenant que S(k) est vrai, c’est-à-dire que l’énoncé S est vrai pour un certain nombre naturel k.
- En utilisant cette hypothèse, nous essayons de déduire que S(k + 1) est également vrai. Ainsi, chaque fois que S est vrai pour un nombre, il est également vrai pour le nombre suivant.
- Puisque nous savons que S(1) est vrai, S(2) doit être vrai. Et donc S(3) doit être vrai. Et donc S(4) doit être vrai. Et ainsi de suite : S doit être vrai pour tous les nombres.

L’induction peut être comparée à des dominos qui tombent : chaque fois qu’un domino tombe, le suivant tombe aussi. La première étape, qui consiste à prouver que S(1) est vrai, lance la réaction en chaîne infinie.
La première étape est souvent négligée, car elle est si simple. En fait, elle est très importante et toute la chaîne d’induction en dépend – comme le montrent certains des exemples suivants…
Le but du jeu des tours de Hanoi est de déplacer un certain nombre de disques d’un piquet à un autre. Vous n’êtes autorisé à déplacer qu’un seul disque à la fois, et vous n’êtes pas autorisé à mettre un disque plus grand sur un plus petit. Essayez de déplacer la tour de disques du premier piquet au dernier piquet, avec le moins de mouvements possible :
Nombre de disques : Start Over Moves : 0
Une fois que nous avons compris les règles du jeu, nous pouvons essayer de trouver le plus petit nombre d’étapes nécessaires, étant donné un nombre quelconque de disques. Jouer avec le jeu ci-dessus pourrait nous amener à observer que, avec n disques, il faut au moins 2n – 1 étapes. Appelons cette affirmation S(n).
S(1) est clairement vraie puisque, avec un seul disque, on n’a besoin que d’un seul coup, et 21 – 1 = 1.
Passons maintenant pour que S(k) soit vraie, c’est-à-dire qu’il faut 2k – 1 pas pour k disques. Alors si nous avons k + 1 disques :
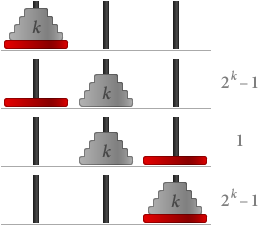
Au total nous avons besoin de (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 étapes. Cela signifie que S(k + 1) est également vrai.
Par induction mathématique, S(n) est vrai pour toutes les valeurs de n, ce qui signifie que la façon la plus efficace de déplacer n = V.Hanoi disques prend 2n – 1 = Math.pow(2,V.Hanoi)-1 coups. ■
Utilisons l’induction pour prouver que la somme des n premiers nombres naturels est n (n + 1)2. Nous vérifions d’abord l’équation pour de petites valeurs de n :
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Puis, nous supposons que le résultat est vrai pour k, c’est-à-dire que 1 + 2 + … + k = k (k + 1)2, où k est un nombre quelconque que nous ne précisons pas. Or
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Nous venons de prouver que si l’équation est vraie pour un certain k, alors elle est aussi vraie pour k + 1. Par induction mathématique, l’équation est vraie pour toutes les valeurs de n. ■
Il existe une autre façon astucieuse de prouver l’équation ci-dessus, qui n’utilise pas l’induction. On prétend que Carl Friedrich Gauss (1777 – 1855), l’un des plus grands mathématiciens de l’histoire, a découvert cette méthode à l’école primaire, lorsque son professeur lui a demandé d’additionner tous les nombres entiers de 1 à 100.
En utilisant l’induction, nous voulons prouver que tous les êtres humains ont la même couleur de cheveux. Soit S(n) l’affirmation que « tout groupe de n êtres humains a la même couleur de cheveux ».
Il est clair que S(1) est vrai : dans tout groupe d’un seul, tout le monde a la même couleur de cheveux.
Posons maintenant S(k), que dans tout groupe de k tout le monde a la même couleur de cheveux. Si nous remplaçons n’importe quel individu du groupe par quelqu’un d’autre, ils forment toujours un total de k et ont donc la même couleur de cheveux. Cela fonctionne pour tout groupe initial de personnes, ce qui signifie que tout groupe de k + 1 a également la même couleur de cheveux. Donc S(k + 1) est vrai.
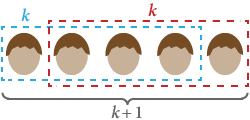
Par induction mathématique, tous les êtres humains ont la même couleur de cheveux ! ■
Il est clair que quelque chose a dû mal tourner dans la preuve ci-dessus – après tout, tout le monde n’a pas la même couleur de cheveux. Pouvez-vous trouver l’erreur ?
Certains théorèmes ne peuvent pas tout à fait être prouvés en utilisant l’induction – nous devons utiliser une version légèrement modifiée appelée Induction forte. Au lieu de supposer S(k) pour prouver S(k + 1), nous supposons tous les S(1), S(2), … S(k) pour prouver S(k + 1). Tout ce qui peut être prouvé en utilisant l’induction (faible) peut clairement aussi être prouvé en utilisant l’induction forte, mais pas vice versa.
Le théorème fondamental de l’arithmétique stipule que tout entier supérieur à 1 est soit un nombre premier, soit il peut être écrit comme le produit de nombres premiers d’une manière essentiellement unique.
Nous pouvons en prouver des parties en utilisant l’induction forte : laissons S(n) être l’énoncé selon lequel « l’entier n est un nombre premier ou peut être écrit comme le produit de nombres premiers ». S(1) est une exception, mais S(2) est clairement vrai car 2 est un nombre premier.
Maintenant, supposons que S(1), S(2), …, S(k) sont tous vrais, pour un certain nombre entier k. Nous savons que k + 1 est soit un nombre premier, soit a des facteurs inférieurs à k + 1. Par hypothèse, nous savons que ces facteurs peuvent être écrits comme le produit de nombres premiers. Par cons× »quent, × moins qu’il ne soit premier, k + 1 peut ךtre × »crit comme un produit de nombres premiers. Cela signifie que S(k + 1) est vrai.
Par induction forte, S(n) est vrai pour tous les nombres n supérieurs à 1. ■
Pour prouver que cette factorisation en nombres premiers est unique (à moins de compter différents ordonnancements des facteurs), il faut plus de travail, mais ce n’est pas particulièrement difficile.
Il s’avère que le principe d’induction faible et le principe d’induction forte sont équivalents : chacun implique l’autre. Ils sont également tous deux équivalents à un troisième théorème, le principe de bon ordonnancement : tout ensemble (non vide) de nombres naturels possède un élément minimal, plus petit que tous les autres.
Le principe de bon ordonnancement est la caractéristique déterminante des nombres naturels. C’est l’un des axiomes de base utilisés pour définir les nombres naturels ![]() = {1, 2, 3, …}. Ces axiomes sont appelés les axiomes de Peano, du nom du mathématicien italien Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …}. Ces axiomes sont appelés les axiomes de Peano, du nom du mathématicien italien Guiseppe Peano (1858 – 1932).
Preuve par contradiction
La preuve par contradiction est une autre technique de preuve importante. Si nous voulons prouver une déclaration S, nous supposons que S n’était pas vrai. En utilisant cette hypothèse, nous essayons de déduire un résultat faux, tel que 0 = 1. Si toutes nos étapes étaient correctes et que le résultat est faux, notre hypothèse initiale devait être fausse. Notre hypothèse initiale était que S n’est pas vrai, ce qui signifie que S est en fait vrai.
Cette technique peut être utilisée dans de nombreuses circonstances différentes, comme prouver que √2 est irrationnel, prouver que les nombres réels sont indénombrables, ou prouver qu’il existe une infinité de nombres premiers.
Voici un autre exemple amusant:
Nous pouvons utiliser la preuve par contradiction, ainsi que le principe de bon ordonnancement, pour prouver que tous les nombres naturels sont « intéressants ».
Supposons que tous les nombres naturels ne sont pas intéressants, et laissons S être l’ensemble des nombres non intéressants. Par le principe du well ordering, S a un plus petit membre x qui est le plus petit nombre non-intéressant. Cette curieuse propriété fait clairement de x un nombre particulièrement intéressant. C’est une contradiction car nous avons supposé que x était non intéressant.
Donc tous les nombres sont intéressants. ■
Gödel et les théorèmes improuvables

Kurt Gödel (1906-1978)
Au début du XXe siècle, les mathématiques ont commencé à se développer rapidement, avec des milliers de mathématiciens travaillant dans d’innombrables nouveaux domaines. David Hilbert (1862 – 1943) a mis en place un vaste programme visant à formaliser les mathématiques et à résoudre toute incohérence dans les fondements des mathématiques. Il s’agissait notamment de prouver tous les théorèmes à l’aide d’un ensemble d’axiomes simples et universels, de prouver que cet ensemble d’axiomes est cohérent et de prouver que cet ensemble d’axiomes est complet, c’est-à-dire que tout énoncé mathématique peut être prouvé ou réfuté à l’aide des axiomes.
Malheureusement, ces plans ont été détruits par Kurt Gödel en 1931. Il a prouvé que dans tout système mathématique (suffisamment complexe) avec un certain ensemble d’axiomes, vous pouvez trouver certaines déclarations qui ne peuvent être ni prouvées ni réfutées en utilisant ces axiomes. Il n’est pas non plus possible de prouver qu’un certain ensemble d’axiomes est cohérent, en n’utilisant rien d’autre que les axiomes eux-mêmes.
La découverte de Gödel est basée sur le fait qu’un ensemble d’axiomes ne peut pas être utilisé pour dire quoi que ce soit sur lui-même, comme par exemple s’il est cohérent. Les problèmes d’autoréférence ne se retrouvent pas seulement en mathématiques mais aussi dans le langage. Voici le paradoxe du menteur :
« Cette phrase est fausse. »
La phrase ci-dessus tente de dire quelque chose sur elle-même. Si elle est vraie, alors la phrase nous dit qu’elle est fausse. Si elle est fausse, alors la phrase nous dit qu’elle n’est pas fausse, c’est-à-dire qu’elle est vraie. En effet, la phrase n’est ni vraie ni fausse.
Lors de leur première publication, les théorèmes de Gödel ont profondément troublé de nombreux mathématiciens. Lorsqu’on entreprend de prouver une observation, on ne sait pas si une preuve existe – le résultat peut être vrai mais indémontrable. Aujourd’hui, nous savons que l’incomplétude est une partie fondamentale non seulement de la logique, mais aussi de l’informatique, qui repose sur des machines effectuant des opérations logiques.
Surprenant, il est possible de prouver que certaines déclarations sont indémontrables. Un exemple est l’hypothèse du continuum, qui concerne la taille des ensembles infinis.
Vers la fin de sa vie, Kurt Gödel a développé de graves problèmes mentaux et il est mort d’auto-affaiblissement en 1978. Ses intuitions sur les fondements de la logique étaient les plus profondes depuis le développement de la preuve par les Grecs anciens.