
Bertrand Russell (1872-1970) et A.N. Whitehead (1861-1947)
Bertrand Russell et Alfred North Whitehead étaient des mathématiciens, logiciens et philosophes britanniques, qui étaient à l’avant-garde de la révolte britannique contre l’idéalisme continental au début du XXe siècle et, à eux deux, ils ont apporté d’importantes contributions dans les domaines de la logique mathématique et de la théorie des ensembles.
Whitehead était l’aîné des deux et venait d’une formation plus pure en mathématiques. Il est devenu le tuteur de Russell au Trinity College de Cambridge dans les années 1890, puis a collaboré avec son ex-élève plus célèbre dans la première décennie du 20e siècle sur leur œuvre monumentale, les « Principia Mathematica ». Toutefois, après la Première Guerre mondiale, que Russell a passée en grande partie en prison en raison de ses activités pacifistes, la collaboration s’est essoufflée et la carrière universitaire de Whitehead est restée à jamais dans l’ombre de celle du plus flamboyant Russell. Il émigra aux États-Unis dans les années 1920, et y passa le reste de sa vie.
Russell est né dans une famille aisée de l’aristocratie britannique, bien que ses parents aient été extrêmement libéraux et radicaux pour l’époque. Ses parents sont morts quand Russell était assez jeune et il a été largement élevé par sa grand-mère farouchement victorienne (bien qu’assez progressiste). Son adolescence a été très solitaire et il a souffert d’épisodes de dépression, affirmant plus tard que seul son amour des mathématiques l’a empêché de se suicider. Il étudie les mathématiques et la philosophie à l’université de Cambridge sous la direction de G.E. Moore et A.N. Whitehead, où il devient un philosophe novateur, un écrivain prolifique sur de nombreux sujets, un athée convaincu, un mathématicien et un logicien inspiré. Aujourd’hui, il est considéré comme l’un des fondateurs de la philosophie analytique, mais il a écrit sur presque tous les grands domaines de la philosophie, en particulier la métaphysique, l’éthique, l’épistémologie, la philosophie des mathématiques et la philosophie du langage.
Russell a été un militant politique engagé et très en vue tout au long de sa longue vie. Il a été un militant anti-guerre de premier plan pendant la Première et la Seconde Guerre mondiale, a défendu le libre-échange et l’anti-impérialisme, et est devenu plus tard un militant strident pour le désarmement nucléaire et le socialisme, et contre Adolf Hitler, le totalitarisme soviétique et l’implication des États-Unis dans la guerre du Vietnam.
Le paradoxe de Russell
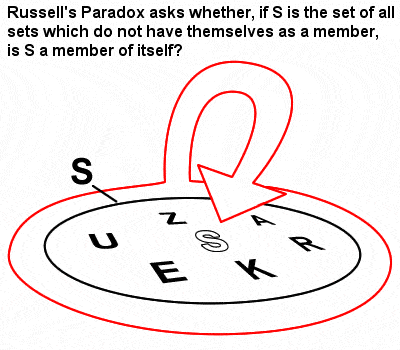
Le paradoxe de Russell
Les mathématiques de Russell ont été grandement influencées par la théorie des ensembles et le logicisme que Gottlob Frege avait développés dans le sillage des premiers travaux révolutionnaires de Cantor sur les ensembles. Dans son « The Principles of Mathematics » de 1903, cependant, il a identifié ce qui est maintenant connu comme le paradoxe de Russell (un ensemble contenant des ensembles qui ne sont pas membres d’eux-mêmes), qui a montré que la théorie naïve des ensembles de Frege pouvait en fait conduire à des contradictions.
Le paradoxe est parfois illustré par cet exemple simpliste : « Si un barbier rase tous et seulement les hommes du village qui ne se rasent pas eux-mêmes, se rase-t-il lui-même ? »
Le paradoxe semblait impliquer que l’on ne pouvait plus faire confiance aux fondements mêmes de l’ensemble des mathématiques, et que, même en mathématiques, la vérité ne pourrait jamais être connue de manière absolue (les travaux ultérieurs de Gödel et de Turing ne feraient qu’aggraver la situation). La critique de Russell était suffisante pour ébranler la confiance de Frege dans l’ensemble de l’édifice du logicisme, et il était assez gracieux pour l’admettre ouvertement dans un appendice écrit à la hâte au volume II de ses « Lois fondamentales de l’arithmétique ».
Mais l’opus magnum de Russell était le monolithique « Principia Mathematica », publié en trois volumes en 1910, 1912 et 1913. Le premier volume a été co-écrit par Whitehead, bien que les deux derniers soient presque entièrement l’œuvre de Russell. L’aspiration de cette œuvre ambitieuse n’était rien de moins qu’une tentative de dériver toutes les mathématiques à partir d’axiomes purement logiques, tout en évitant les types de paradoxes et de contradictions trouvés dans les travaux antérieurs de Frege sur la théorie des ensembles. Russell y est parvenu en utilisant une théorie ou un système de « types », dans lequel chaque entité mathématique est affectée à un type au sein d’une hiérarchie de types, de sorte que les objets d’un type donné sont construits exclusivement à partir d’objets de types précédents situés plus bas dans la hiérarchie, ce qui évite les boucles. Chaque ensemble d’éléments, alors, est d’un type différent de chacun de ses éléments, de sorte que l’on ne peut pas parler de « l’ensemble de tous les ensembles » et de constructions similaires, qui conduisent à des paradoxes.
Cependant, les « Principia » exigeaient, en plus des axiomes de base de la théorie des types, trois autres axiomes qui semblaient ne pas être vrais en tant que simples questions de logique, à savoir l' »axiome de l’infini » (qui garantit l’existence d’au moins un ensemble infini, à savoir l’ensemble de tous les nombres naturels), l' »axiome du choix » (qui garantit que, étant donné toute collection de « bacs », contenant chacun au moins un objet, il est possible de faire une sélection d’exactement un objet dans chaque bac, même s’il y a une infinité de bacs, et qu’il n’y a pas de « règle » pour savoir quel objet choisir dans chacun) et l' »axiome de réductibilité » propre à Russell (qui stipule que toute fonction de vérité propositionnelle peut être exprimée par une fonction de vérité prédicative formellement équivalente).
Pendant les quelque dix années que Russell et Whitehead ont consacrées aux « Principia », brouillon après brouillon a été commencé et abandonné, Russell repensant constamment ses prémisses de base. Russell et sa femme Alys ont même emménagé chez les Whitehead afin d’accélérer le travail, bien que son propre mariage ait souffert de l’engouement de Russell pour la jeune épouse de Whitehead, Evelyn. Finalement, Whitehead insista sur la publication de l’œuvre, même si elle n’était pas (et pourrait ne jamais être) complète, bien qu’ils aient été contraints de la publier à leurs propres frais car aucun éditeur commercial ne voulait y toucher.
Principia Mathematica

Une petite partie de la longue preuve que 1+1 =2 dans les « Principia Mathematica »
On peut se faire une idée de la portée et de l’exhaustivité des « Principia » en constatant qu’il faut plus de 360 pages pour prouver définitivement que 1 + 1 = 2.
Aujourd’hui, il est largement considéré comme l’une des œuvres les plus importantes et séminales en logique depuis l' »Organon » d’Aristote. Il semblait remarquablement réussi et résistant dans ses objectifs ambitieux, et a rapidement acquis une renommée mondiale pour Russell et Whitehead. En effet, ce n’est que le théorème d’incomplétude de Gödel en 1931 qui a finalement montré que les « Principia » ne pouvaient pas être à la fois cohérents et complets.
Russell a reçu l’Ordre du mérite en 1949 et le prix Nobel de littérature l’année suivante. Sa renommée ne cessa de croître, même en dehors des cercles académiques, et il devint une sorte de nom familier à la fin de sa vie, bien qu’en grande partie à cause de ses contributions philosophiques et de son activisme politique et social, qu’il poursuivit jusqu’à la fin de sa longue vie. Il est mort de la grippe dans son pays de Galles bien-aimé à l’âge de 97 ans.
| << Retour à Hardy et Ramanujan | En avant vers Hilbert >> |
.