Qu’est-ce qu’un réseau ?
Un réseau est un tableau ordonné de points décrivant l’arrangement des particules qui forment un cristal.
La cellule unitaire d’un cristal est définie par les points du réseau.La cellule unitaire est la plus petite partie d’un cristal qui, répétée régulièrement par translation en trois dimensions, crée le cristal entier.
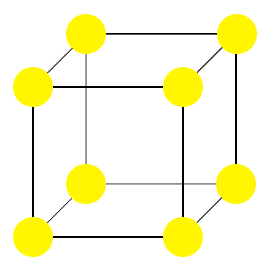
Par exemple, l’image montrée ici est la cellule unitaire d’une structure cubique primitive.
Dans la structure dessinée, toutes les particules (jaunes) sont les mêmes.Dans ce cas particulier, les points du réseau définissant la cellule unitaire coïncident avec les centres des particules du cristal. Ce n’est pas forcément toujours le cas.
Le réseau ionique
Si un cristal est formé d’ions, le composé peut être décrit comme un réseau ionique.
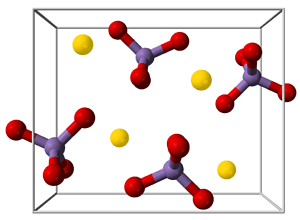
Des exemples bien connus de treillis ioniques sont le chlorure de sodium, le permanganate de potassium, le borax (borate de sodium) et le sulfate de cuivre(II).

Le réseau covalent
Si un cristal est constitué d’atomes liés de manière covalente, il peut être décrit comme un réseau covalent ou un réseau covalent infini.
Les exemples bien connus de réseaux covalents sont le diamant, le quartz (dioxyde de silicium), le silicium et l’étain gris.
Constantes du réseau
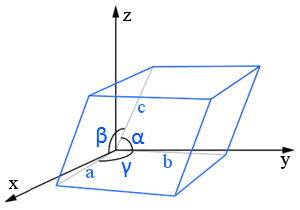
Les constantes du réseau (ou paramètres du réseau) sont les longueurs et les angles entre des bords de la cellule unitaire.
Dans ce diagramme de treillis parallélépipédique, les constantes du treillis sont a, b, et c (longueurs) et α, β, et γ (angles).
Structures de treillis
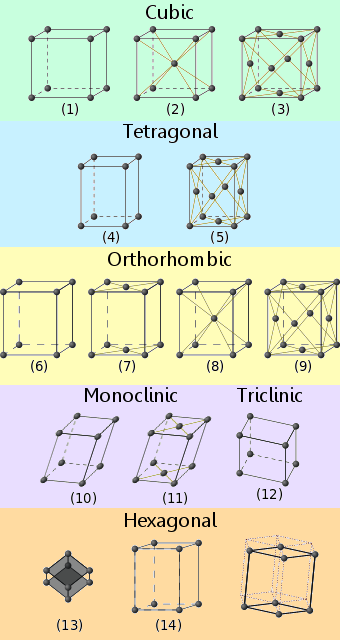
Les matériaux cristallins s’inscrivent dans l’un des quatorze arrangements de réseau reconnus.Ils sont connus sous le nom de réseaux de Bravais.
Les noms des systèmes de réseaux cristallins, correspondant aux numéros sur les diagrammes, sont les suivants :
1. Cubique primitif
2. Cubique centré sur le corps
3. Cubique centré sur la face
4. Tétragonal primitif
5. Tétragonal centré sur le corps
6. orthorhombique primitif
7. orthorhombique centré sur la base
8. Orthorhombique centré sur le corps
9. Orthorhombique centré sur la face
10. Monoclinique primitif
11. Monoclinique centré sur la base
12. Triclinique
13. Rhomboédrique
14. Hexagonale
Défauts de réseau
Si l’on supposait qu’un cristal est basé sur un réseau ionique mathématiquement parfait, sa résistance à la traction calculée serait beaucoup plus grande que ce qui est réellement observé.