Disséquer la masse du proton

APS/Alan Stonebraker

APS/Alan Stonebraker

×

Presque toute la masse de la matière connue est contenue dans les protons et les neutrons – les particules qui composent les noyaux des atomes. Mais comment les protons et les neutrons acquièrent-ils leur masse ? Chacune de ces particules, ou « nucléons », est composée d’un amas dense et mousseux d’autres particules : les quarks, qui ont une masse, et les gluons, qui n’en ont pas. Pourtant, la masse des quarks ne représente que 1 % de la masse d’un proton ou d’un neutron, l’essentiel de la masse du proton provenant uniquement du mouvement et du confinement des quarks et des gluons. Yi-Bo Yang, de la Michigan State University, à East Lansing, et ses collègues ont quantifié, pour la première fois, quatre contributions distinctes à la masse du proton grâce à un calcul basé sur la chromodynamique quantique (CDQ), la théorie fondamentale de l’interaction forte dans le noyau et une pierre angulaire du modèle standard de la physique des particules. Alors que cette décomposition en quatre parties est connue depuis plus de 20 ans , la compréhension qu’en ont les physiciens n’a été que qualitative.

Les quarks qui composent le proton et le neutron sont des particules fondamentales, qui obtiennent leur masse grâce au mécanisme de Higgs. Ce même mécanisme n’explique pas la masse du proton, qui est composé de deux quarks up ( 2,4MeV∕c2 chacun) et d’un quark down ( 5,0MeV∕c2) . Il est clair que la somme de ces trois masses est loin de correspondre à la masse réelle du proton, soit 938,27MeV∕c2. La mécanique quantique nous apprend qu’il existe également une masse (ou une énergie équivalente) associée au confinement des quarks dans le proton, dont le diamètre est d’environ 10-15 m. En utilisant un argument de principe d’incertitude, la position confinée des particules se traduit par un grand momentum et devrait ajouter environ 300MeV∕c2-dans le bon ball park de la masse du proton, mais encore trop faible. (Des arguments similaires s’appliquent au neutron, qui est composé de deux quarks down et d’un quark up.)

En fait, des prédictions précises du modèle standard de la masse du proton et du neutron existent depuis une décennie . Aux faibles énergies pertinentes pour un noyau, ces masses peuvent être prédites à partir de seulement trois paramètres : une échelle de masse globale, qui est générée dynamiquement dans la CDQ, et les paramètres des quarks up et down. Les masses du proton et du neutron sont connues avec beaucoup plus de précision grâce à l’expérience que ne le permettront jamais les prédictions du modèle standard. Cependant, les physiciens aimeraient comprendre comment les masses émergent de la CDQ, de la même manière qu’ils peuvent prédire le spectre de l’hydrogène à partir de la théorie quantique.

Yang et ses collègues l’ont fait, en déterminant pour la première fois les différentes contributions à la masse du proton qui proviennent de la dynamique des quark et des gluons . Les chercheurs s’appuient sur une méthode puissante connue sous le nom de QCD en treillis, qui place les quarks sur les sites d’un treillis et les gluons sur les liens entre eux. Cette représentation rigoureuse de la CDQ peut être implémentée numériquement, et c’est la seule méthode basée sur la CDQ qui peut faire des prédictions quantitatives sur des échelles de longueur comparables à celle du proton ou plus grandes. (À ces échelles, les interactions entre les quarks et les gluons sont si fortes qu’elles ne peuvent pas être traitées avec les diagrammes de Feynman et autres méthodes « perturbatives »). Cependant, la CDQ sur treillis est une technique coûteuse. La discrétisation crée des erreurs, et pour les éliminer, il faut ramener l’espacement du réseau, a, à zéro. Dans la pratique, cette étape est réalisée en effectuant de multiples calculs à différentes valeurs de a, ce qui entraîne un coût numérique élevé qui s’échelonne comme a-6. Néanmoins, la CDQ sur treillis a considérablement évolué ces dernières années, permettant la détermination la plus précise des masses des quark et de nombreuses propriétés des mésons légers et lourds , qui sont composés d’un quark et d’un antiquark.

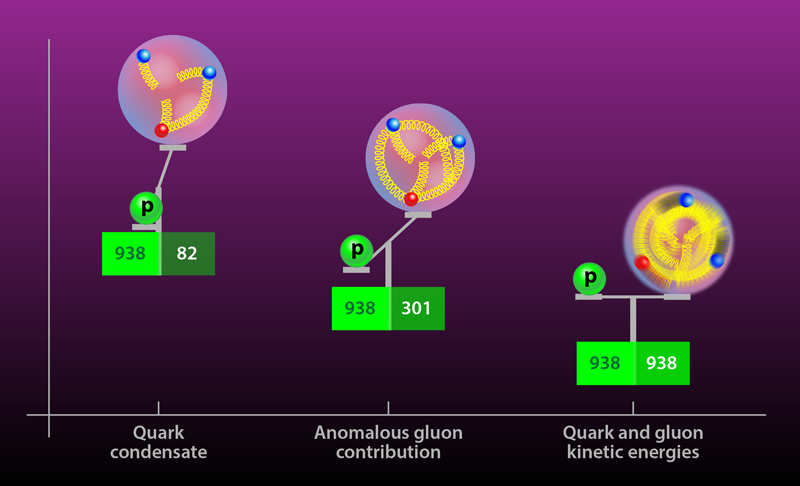
Une particule à trois quark comme le nucléon est exponentiellement plus compliquée pour la CDQ sur treillis, et les calculs réussis, avec toutes les sources d’incertitude contrôlées, ont été rares. Dans leurs travaux, Yang et ses collaborateurs ont surmonté certaines de ces complications en utilisant de nouvelles méthodes de calcul qu’ils ont, avec d’autres, développées . Ces avancées leur ont permis de calculer la contribution à la masse du proton provenant de quatre sources connues sous le nom de condensat de quark ( ∼9 %), d’énergie de quark ( ∼32 %), d’énergie de champ gluonique ( ∼37 %) et de contribution gluonique anormale ( ∼23 %) (figure 1). La plus petite contribution, le condensat de quark, est un mélange des quarks up et down et d’une  » mer  » de quarks étranges virtuels, et c’est la seule qui disparaîtrait si les masses des quark étaient nulles. Les trois autres termes sont tous liés à la dynamique des quarks et des gluons et à leur confinement dans le proton. L’énergie des quarks et l’intensité du champ gluonique correspondent à l’énergie cinétique des quarks confinés et des gluons confinés, respectivement. Le terme anomal est un effet purement quantique. Il est associé à l’échelle de masse de la CDQ et consiste en des contributions de condensats de toutes les saveurs de quarks, y compris les quarks étranges, charmants, inférieurs et supérieurs. Les calculs de Yang et de ses collègues montrent que, si les masses des quarks supérieur, inférieur et étrange étaient toutes nulles, le proton aurait encore plus de 90 % de sa masse expérimentale. En d’autres termes, presque toute la masse connue de l’Univers provient de la dynamique des quarks et des gluons.

Les physiciens souhaitent depuis longtemps comprendre l’émergence de la masse du nucléon en termes de modèle standard, et les résultats de Yang et de ses collègues constituent une contribution importante à cet objectif. Leur travail et d’autres travaux similaires marquent également le début d’une nouvelle ère, dans laquelle notre compréhension des nucléons est de plus en plus façonnée par des prédictions quantitatives basées sur la QCD en treillis. Cette année encore, des chercheurs ont utilisé la CDQ en treillis pour déterminer la charge axiale des nucléons, une quantité omniprésente en physique nucléaire, avec une précision sans précédent de 1 %. La CDQ en treillis, associée à de puissantes méthodes analytiques permettant de simplifier les calculs de CDQ, permettra de mieux comprendre la sous-structure du nucléon, qui est étudiée dans divers collisionneurs à travers le monde et qui serait l’un des points forts d’une machine proposée appelée collisionneur électron-ion. En fin de compte, l’espoir est que la CDQ en treillis puisse être appliquée à un noyau (plusieurs nucléons). Les noyaux sont utilisés comme détecteurs dans plusieurs expériences de recherche de physique au-delà du modèle standard, comme la matière noire, un moment dipolaire électrique permanent et la désintégration double bêta sans neutrinol. L’interprétation de ces expériences nécessitera une compréhension quantitative de la physique nucléaire ancrée dans le modèle standard. Ce genre de problème complexe est de plus en plus dans le domaine de la QCD en treillis grâce à la disponibilité des ordinateurs quasi exascale, Sierra et Summit, qui sont mis en ligne maintenant et sont 10 à 15 fois plus puissants que même ceux utilisés par Yang et ses collègues.

Cette recherche est publiée dans Physical Review Letters.

1. Y.-B.. Yang, J. Liang, Y.-J. Bi, Y. Chen, T. Draper, K.-F. Liu, et Z. Liu,  » Proton mass decomposition from the QCD energy momentum tensor « , Phys. Rev. Lett. 121, 212001 (2018).
2. X.-D. Ji, « QCD analysis of the mass structure of the nucleon », Phys. Rev. Lett. 74, 1071 (1995).
3. S. Aoki et al, « Review of lattice results concerning low-energy particle physics, » Eur. Phys. J. C 77, 112 (2017) ; Les quarks n’ont pas de masse au sens où l’électron en a une. Mais un paramètre de masse pour les quarks peut toujours être défini de manière rigoureuse avec un schéma de renormalisation et une échelle spécifiés. Les masses citées par Aoki et al. sont dans le schéma dit MS-bar à une échelle de 2 GeV.
4. S. Durr et al. « Ab initio determination of light hadron masses », Science 322, 1224 (2008).
5. A. Bazavov et al. « Up-, down-, strange-, charm-, and bottom-quark masses from four-flavor lattice QCD, » Phys. Rev. D 98, 054517 (2018).
6. K-F. Liu, J. Liang, et Y.-B, Yang, « Réduction de la variance et décomposition en grappes », Phys. Rev. D 97, 034507 (2018).
7. Y.-B. Yang, M. Gong, J. Liang, H.-W. Lin, K.-F. Liu, D. Pefkou et P. Shanahan, « Nonperturbatively renormalized glue momentum fraction at the physical pion mass from lattice QCD, » Phys. Rev. D 98, 074506 (2018).
8. Y.-B.. Yang, R. Sufian, A. Alexandru, T. Draper, M.J. Glatzmaier, K.-F. Liu, et Y. Zhao,  » Glue spin and helicity in the proton from lattice QCD « , Phys. Rev. Lett. 118, 102001 (2017).
9. C. C. Chang et al. « A per-cent-level determination of the nucleon axial coupling from quantum chromodynamics », Nature 558, 91 (2018).
10. H.-W. Lin et al, « Parton distributions and lattice QCD calculations : Un livre blanc de la communauté « , Prog. Part. Nucl. Phys. 100, 107 (2018).

A propos de l’auteur

André Walker-Loud est un scientifique du personnel au Lawrence Berkeley National Laboratory (LBNL). Il a obtenu son doctorat à l’Université de Washington, à Seattle. Il a ensuite occupé des postes de recherche postdoctorale à l’Université du Maryland, au College of William & Mary (W&M) et au LBNL, puis a été nommé conjointement professeur adjoint de physique à W&M et scientifique principal au Thomas Jefferson National Accelerator Facility. Dans ses recherches, il utilise la QCD en treillis et la théorie des champs effectifs pour acquérir une compréhension quantitative de la manière dont la physique nucléaire émerge de la QCD. Il s’intéresse également à sonder les limites du modèle standard en testant les symétries fondamentales dans des environnements nucléaires.

Domaines d’activité

Plus d’articles