La méthode Delta-Delta Ct ou méthode Livak est la méthode la plus privilégiée pour l’analyse des données de qPCR. Cependant, elle ne peut être utilisée que lorsque certains critères sont remplis.Veuillez vous référer aux notes de cours pour vous assurer que ces critères sont remplis. Si ce n’est pas le cas, une méthode plus généralisée est appelée méthode de Pfaffl. Veuillez lire le matériel de lecture supplémentaire pour obtenir plus d’informations sur cette méthode.
Voici les étapes pour la méthode de Livak:
Le fichier Excel avec tous les calculs sont dans le dossier d’analyse qPCR sur Blackboard.
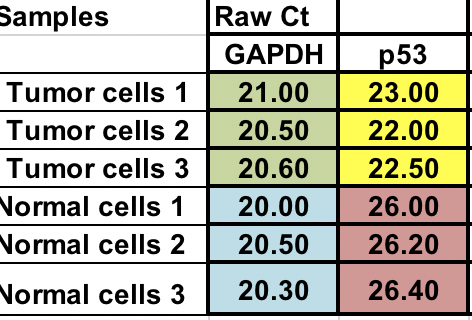
Vous avez le Ct brut (nombre de cycles qu’il faut pour atteindre le seuil) pour les cellules normales et tumorales (3 répliques pour chacune).
Normalisation¶
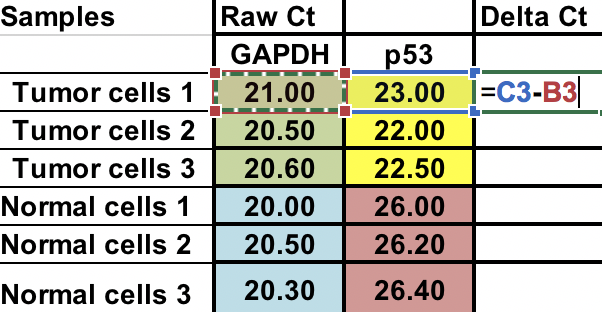
D’abord, vous devrez calculer la différence relative entre le gène d’intérêt (p53) et le gène domestique (GAPDH).
∆Ct = Ct (gène d’intérêt) – Ct (gène domestique)
Moyenne des échantillons de contrôle (cellules normales)¶
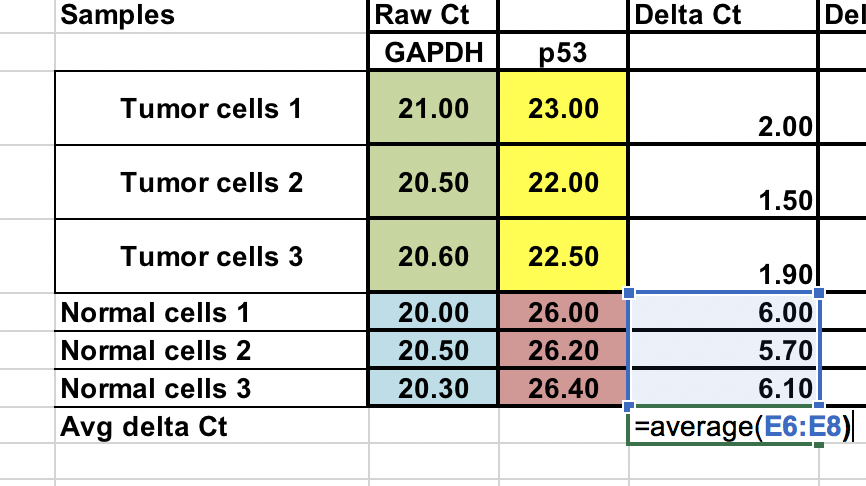
Comme nous comparons notre tumeur (traitement) au contrôle (cellules normales), nous devons d’abord faire la moyenne des ∆Ct des 3 échantillons de contrôle (normaux).
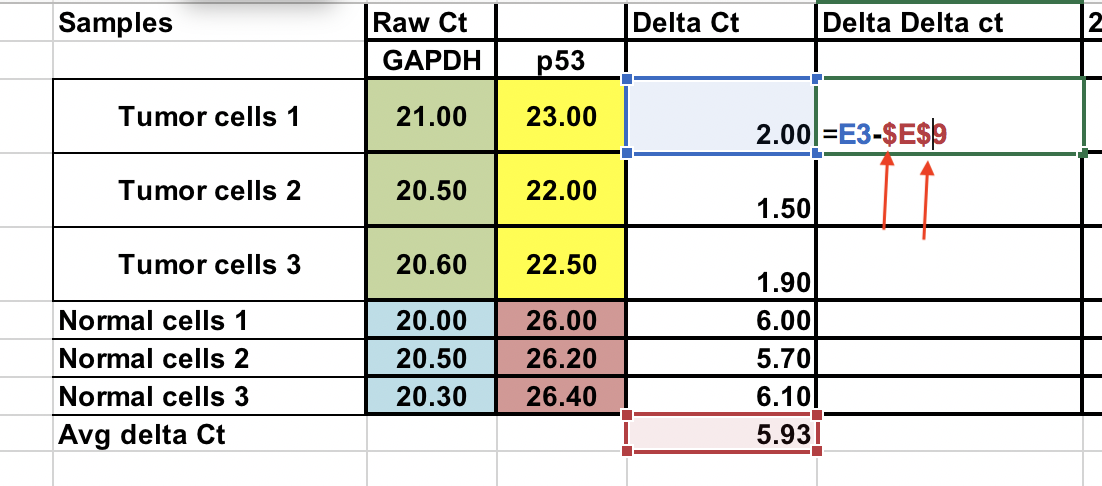
Calculer le ∆∆Ct par rapport à la moyenne des ∆Ct. cells¶
∆∆Ct = ∆Ct (échantillon de tumeur) – ∆Ct (moyenne normale)
Vous pouvez faire cela des échantillons normaux également. Utilisez les signes $ devant le numéro de colonne et la lettre brute (flèches) pour fixer la cellule.
Expression génique pliée pour chaque échantillon¶
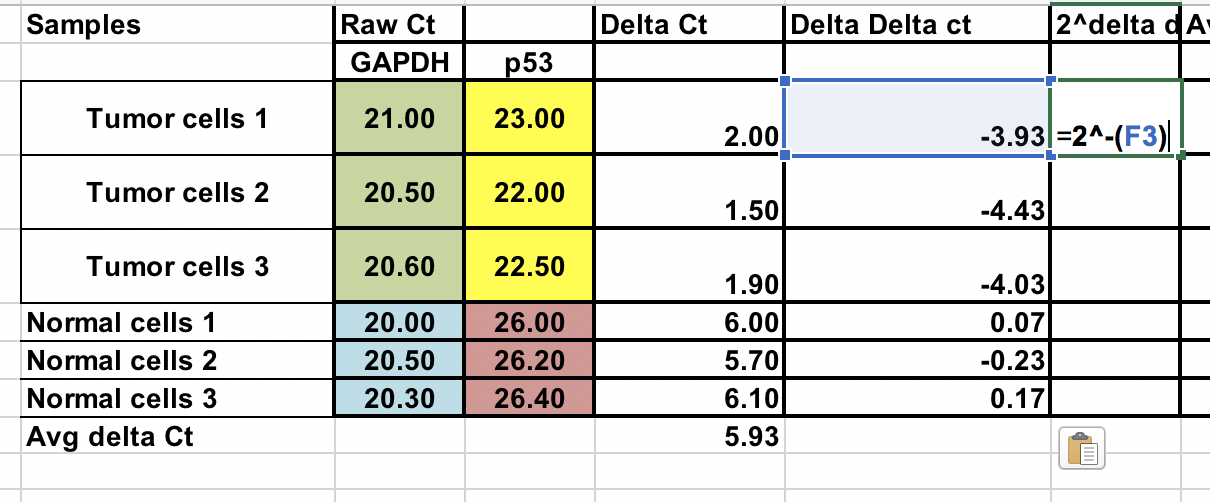
Assurez-vous d’élever le ∆∆Ct négatif à la puissance deux.
Expression génique pliée = 2^-(∆∆Ct)
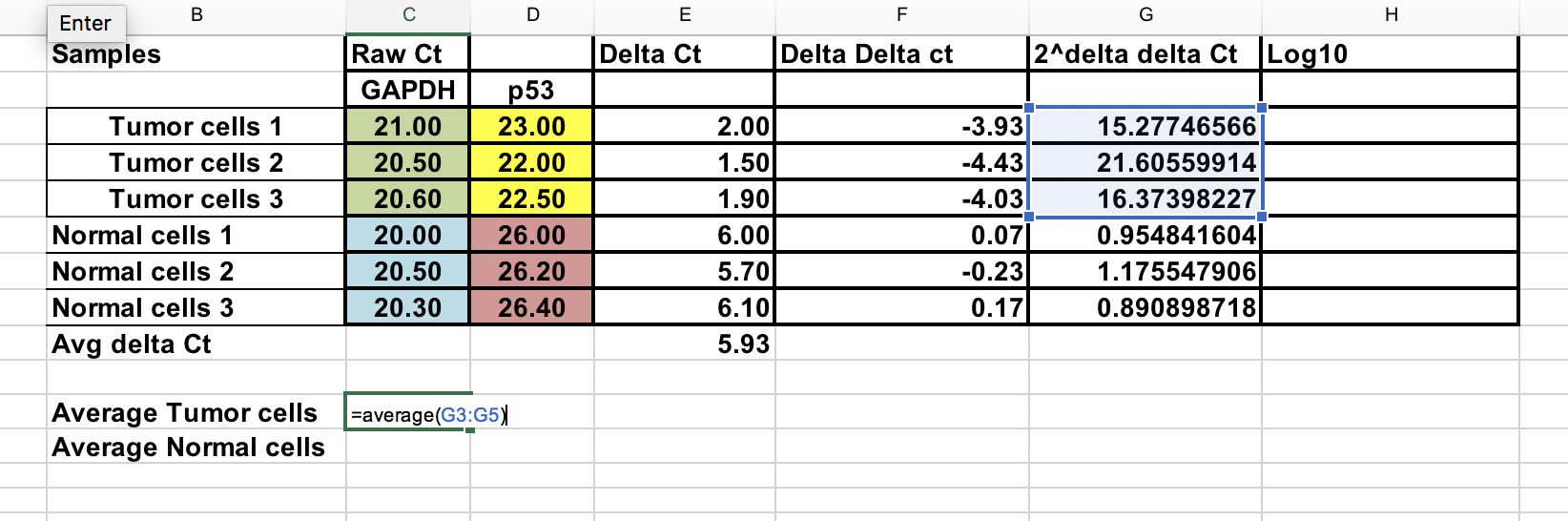
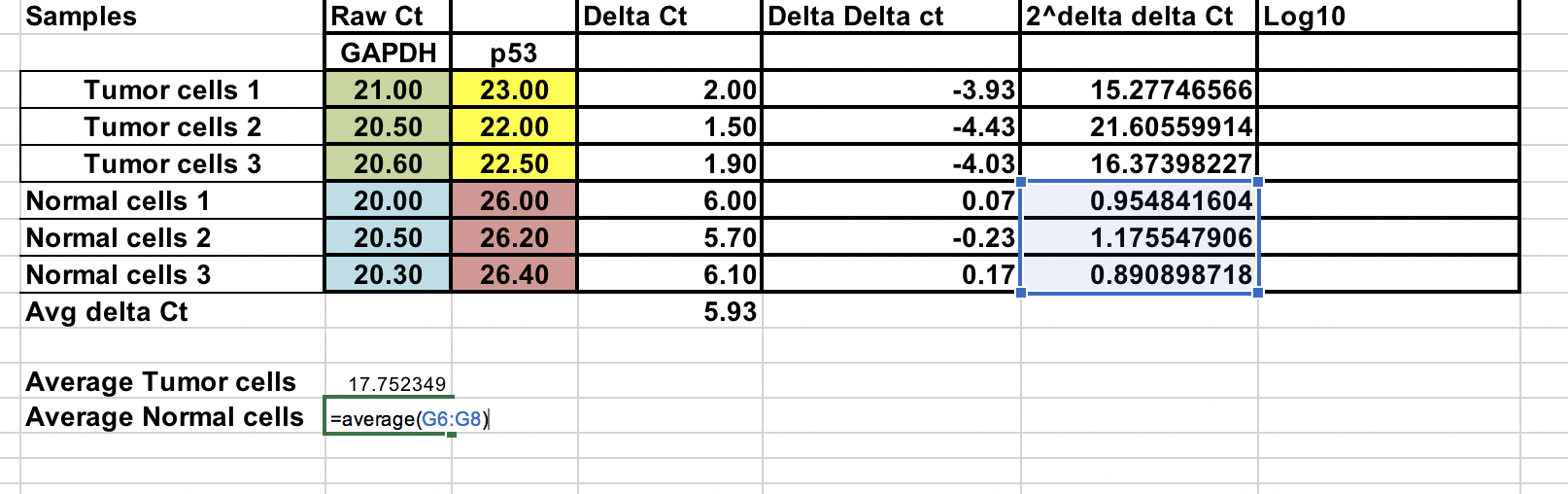
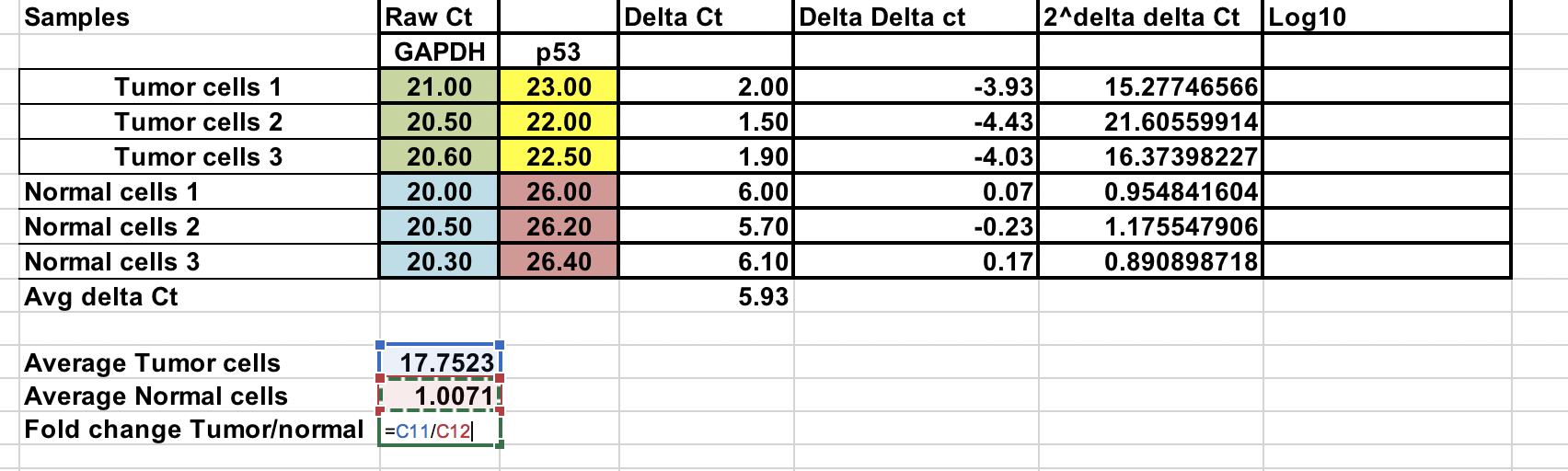
Changement de pli global¶
Vous pouvez calculer le changement de pli moyen pour les échantillons tumoraux et normaux. Rapport entre ces deux le changement de pli entre la tumeur et les échantillons normaux.
Transformation logarithmique¶
Pour effectuer des tests statistiques paramétriques tels que le test T, il est conseillé de transformer les résultats finaux d’expression génique en valeurs logarithmiques (toute base logarithmique). Cela rendrait la distribution des données symétrique.
Ici nous avons changé le 2^-(∆∆Ct) en log 10.
T-test¶
Il faut être prudent lors de l’utilisation de tests paramétriques si les données ne sont pas normalement distribuées, cela conduirait à des conclusions erronées.
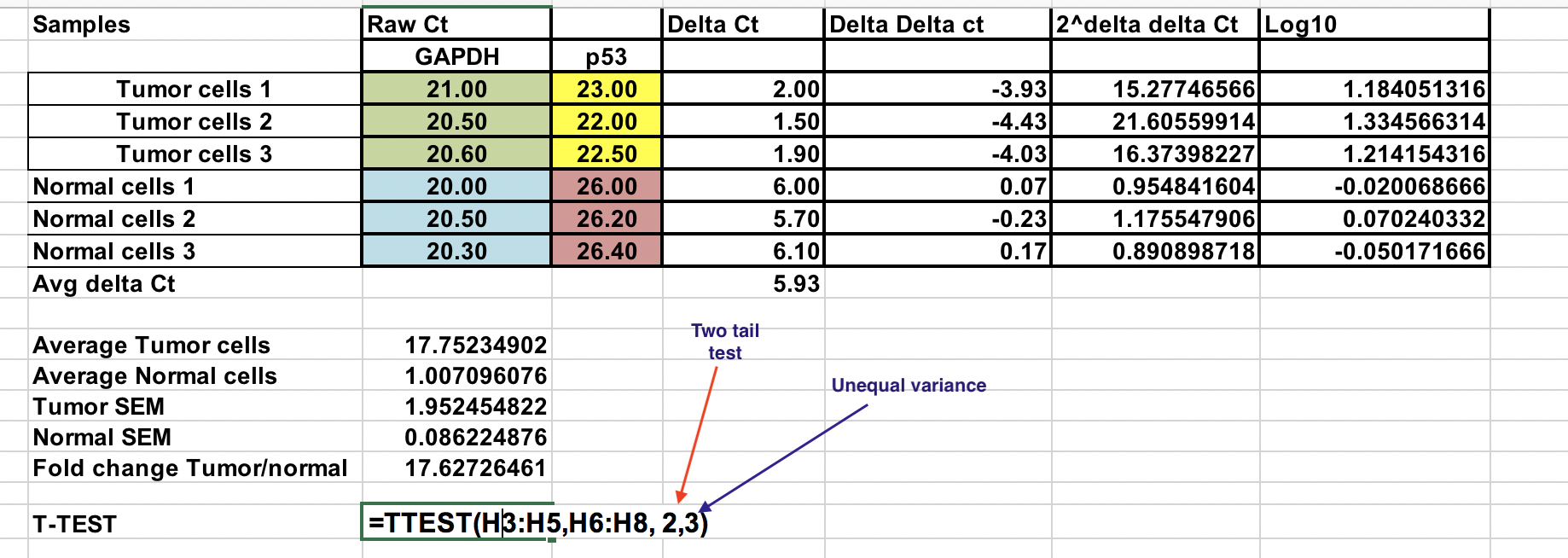
Sélectionner le log 10 des valeurs 2^-(∆∆Ct) pour les échantillons normaux et tumoraux comme indiqué. Utiliser le test à deux queues (numéro 2) et supposer une variance inégale (3).
La valeur P résultante est inférieure à 0,05 et donc, nous rejetons l’hypothèse nulle et les moyennes de deux échantillons sont significativement différentes au niveau de 0,05.
.