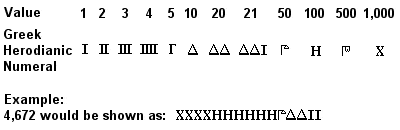
Numérotation grecque ancienne hérodienne
Alors que l’empire grec commençait à étendre sa sphère d’influence en Asie Mineure, Mésopotamie et au-delà, les Grecs ont été assez intelligents pour adopter et adapter des éléments utiles des sociétés qu’ils ont conquises. C’était aussi vrai pour les mathématiques que pour toute autre chose, et ils ont adopté des éléments de mathématiques des Babyloniens et des Égyptiens. Mais ils n’ont pas tardé à apporter des contributions importantes de leur propre chef et, pour la première fois, nous pouvons reconnaître les contributions individuelles. À l’époque hellénistique, les Grecs avaient présidé à l’une des révolutions les plus spectaculaires et les plus importantes de la pensée mathématique de tous les temps.
Numérotation attique ou hérodienne
Le système numéral grec ancien, connu sous le nom de numérotation attique ou hérodienne, était entièrement développé vers 450 avant notre ère, et en usage régulier peut-être dès le 7e siècle avant notre ère. Il s’agissait d’un système en base 10 similaire au système égyptien antérieur (et encore plus similaire au système romain ultérieur), avec des symboles pour 1, 5, 10, 50, 100, 500 et 1 000 répétés autant de fois que nécessaire pour représenter le nombre souhaité. L’addition se faisait en totalisant séparément les symboles (1, 10, 100, etc) des nombres à ajouter, et la multiplication était un processus laborieux basé sur des doublons successifs (la division était basée sur l’inverse de ce processus).
Théorème de l’interception de Thalès
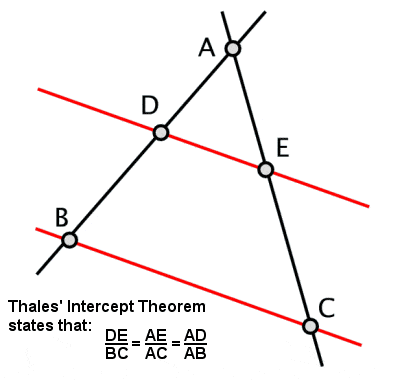
Théorème de l’interception de Thalès
Mais la plupart des mathématiques grecques étaient basées sur la géométrie. Thalès, l’un des sept sages de la Grèce antique, qui vivait sur la côte ionienne de l’Asie mineure dans la première moitié du VIe siècle avant notre ère, est généralement considéré comme ayant été le premier à établir des lignes directrices pour le développement abstrait de la géométrie, bien que ce que nous savons de son travail (comme sur les triangles semblables et droits) semble aujourd’hui assez élémentaire.
Thalès a établi ce qui est devenu connu sous le nom de théorème de Thalès, selon lequel si un triangle est dessiné dans un cercle dont le grand côté est un diamètre du cercle, alors l’angle opposé sera toujours un angle droit (ainsi que quelques autres propriétés connexes dérivées de cela). On lui attribue également un autre théorème, également connu sous le nom de théorème de Thalès ou de théorème de l’interception, concernant les rapports des segments de droite qui sont créés si deux lignes sécantes sont interceptées par une paire de parallèles (et, par extension, les rapports des côtés de triangles similaires).
Dans une certaine mesure, cependant, la légende du mathématicien Pythagore de Samos, du 6e siècle avant notre ère, est devenue synonyme de la naissance des mathématiques grecques. En effet, on pense qu’il a inventé les mots « philosophie » (« amour de la sagesse ») et « mathématiques » (« ce qui est appris »). Pythagore a peut-être été le premier à réaliser qu’il était possible de construire un système mathématique complet, dans lequel les éléments géométriques correspondent à des nombres. Le théorème de Pythagore (ou théorème de Pythagore) est l’un des plus connus de tous les théorèmes mathématiques. Mais il reste un personnage controversé, comme nous le verrons, et les mathématiques grecques ne se limitaient en aucun cas à un seul homme.
Trois problèmes géométriques
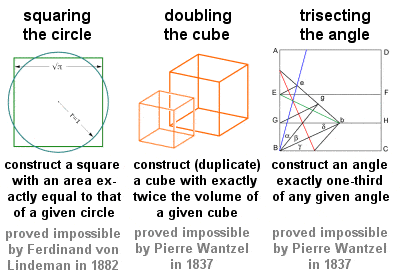
Les trois problèmes classiques
Trois problèmes géométriques en particulier, souvent appelés les trois problèmes classiques, et devant tous être résolus par des moyens purement géométriques en utilisant uniquement une règle et un compas, remontent aux premiers temps de la géométrie grecque : « la quadrature du cercle », « le doublement du cube » et « la trisection d’un angle ». Ces problèmes intransigeants ont profondément influencé la géométrie future et ont conduit à de nombreuses découvertes fructueuses, bien que leurs solutions réelles (ou, comme il s’est avéré, les preuves de leur impossibilité) aient dû attendre jusqu’au 19ème siècle.
Hippocrate de Chios (à ne pas confondre avec le grand médecin grec Hippocrate de Kos. Une biographie détaillée ici.) était l’un de ces mathématiciens grecs qui s’est appliqué à ces problèmes au cours du 5e siècle avant notre ère (sa contribution au problème de la « quadrature du cercle » est connue sous le nom de Lune d’Hippocrate). Son livre influent « Les Éléments », datant d’environ 440 avant notre ère, a été la première compilation des éléments de la géométrie, et son travail a été une source importante pour les travaux ultérieurs d’Euclide.
Paradoxe d’Achille et de la tortue de Zénon
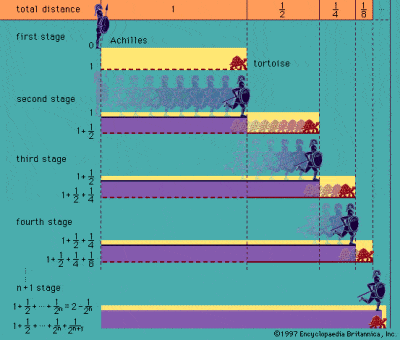
Paradoxe d’Achille et de la tortue de Zénon
Ce sont les Grecs qui ont été les premiers à se débattre avec l’idée de l’infini, telle que décrite dans les paradoxes bien connus attribués au philosophe Zénon d’Élée au Ve siècle avant notre ère. Le plus célèbre de ses paradoxes est celui d’Achille et la tortue, qui décrit une course théorique entre Achille et une tortue. Achille donne à la tortue, beaucoup plus lente, une longueur d’avance, mais lorsqu’Achille atteint le point de départ de la tortue, celle-ci a déjà pris de l’avance. Au moment où Achille atteint ce point, la tortue a encore avancé, etc, etc, de sorte qu’en principe le rapide Achille ne peut jamais rattraper la lente tortue.
Les paradoxes tels que celui-ci et le paradoxe dit de la dichotomie de Zénon sont basés sur la divisibilité infinie de l’espace et du temps, et reposent sur l’idée qu’une moitié plus un quart plus un huitième plus un seizième, etc, etc, à l’infini ne seront jamais tout à fait égaux à un tout. Le paradoxe découle toutefois de l’hypothèse erronée selon laquelle il est impossible de compléter un nombre infini de tirets discrets en un temps fini, bien qu’il soit extrêmement difficile de prouver définitivement ce sophisme. L’ancien Grec Aristote a été le premier de beaucoup à essayer de réfuter les paradoxes, notamment parce qu’il croyait fermement que l’infini ne pouvait jamais être que potentiel et non réel.
Démocrite, le plus célèbre pour ses idées prémonitoires sur le fait que toute matière est composée de minuscules atomes, était également un pionnier des mathématiques et de la géométrie au 5ème – 4ème siècle avant Jésus-Christ, et il a produit des ouvrages portant des titres tels que « Sur les nombres », « Sur la géométrie », « Sur les tangences », « Sur la cartographie » et « Sur les irrationnels », bien que ces ouvrages n’aient pas survécu. Nous savons qu’il a été parmi les premiers à observer qu’un cône (ou une pyramide) a un tiers du volume d’un cylindre (ou d’un prisme) avec la même base et la même hauteur, et il est peut-être le premier à avoir sérieusement considéré la division des objets en un nombre infini de sections transversales.
Cependant, il est certainement vrai que Pythagore en particulier a grandement influencé ceux qui sont venus après lui, y compris Platon, qui a établi sa célèbre Académie à Athènes en 387 avant Jésus-Christ, et son protégé Aristote, dont le travail sur la logique a été considéré comme définitif pendant plus de deux mille ans. Platon le mathématicien est surtout connu pour sa description des cinq solides de Platon, mais la valeur de son travail en tant qu’enseignant et vulgarisateur des mathématiques ne peut être surestimée.
L’élève de Platon, Eudoxe de Cnide, est généralement crédité de la première mise en œuvre de la « méthode d’épuisement » (développée plus tard par Archimède), une première méthode d’intégration par approximations successives qu’il a utilisée pour le calcul du volume de la pyramide et du cône. Il a également développé une théorie générale de la proportion, qui était applicable aux grandeurs incommensurables (irrationnelles) qui ne peuvent pas être exprimées comme un rapport de deux nombres entiers, ainsi qu’aux grandeurs commensurables (rationnelles), étendant ainsi les idées incomplètes de Pythagore.
Peut-être la contribution unique la plus importante des Grecs, cependant – et Pythagore, Platon et Aristote ont tous été influents à cet égard – était l’idée de preuve, et la méthode déductive d’utiliser des étapes logiques pour prouver ou réfuter des théorèmes à partir d’axiomes initiaux supposés. Les cultures plus anciennes, comme celles des Égyptiens et des Babyloniens, s’appuyaient sur le raisonnement inductif, c’est-à-dire sur des observations répétées pour établir des règles empiriques. C’est ce concept de preuve qui donne aux mathématiques leur puissance et garantit que les théories prouvées sont aussi vraies aujourd’hui qu’il y a deux mille ans, et qui a jeté les bases de l’approche systématique des mathématiques d’Euclide et de ceux qui sont venus après lui.
| <<Retour aux mathématiques égyptiennes | Retour à Pythagore >> |
.