Parler en trois dimensions

Regardez cette image d’un prisme rectangulaire:

Combien de sommets a-t-il ? 8

Combien d’arêtes ? 12

Combien de faces ? 6

Facile, non ?

Essayons-en un autre. Regardez cette image d’un cône:

Combien de sommets a-t-il ? Le point au sommet compte-t-il ?

Combien d’arêtes ? Hmm, je ne suis pas sûr. Les arêtes ne sont pas censées être droites ?

Combien de faces ? C’est facile ! Une. Il y a une face circulaire en bas. Mais ce n’est pas un polygone, donc c’est toujours une face ? Oh, et comment dois-je appeler l’autre surface sur le cône ? Les faces ne doivent-elles pas être plates ?

Une question fréquente que nous recevons de la part d’enseignants de 1re, 2e et 3e année porte sur la façon de décrire les attributs de certains solides tridimensionnels, plus précisément les cylindres et les cônes. Selon les TEKS, les élèves sont censés décrire les solides tridimensionnels en utilisant un langage géométrique formel tel que sommet, arête et face. Le problème est que nous essayons d’utiliser un langage qui fonctionne pour une classe de formes pour décrire les attributs d’une classe complètement différente.

Les formes tridimensionnelles comme les prismes et les pyramides sont des polyèdres. « En géométrie, un polyèdre est simplement un solide tridimensionnel qui consiste en une collection de polygones, généralement joints par leurs bords. » (Source) Ces solides ont « des faces polygonales plates, des arêtes droites, et partagent des coins ou des sommets. » (Source)

Les sphères, les cylindres et les cônes, en revanche, ne sont pas des polyèdres. Par conséquent, nous ne pouvons pas utiliser exactement le même langage pour les décrire, ou si nous utilisons le même langage, c’est en comprenant que les définitions ne sont pas identiques. Prenons le mot sommet, par exemple.

Sur un prisme rectangulaire, un sommet est le point net ou le coin où les arêtes se rencontrent. Un prisme rectangulaire a 8 sommets.

Cependant, ce même terme peut aussi être utilisé pour décrire la pointe d’un cône. Même terme, mais pas la même définition. Comme le dit le Dr Math,

La partie vraiment délicate ici est que le « sommet » d’un cône n’a rien à voir avec les arêtes, donc il a besoin d’une toute nouvelle définition ; et je ne peux pas penser à une définition de niveau élémentaire vraiment bonne pour ce qu’ils veulent évidemment dire, qui est simplement un « point ».

A mesure que les élèves poursuivent des mathématiques plus avancées, ils peuvent développer un langage et des définitions plus sophistiqués. En attendant, pendant qu’ils sont à l’école élémentaire, nous utilisons le terme sommet d’un cône dans la RRISD pour décrire cet attribut d’un cône.

Si nous voulons que les élèves décrivent et classent ce type de solide tridimensionnel, alors nous devons fournir un langage accessible à cette fin.

Qu’en est-il des autres attributs d’un cône ? Encore une fois, notre objectif est de fournir un langage accessible aux élèves du primaire et descriptif de ces attributs, en reconnaissant que nos élèves développeront des compréhensions plus formelles plus tard dans leur parcours scolaire. Pour décrire un cône, nous dirons qu’il a une base circulaire, c’est-à-dire la surface plane sur laquelle repose le cône. Nous disons également qu’il a un bord incurvé le long de la base et une surface incurvée qui s’étend de ce bord jusqu’au sommet.

Qu’en est-il d’un cylindre ? Maintenant que nous avons un langage accessible pour décrire les attributs d’un cône, nous pouvons étendre ce langage pour décrire les attributs des cylindres.

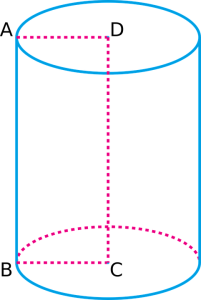
Le cylindre ci-dessus est composé de deux bases circulaires, une en haut et une en bas. Il possède également deux bords courbes, l’un le long du sommet et l’autre le long du fond. Enfin, il possède une surface courbe qui s’étend du bord inférieur jusqu’au bord supérieur.

Je dois ajouter que le cône et le cylindre que j’ai décrits sont tous deux un cône circulaire droit et un cylindre droit. Comme pour les polygones et les polyèdres, il existe de nombreux autres types d’exemples de ces formes. Par exemple, le cône ou le cylindre peuvent être inclinés, ce qui les rend obliques.

Il est important que les élèves voient une variété d’exemples de figures à deux et trois dimensions. Plus ils en rencontrent, plus ils doivent confronter leurs définitions et leur terminologie, ce qui sert à renforcer leur compréhension des attributs et de la façon dont ils nous aident à identifier et à classer ces figures.

Alors, à quoi cela ressemble-t-il dans STAAR ?

Dans le test publié en 2016, STAAR a posé une question qui abordait ce sujet précis et renforçait le vocabulaire que nous utilisons dans RRISD.

La bonne réponse est F Ils n’ont pas de sommets. Si vous regardez l’ensemble B, vous remarquerez qu’il comprend un cône, qui, comme nous l’avons discuté précédemment, a bien un sommet. Si la Texas Education Agency n’utilisait pas le terme sommet d’un cône, alors nous aurions probablement vu le cône inclus dans l’ensemble A.

Voici une pensée finale du Dr Math:

La définition que vous utilisez dépend de ce que vous allez en faire. Si vous ne faites que décrire des objets, ma définition libre convient. Si vous allez prouver des théorèmes impliquant des plans et des angles, vous voudrez vous restreindre à la définition polygonale, mais alors vous ne poserez aucune question sur les cônes. Je pense que les gens ne réalisent souvent pas que, même si nous sommes particuliers sur les définitions en mathématiques, ces définitions varient d’un domaine à l’autre, car elles sont adaptées à un certain contexte. C’est ce que j’essaie de faire ici.