16.3 Stratégies mixtes
Objectif d’apprentissage
- Quels jeux requièrent ou admettent la randomisation comme partie de leur solution ?
Regardons à nouveau le jeu des centimes assortis, tel qu’illustré à la figure 16.13 « Matching pennies again ».
Figure 16.13 Matching pennies again
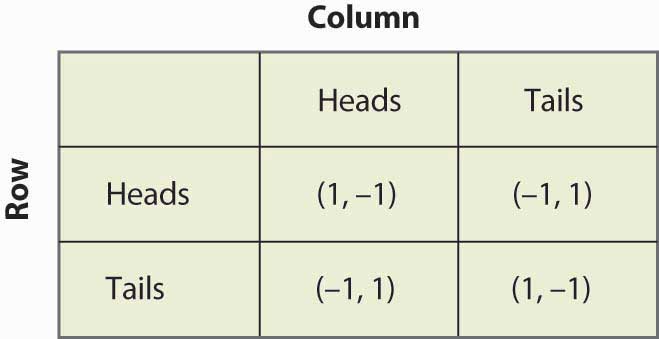
Supposons que Row croit que Column joue Face avec une probabilité p. Alors si Row joue Face, Row obtient 1 avec une probabilité p et -1 avec une probabilité (1 – p), pour une valeur attendue de 2p – 1. De même, si le rang joue face, il obtient -1 avec la probabilité p (lorsque la colonne joue face), et 1 avec la probabilité (1 – p), pour une valeur attendue de 1 – 2p. Ceci est résumé dans la figure 16.14 « Stratégie mixte dans l’appariement des pennies ».
Si 2p – 1 > 1 – 2p, alors Row a intérêt, en moyenne, à jouer Pile que Face. De même, si 2p – 1 < 1 – 2p, alors Row a intérêt à jouer pile que face. Si, par contre, 2p – 1 = 1 – 2p, alors le rang obtient le même gain, quoi qu’il fasse. Dans ce cas, Row pourrait jouer face, pourrait jouer pile, ou pourrait tirer à pile ou face et rendre aléatoire le jeu de Row.
Un équilibre de Nash à stratégie mixteUn équilibre de Nash dans lequel au moins un joueur joue une stratégie aléatoire et aucun joueur n’est capable d’augmenter son gain attendu en jouant une stratégie alternative. implique au moins un joueur jouant une stratégie aléatoire et aucun joueur n’étant capable d’augmenter son gain attendu en jouant une stratégie alternative. Un équilibre de Nash dans lequel aucun joueur ne randomise est appelé équilibre de Nash à stratégie pureUn équilibre de Nash dans lequel aucun joueur ne randomise..
Figure 16.14 Stratégie mixte dans l’appariement des centimes
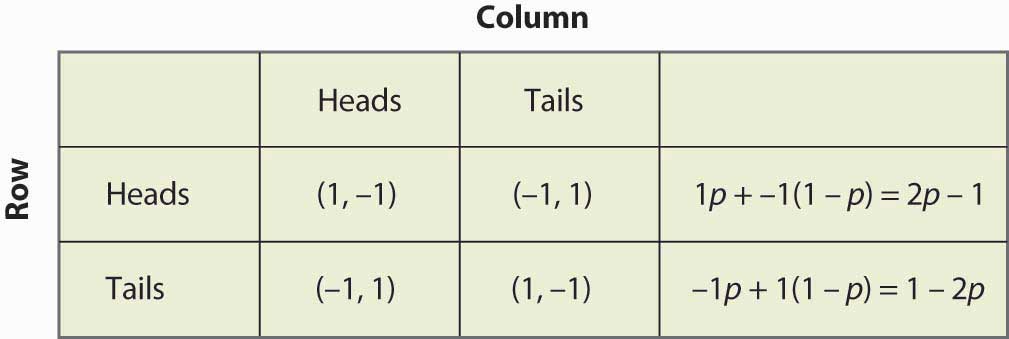
Notez que la randomisation nécessite l’égalité des gains espérés. Si un joueur est censé randomiser sur la stratégie A ou la stratégie B, alors ces deux stratégies doivent produire le même gain attendu. Sinon, le joueur préférerait l’une d’entre elles et ne jouerait pas l’autre.
Le calcul d’une stratégie mixte comporte un élément qui apparaît souvent confus. Supposons que Row va jouer au hasard. Alors les gains de Row doivent être égaux pour toutes les stratégies que Row joue avec une probabilité positive. Mais cette égalité dans les gains de Row ne détermine pas les probabilités avec lesquelles Row joue les différentes rangées. Au contraire, cette égalité dans les gains de Row déterminera les probabilités avec lesquelles Column joue les différentes colonnes. La raison est que ce sont les probabilités de Colonne qui déterminent les gains attendus pour Row ; si Row va randomiser, alors les probabilités de Colonne doivent être telles que Row est prêt à randomiser.
Ainsi, par exemple, nous avons calculé le gain pour Row de jouer Pile, qui était de 2p – 1, où p était la probabilité que Colonne joue Pile. De même, le gain pour Row de jouer Pile est de 1 – 2p. Row est prêt à randomiser si ceux-ci sont égaux, ce qui résout p = ½.
Essayons maintenant un exemple un peu plus difficile et revisitons la bataille des sexes. La figure 16.15 « Stratégie mixte dans la bataille des sexes » illustre à nouveau les gains.
Figure 16.15 Stratégie mixte dans la bataille des sexes
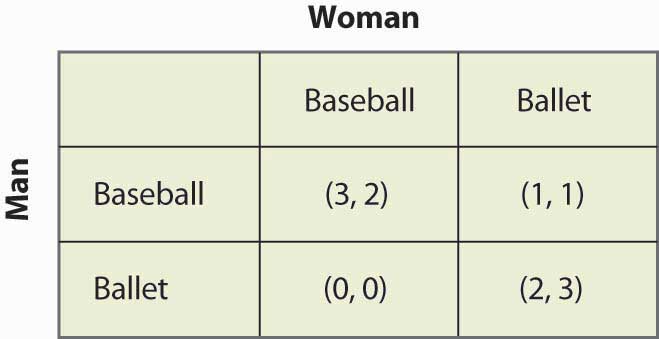
Ce jeu a deux équilibres de Nash en stratégie pure : (Baseball, Baseball) et (Ballet, Ballet). Existe-t-il une stratégie mixte ? Pour calculer une stratégie mixte, laissons la femme aller au jeu de baseball avec la probabilité p, et l’homme aller au jeu de baseball avec la probabilité q. La figure 16.16 « Calcul complet de la stratégie mixte » contient le calcul des gains de la stratégie mixte pour chaque joueur.
Figure 16.16 Calcul complet de la stratégie mixte
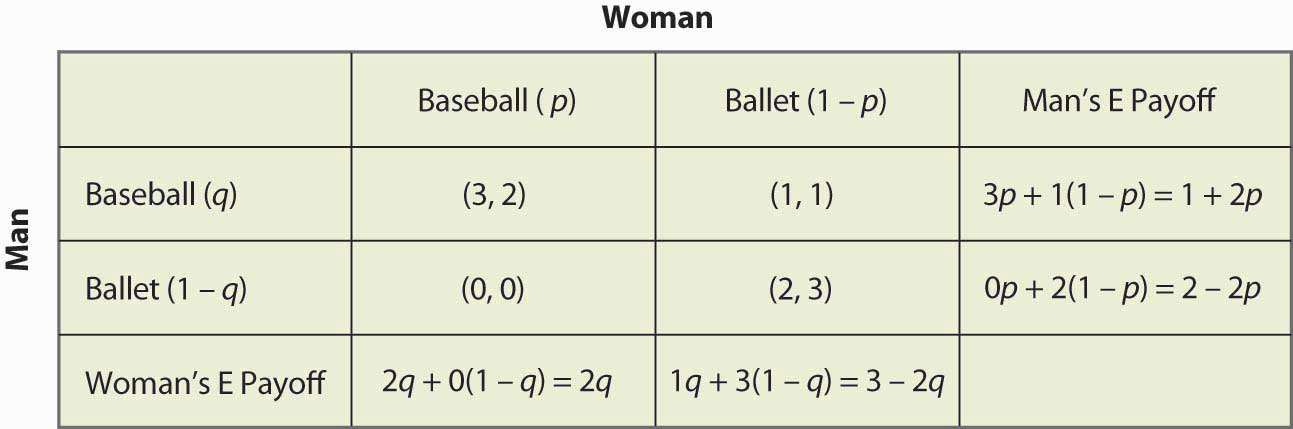
Par exemple, si l’Homme (joueur de ligne) va au match de baseball, il obtient 3 lorsque la Femme va au match de baseball (probabilité p), et sinon obtient 1, pour un gain attendu de 3p + 1(1 – p) = 1 + 2p. Les autres calculs sont similaires, mais vous devez absolument parcourir la logique et vérifier chaque calcul.
Une stratégie mixte dans le jeu de la bataille des sexes nécessite que les deux parties fassent de la randomisation (puisqu’une stratégie pure par l’une des parties empêche la randomisation par l’autre). L’indifférence de l’Homme entre aller au match de baseball et au ballet nécessite 1 + 2p = 2 – 2p, ce qui donne p = ¼. C’est-à-dire que l’Homme sera prêt à randomiser l’événement auquel il assiste si la Femme va au Ballet ¾ du temps, et sinon au match de Baseball. Cela rend l’Homme indifférent entre les deux événements car il préfère être avec la Femme, mais il aime aussi être au match de Baseball. Pour compenser l’avantage que lui procure le jeu, la Femme doit être au Ballet plus souvent.
De même, pour que la Femme soit randomisée, elle doit obtenir des gains égaux en allant au match de Baseball et en allant au Ballet, ce qui nécessite 2q = 3 – 2q, ou q = ¾. Ainsi, la probabilité que l’Homme aille au match de Baseball est ¾, et il va au Ballet ¼ du temps. Ce sont des probabilités indépendantes, donc pour obtenir la probabilité que les deux aillent au match de Baseball, on multiplie les probabilités, ce qui donne 3/16. La figure 16.17 « Probabilités de stratégie mixte » remplit les probabilités pour les quatre résultats possibles.
Figure 16.17 Probabilités de stratégie mixte
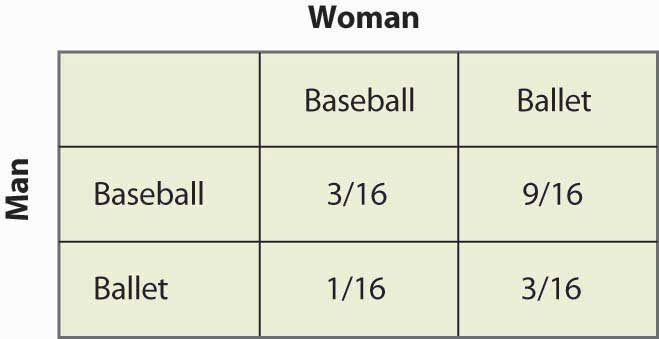
Notez que plus de la moitié du temps (Baseball, Ballet) est le résultat de la stratégie mixte et que les deux personnes ne sont pas ensemble. Ce manque de coordination est généralement une caractéristique des équilibres à stratégie mixte. Les gains attendus des deux joueurs sont également faciles à calculer. Le gain de l’homme est de 1 + 2p = 2 – 2p, et puisque p = ¼, l’homme obtient 1½. Un calcul similaire montre que le gain de la femme est le même. Ainsi, les deux font moins bien que de se coordonner sur leur résultat le moins préféré. Mais cet équilibre de Nash à stratégie mixte, aussi indésirable qu’il puisse paraître, est un équilibre de Nash dans le sens où aucune des parties ne peut améliorer son propre payoff, étant donné le comportement de l’autre partie.
Dans la bataille des sexes, l’équilibre de Nash à stratégie mixte peut sembler improbable ; et nous pourrions nous attendre à ce que le couple se coordonne plus efficacement. En effet, un simple appel téléphonique devrait écarter la stratégie mixte. Considérons donc un autre jeu lié à la bataille des sexes, où l’échec de la coordination est plus logique. Il s’agit du jeu du « poulet ». Dans ce jeu, deux joueurs conduisent l’un vers l’autre, en essayant de convaincre l’autre de céder le passage et de faire une embardée dans un fossé. Si les deux font un écart dans le fossé, nous dirons que le résultat est nul et que les deux obtiennent zéro. Si l’un s’écarte et l’autre pas, le conducteur qui s’écarte perd et l’autre gagne, et nous donnons un point au gagnant.Notez que l’ajout d’une constante aux gains d’un joueur, ou la multiplication des gains de ce joueur par une constante positive, n’affecte pas les équilibres de Nash – purs ou mixtes. Par conséquent, nous pouvons toujours faire en sorte qu’un résultat pour chaque joueur soit égal à zéro et qu’un autre résultat soit égal à un. La seule question qui reste est de savoir ce qui se passe lorsque ni l’un ni l’autre ne cède, auquel cas un crash se produit. Dans cette version, le gain a été fixé à quatre fois la perte de l’embardée, comme le montre la figure 16.18 « Poulet », mais vous pouvez changer le jeu et voir ce qui se passe.
Figure 16.18 Poulet
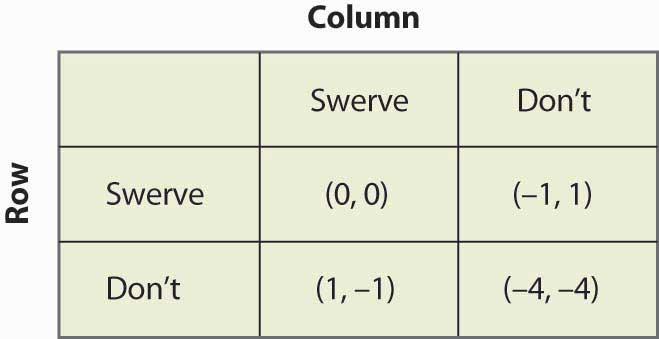
Ce jeu a deux équilibres de stratégie pure : (Swerve, Don’t) et (Don’t, Swerve). En outre, il a une stratégie mixte. Supposons que Colonne s’écarte avec une probabilité p. Alors Row obtient 0p + -1(1 – p) en s’écartant, 1p + (-4)(1 – p) en ne s’écartant pas, et Row randomisera si les deux sont égaux, ce qui nécessite p = ¾. En d’autres termes, la probabilité que Colonne swerve dans un équilibre de stratégie mixte est ¾. Vous pouvez vérifier que le joueur de rang a la même probabilité en fixant la probabilité que Row swerve égale à q et en calculant les gains attendus de Column. Ainsi, la probabilité d’une collision est de 1/16 dans l’équilibre de stratégie mixte.
L’équilibre de stratégie mixte est plus probable, dans un certain sens, dans ce jeu : Si les joueurs savaient déjà qui allait céder, ils n’auraient pas vraiment besoin de jouer le jeu. Le but du jeu est de découvrir qui va céder, ce qui signifie qu’on ne le sait pas à l’avance. Cela signifie que l’équilibre de stratégie mixte est, dans un certain sens, l’équilibre le plus raisonnable.
Figure 16.19 Pierre, papier, ciseaux
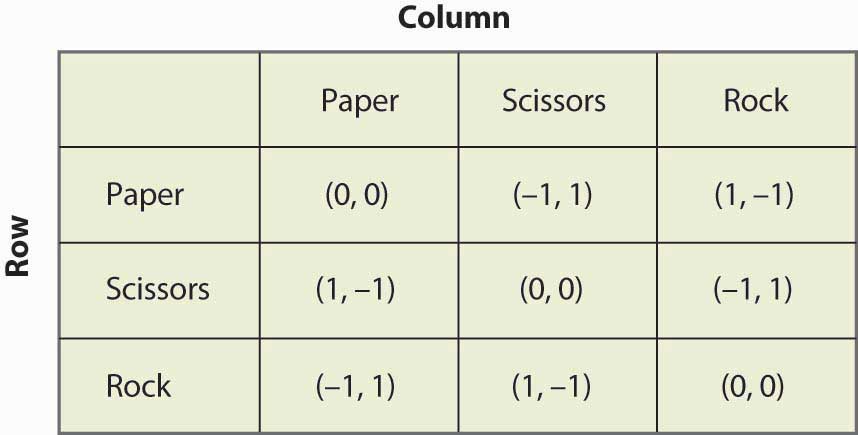
« Pierre, papier, ciseaux » est un jeu d’enfant dans lequel deux enfants utilisent leurs mains pour choisir simultanément du papier (main tenue à plat), des ciseaux (main avec deux doigts qui dépassent pour ressembler à des ciseaux), ou une pierre (main en poing). La nature des gains est la suivante : le papier bat la pierre, la pierre bat les ciseaux et les ciseaux battent le papier. Ce jeu a la structure qui est illustrée dans la figure 16.19 « Pierre, papier, ciseaux ».
Principes clés
- Un équilibre de Nash à stratégie mixte implique qu’au moins un joueur joue une stratégie aléatoire et qu’aucun joueur ne puisse augmenter son gain attendu en jouant une autre stratégie.
- Un équilibre de Nash sans randomisation est appelé équilibre de Nash à stratégie pure.
- Si un joueur est censé randomiser sur deux stratégies, alors les deux doivent produire le même gain espéré.
- Le jeu des centimes assortis a une stratégie mixte et aucune stratégie pure.
- Le jeu de la bataille des sexes a une stratégie mixte et deux stratégies pures.
- Le jeu de la poule est similaire à la bataille des sexes et, comme elle, a deux stratégies pures et une stratégie mixte.
Exercices
- Disons que q est la probabilité que Row joue face. Montrez que Colonne est prêt à randomiser, si et seulement si q = ½. (Indice : calculez d’abord le gain attendu de Colonne lorsque Colonne joue Pile, puis calculez le gain attendu de Colonne lorsque Colonne joue Pile. Ceux-ci doivent être égaux pour que Colonne soit aléatoire.)
- Montrez que dans le jeu pierre, papier, ciseaux, il n’y a pas d’équilibre de stratégie pure. Montrez que jouer les trois actions avec une probabilité égale est un équilibre de stratégie mixte.
-
Trouvez tous les équilibres des jeux suivants :
Figure 16.20
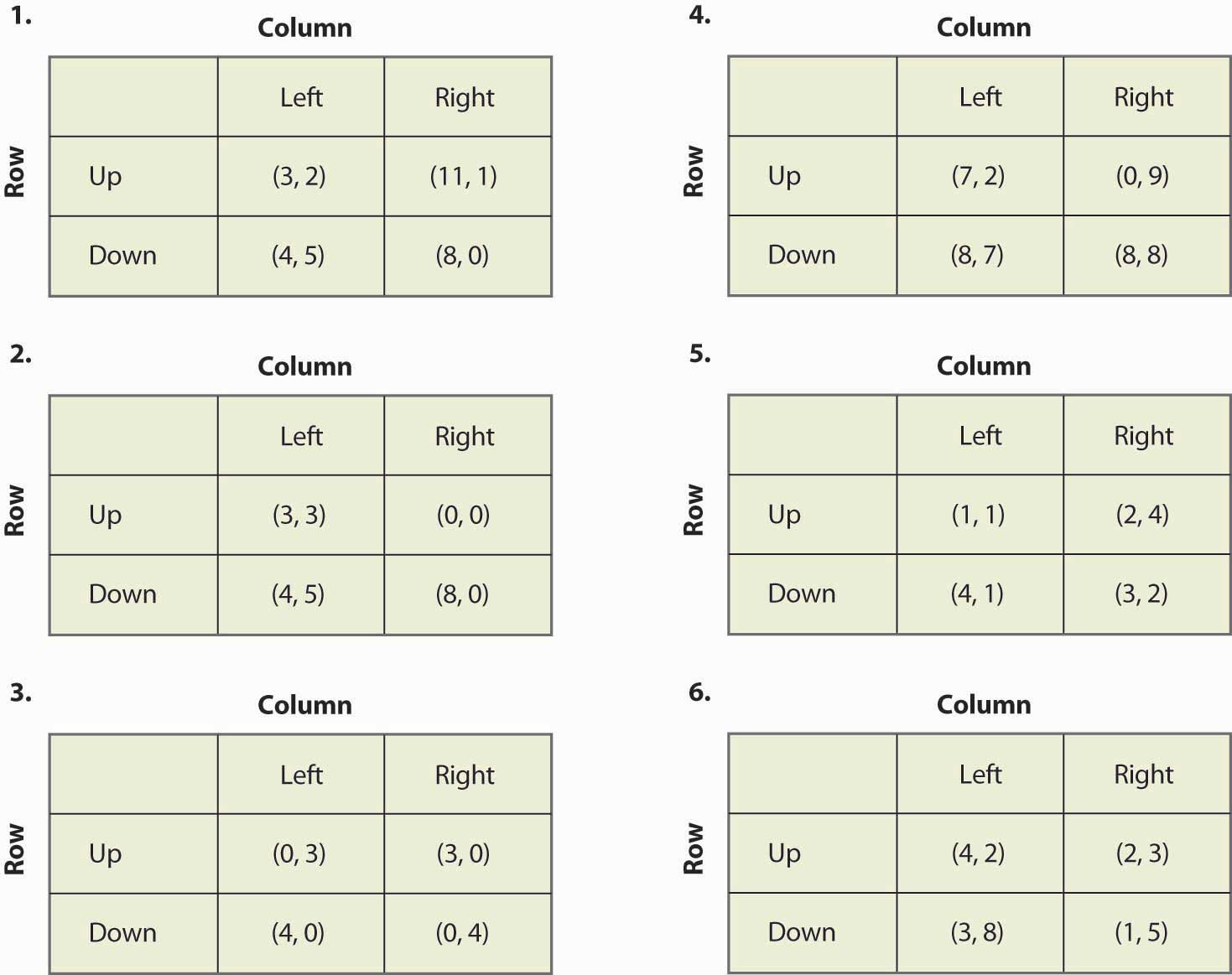
- Si vous multipliez le gain d’un joueur par une constante positive, les équilibres du jeu ne changent pas. Est-ce vrai ou faux, et pourquoi ?