Introduzione
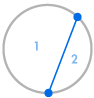
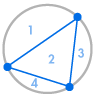
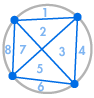
Immaginate di posizionare diversi punti sulla circonferenza di un cerchio e di collegare ogni punto tra loro. Questo divide il cerchio in molte regioni diverse, e possiamo contare il numero di regioni in ogni caso. I diagrammi qui sotto mostrano quante regioni ci sono per diversi numeri di punti sulla circonferenza. Dobbiamo assicurarci che solo due linee si incontrino ad ogni intersezione all’interno del cerchio, non tre o più.
 |
 |
 |
 |
 |
| 1 regione | 2 regioni | 4 regioni | 8 regioni | 16 regioni |
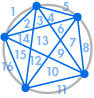
Si vede subito uno schema: il numero di regioni è sempre il doppio del precedente, in modo da ottenere la sequenza 1, 2, 4, 8, 16, … Ciò significa che con 6 punti sulla circonferenza ci sarebbero 32 regioni, e con 7 punti ci sarebbero 64 regioni.
Potremmo decidere che siamo soddisfatti di questo risultato. Il numero di regioni è sempre il doppio del precedente – dopo tutto questo ha funzionato per i primi cinque casi. Oppure potremmo decidere che dovremmo controllarne altre, giusto per essere sicuri:
 |
 |
| 31 regioni, non 32 | 57 regioni, non 64 |
Purtroppo qualcosa è andato storto: 31 potrebbe sembrare un errore di conteggio, ma 57 è molto meno di 64. La sequenza continua 99, 163, 256, …, molto diversa da quella che otterremmo raddoppiando il numero precedente.
Questo esempio illustra perché, in matematica, non si può semplicemente dire che un’osservazione è sempre vera solo perché funziona in alcuni casi che abbiamo testato. Bisogna invece elaborare un’argomentazione logica rigorosa che porti da risultati che già si conoscono a qualcosa di nuovo che si vuole dimostrare essere vero. Un argomento del genere si chiama prova.
Le prove sono ciò che rende la matematica diversa da tutte le altre scienze, perché una volta che abbiamo dimostrato qualcosa siamo assolutamente certi che è e sarà sempre vera. Non è solo una teoria che si adatta alle nostre osservazioni e può essere sostituita da una teoria migliore in futuro.
Nell’esempio precedente, potremmo contare il numero di intersezioni all’interno del cerchio. Pensando attentamente alla relazione tra il numero di intersezioni, linee e regioni, alla fine ci porterà ad una diversa equazione per il numero di regioni quando ci sono x = V.Axi sul cerchio:
Numero di regioni = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Questa equazione funziona in tutti i casi precedenti. Potremmo ora provare a provarla per ogni valore di x usando “l’induzione”, una tecnica spiegata più avanti.
Tradizionalmente, la fine di una dimostrazione è indicata usando una ■ o □, o scrivendo QED o “quod erat demonstrandum”, che è latino per “ciò che doveva essere dimostrato”.
Un risultato o un’osservazione che pensiamo sia vera è chiamata Ipotesi o Congettura. Una volta che l’abbiamo dimostrato, lo chiamiamo Teorema. Una volta dimostrato un teorema, possiamo usarlo per dimostrare altri risultati più complicati – costruendo così una rete crescente di teoremi matematici.
Axiomi

Scuola di Atene di Raffaello: gli antichi matematici greci furono i primi ad avvicinarsi alla matematica usando una struttura logica e assiomatica.
Una domanda interessante è da dove iniziare. Come si fa a dimostrare il primo teorema, se non si sa ancora nulla? Purtroppo non si può dimostrare qualcosa usando il nulla. Hai bisogno di almeno alcuni elementi di base da cui partire, e questi si chiamano Assiomi.
I matematici assumono che gli assiomi siano veri senza essere in grado di dimostrarli. Tuttavia questo non è così problematico come può sembrare, perché gli assiomi sono o definizioni o chiaramente ovvie, e ci sono solo pochi assiomi. Per esempio, un assioma potrebbe essere che a + b = b + a per qualsiasi due numeri a e b.
Gli assiomi sono importanti per essere corretti, perché tutta la matematica si basa su di essi. Se ci sono troppo pochi assiomi, si può dimostrare molto poco e la matematica non sarebbe molto interessante. Se ci sono troppi assiomi, si può dimostrare quasi tutto, e anche la matematica non sarebbe interessante. Inoltre non si possono avere assiomi che si contraddicono l’un l’altro.
La matematica non consiste nello scegliere il giusto insieme di assiomi, ma nello sviluppare un quadro di riferimento da questi punti di partenza. Se si parte da assiomi diversi, si otterrà un tipo diverso di matematica, ma gli argomenti logici saranno gli stessi. Ogni area della matematica ha il suo insieme di assiomi di base.
Quando i matematici hanno dimostrato un teorema, lo pubblicano perché altri matematici lo controllino. A volte trovano un errore nell’argomentazione logica, e a volte un errore non viene trovato fino a molti anni dopo. Tuttavia, in linea di principio, è sempre possibile scomporre una dimostrazione negli assiomi di base.
Teoria degli insiemi e l’assioma della scelta

Per formulare le dimostrazioni è talvolta necessario risalire al fondamento stesso del linguaggio in cui è scritta la matematica: la teoria degli insiemi.
Un insieme è una collezione di oggetti, come i numeri. Gli elementi di un insieme sono di solito scritti tra parentesi graffe. Possiamo trovare l’unione di due insiemi (l’insieme degli elementi che sono in uno dei due insiemi) o possiamo trovare l’intersezione di due insiemi (l’insieme degli elementi che sono in entrambi gli insiemi).
Molti problemi matematici possono essere formulati nel linguaggio della teoria degli insiemi, e per dimostrarli abbiamo bisogno degli assiomi della teoria degli insiemi. Nel corso del tempo, i matematici hanno utilizzato diverse collezioni di assiomi, il più ampiamente accettato è costituito dai nove assiomi di Zermelo-Fraenkel (ZF):
ASSIOMI DI ESTENSIONE
Se due insiemi hanno gli stessi elementi, allora sono uguali.
ASSIMO DI SEPARAZIONE
Possiamo formare un sottoinsieme di un insieme, che consiste di alcuni elementi.

ASSIEME DI SET
C’è un insieme senza membri, scritto come {} o ∅.
ASSEMO DEI PAIR-SET
Dati due oggetti x e y possiamo formare un insieme {x, y}.
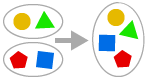
ASSEMO DI UNIONE
Possiamo formare l’unione di due o più insiemi.
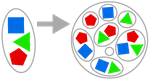
ASSEMO DI POTENZA
Dato un qualsiasi insieme, possiamo formare l’insieme di tutti i sottoinsiemi (l’insieme di potenza).
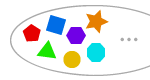
ASSEMO DELL’INFINITÀ
C’è un insieme con infiniti elementi.

AXIOM DELLA FONDAZIONE
Gli insiemi sono costruiti a partire da insiemi più semplici, il che significa che ogni insieme (non vuoto) ha un membro minimo.
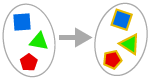
ASSIOMA DELLA SOSTITUZIONE
Se applichiamo una funzione ad ogni elemento di un insieme, la risposta è ancora un insieme.
Se si pensa alla teoria degli insiemi, la maggior parte di questi assiomi sembrerà completamente ovvia – e questo è ciò che gli assiomi dovrebbero essere. Tuttavia c’è un decimo assioma che è un po’ più problematico:
ASSIOMA DELLA SCELTA
Dati infiniti insiemi non vuoti, si può scegliere un elemento da ciascuno di questi insiemi.
A prima vista, l’assioma della scelta (AC) sembra innocente come gli altri precedenti. Tuttavia l’uso dell’infinito ha una serie di conseguenze inaspettate. Per esempio, si può usare l’AC per dimostrare che è possibile tagliare una sfera in cinque pezzi e riassemblarli per fare due sfere, ciascuna identica alla sfera iniziale. Questo è solo un concetto teorico – i tagli richiesti sono frattali, il che significa che non possono esistere realmente nella vita reale, e alcuni dei pezzi sono “non misurabili”, il che significa che non hanno un volume definito. Ma il fatto che l’assioma della scelta possa essere usato per costruire questi tagli impossibili è abbastanza preoccupante.
C’è un dibattito appassionato tra i logici, se accettare o meno l’assioma della scelta. Ogni collezione di assiomi forma un piccolo “mondo matematico”, e teoremi diversi possono essere veri in mondi diversi. In realtà è solo una questione se si è felici di vivere in un mondo in cui si possono fare due sfere da una…
Prova per induzione
La prova per induzione è una tecnica che può essere usata per dimostrare che una certa affermazione è vera per tutti i numeri naturali 1, 2, 3, … L'”affermazione” è di solito un’equazione o formula che include una variabile n che potrebbe essere qualsiasi numero naturale. Denotiamo l’affermazione applicata a n con S(n). Ecco i quattro passi dell’induzione matematica:
- Prima proviamo che S(1) è vero, cioè che l’enunciato S è vero per 1.
- Ora assumiamo che S(k) sia vero, cioè che l’enunciato S sia vero per qualche numero naturale k.
- Utilizzando questo assunto, proviamo a dedurre che anche S(k + 1) è vero. Così ogni volta che S è vero per un numero è vero anche per il numero successivo.
- Siccome sappiamo che S(1) è vero, S(2) deve essere vero. E quindi S(3) deve essere vera. E quindi S(4) deve essere vero. E così via: S deve essere vero per tutti i numeri.

L’induzione può essere paragonata alle tessere del domino che cadono: ogni volta che una tessera cade, cade anche la successiva. Il primo passo, dimostrare che S(1) è vero, avvia la reazione a catena infinita.
Il primo passo è spesso trascurato, perché è così semplice. In realtà è molto importante e l’intera catena di induzione dipende da esso – come alcuni degli esempi seguenti mostreranno…
L’obiettivo del gioco delle Torri di Hanoi è di spostare un certo numero di dischi da un piolo all’altro. Puoi spostare solo un disco alla volta e non puoi mettere un disco più grande sopra uno più piccolo. Cerca di spostare la torre di dischi dal primo all’ultimo piolo, con il minor numero di mosse possibile:
Numero di dischi: Start Over Moves: 0
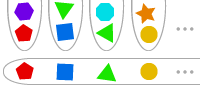
Una volta che abbiamo capito le regole del gioco, possiamo cercare di trovare il minor numero di passi necessari, dato qualsiasi numero di dischi. Giocare con il gioco di cui sopra potrebbe portarci ad osservare che, con n dischi, sono necessari almeno 2n – 1 passi. Chiamiamo questa affermazione S(n).
S(1) è chiaramente vera poiché, con un solo disco, hai bisogno di una sola mossa, e 21 – 1 = 1.
Assumiamo ora che S(k) sia vera, cioè che hai bisogno di 2k – 1 passi per k dischi. Allora se abbiamo k + 1 dischi:
In totale abbiamo bisogno di (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 passi. Questo significa che anche S(k + 1) è vero.
Per induzione matematica, S(n) è vero per tutti i valori di n, il che significa che il modo più efficiente per spostare n = V.Hanoi dischi richiede 2n – 1 = Math.pow(2,V.Hanoi)-1 mosse. ■
Utilizziamo l’induzione per dimostrare che la somma dei primi n numeri naturali è n (n + 1)2. Controlliamo prima l’equazione per piccoli valori di n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
In seguito, assumiamo che il risultato sia vero per k, cioè che 1 + 2 + … + k = k (k + 1)2, dove k è qualche numero che non specifichiamo. Ora
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Abbiamo appena dimostrato che se l’equazione è vera per qualche k, allora è vera anche per k + 1. Per induzione matematica, l’equazione è vera per tutti i valori di n. ■
C’è un altro modo intelligente per dimostrare l’equazione di cui sopra, che non usa l’induzione. Si dice che Carl Friedrich Gauss (1777 – 1855), uno dei più grandi matematici della storia, abbia scoperto questo metodo alle elementari, quando il suo insegnante gli chiese di sommare tutti i numeri interi da 1 a 100.
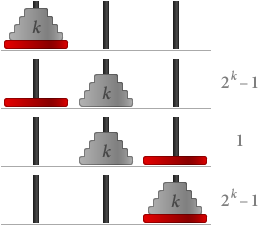
Utilizzando l’induzione, vogliamo dimostrare che tutti gli esseri umani hanno lo stesso colore di capelli. Sia S(n) l’affermazione che “qualsiasi gruppo di n esseri umani ha lo stesso colore di capelli”.
E’ chiaro che S(1) è vero: in qualsiasi gruppo di uno solo, tutti hanno lo stesso colore di capelli.
Assumiamo ora S(k), che in qualsiasi gruppo di k tutti hanno lo stesso colore di capelli. Se sostituiamo uno qualsiasi del gruppo con un altro, fanno ancora un totale di k e quindi hanno lo stesso colore di capelli. Questo funziona per qualsiasi gruppo iniziale di persone, il che significa che qualsiasi gruppo di k + 1 ha anche lo stesso colore di capelli. Quindi S(k + 1) è vero.
Per induzione matematica, tutti gli esseri umani hanno lo stesso colore di capelli! ■
E’ chiaro che qualcosa deve essere andato storto nella dimostrazione di cui sopra – dopo tutto, non tutti hanno lo stesso colore di capelli. Puoi trovare l’errore?
Alcuni teoremi non possono essere dimostrati usando l’induzione – dobbiamo usare una versione leggermente modificata chiamata Induzione Forte. Invece di assumere S(k) per provare S(k + 1), assumiamo tutto S(1), S(2), … S(k) per provare S(k + 1). Tutto ciò che può essere dimostrato usando l’induzione (debole) può chiaramente essere dimostrato anche usando l’induzione forte, ma non viceversa.
Il teorema fondamentale dell’aritmetica afferma che ogni numero intero maggiore di 1 è un numero primo, o può essere scritto come prodotto di numeri primi in modo essenzialmente unico.
Possiamo dimostrare parti di esso usando l’induzione forte: sia S(n) l’affermazione che “l’intero n è un primo o può essere scritto come prodotto di numeri primi”. S(1) è un’eccezione, ma S(2) è chiaramente vero perché 2 è un numero primo.
Ora assumiamo che S(1), S(2), …, S(k) siano tutti veri, per qualche numero intero k. Sappiamo che k + 1 è un numero primo o ha fattori minori di k + 1. Per la nostra assunzione, sappiamo che questi fattori possono essere scritti come il prodotto di numeri primi. Pertanto, a meno che non sia primo, k + 1 può anche essere scritto come prodotto di numeri primi. Questo significa che S(k + 1) è vero.
Per induzione forte, S(n) è vero per tutti i numeri n maggiori di 1. ■
Provare che questa fattorizzazione primaria è unica (a meno che non si contino diversi ordinamenti dei fattori) richiede più lavoro, ma non è particolarmente difficile.
Si scopre che il principio di induzione debole e il principio di induzione forte sono equivalenti: ognuno implica l’altro. Sono anche entrambi equivalenti a un terzo teorema, il principio del buon ordine: qualsiasi insieme (non vuoto) di numeri naturali ha un elemento minimo, più piccolo di tutti gli altri.
Il principio del buon ordine è la caratteristica che definisce i numeri naturali. È uno degli assiomi di base usati per definire i numeri naturali ![]() = {1, 2, 3, …}. Questi assiomi sono chiamati Assiomi di Peano, dal nome del matematico italiano Giuseppe Peano (1858 – 1932).
= {1, 2, 3, …}. Questi assiomi sono chiamati Assiomi di Peano, dal nome del matematico italiano Giuseppe Peano (1858 – 1932).
Prova per contraddizione
La prova per contraddizione è un’altra importante tecnica di prova. Se vogliamo provare un’affermazione S, assumiamo che S non sia vera. Usando questa assunzione cerchiamo di dedurre un risultato falso, come 0 = 1. Se tutti i nostri passi sono stati corretti e il risultato è falso, la nostra assunzione iniziale deve essere stata sbagliata. La nostra assunzione iniziale era che S non è vera, il che significa che S è effettivamente vera.
Questa tecnica può essere usata in molte circostanze diverse, come dimostrare che √2 è irrazionale, dimostrare che i numeri reali non sono numerabili, o dimostrare che ci sono infiniti numeri primi.
Ecco un altro esempio divertente:
Possiamo usare la prova per contraddizione, insieme al principio del buon ordine, per dimostrare che tutti i numeri naturali sono “interessanti”.
Supponiamo che non tutti i numeri naturali siano interessanti, e che S sia l’insieme dei numeri non interessanti. Per il principio del ben ordinare, S ha un membro più piccolo x che è il più piccolo numero non interessante. Questa curiosa proprietà rende chiaramente x un numero particolarmente interessante. Questa è una contraddizione perché abbiamo assunto che x fosse non interessante.
Quindi tutti i numeri sono interessanti.
Gödel e i teoremi indimostrabili

Kurt Gödel (1906-1978)
All’inizio del XX secolo, la matematica iniziò a crescere rapidamente, con migliaia di matematici che lavoravano in innumerevoli nuove aree. David Hilbert (1862 – 1943) mise in piedi un vasto programma per formalizzare la matematica e per risolvere qualsiasi incongruenza nei fondamenti della matematica. Ciò includeva dimostrare tutti i teoremi usando un insieme di assiomi semplici e universali, dimostrare che questo insieme di assiomi è coerente, e dimostrare che questo insieme di assiomi è completo, cioè che ogni affermazione matematica può essere dimostrata o confutata usando gli assiomi.
Purtroppo, questi piani furono distrutti da Kurt Gödel nel 1931. Egli dimostrò che in qualsiasi sistema matematico (sufficientemente complesso) con un certo insieme di assiomi, è possibile trovare alcune affermazioni che non possono essere né dimostrate né confutate usando quegli assiomi. Non è nemmeno possibile dimostrare che un certo insieme di assiomi è coerente, usando nient’altro che gli assiomi stessi.
La scoperta di Gödel si basa sul fatto che un insieme di assiomi non può essere usato per dire qualcosa su se stesso, come se è coerente. I problemi di autoreferenzialità non si trovano solo in matematica, ma anche nel linguaggio. Ecco il Paradosso del Bugiardo:
“Questa frase è falsa”
La frase sopra cerca di dire qualcosa su se stessa. Se è vera, allora la frase ci dice che è falsa. Se è falsa, allora la frase ci dice che non è falsa, cioè che è vera. In effetti, la frase non è né vera né falsa.
Quando furono pubblicati per la prima volta, i teoremi di Gödel preoccuparono profondamente molti matematici. Quando ci si accinge a dimostrare un’osservazione, non si sa se esiste una prova – il risultato potrebbe essere vero ma non dimostrabile. Oggi sappiamo che l’incompletezza è una parte fondamentale non solo della logica ma anche dell’informatica, che si basa su macchine che eseguono operazioni logiche.
Sorprendentemente, è possibile dimostrare che certe affermazioni non sono dimostrabili. Un esempio è l’Ipotesi del Continuo, che riguarda la dimensione degli insiemi infiniti.
Verso la fine della sua vita, Kurt Gödel sviluppò gravi problemi mentali e morì di inedia nel 1978. Le sue intuizioni sui fondamenti della logica sono state le più profonde dopo lo sviluppo della dimostrazione da parte degli antichi greci.