
Bertrand Russell (1872-1970) e A.N. Whitehead (1861-1947)
Bertrand Russell e Alfred North Whitehead erano matematici, logici e filosofi britannici, che furono all’avanguardia della rivolta britannica contro l’idealismo continentale all’inizio del XX secolo e, insieme, diedero importanti contributi nei campi della logica matematica e della teoria degli insiemi.
Whitehead era il maggiore dei due e veniva da un background di matematica pura. Divenne il tutor di Russell al Trinity College di Cambridge negli anni 1890, e poi collaborò con il suo più celebre ex-allievo nel primo decennio del XX secolo per la loro opera monumentale, i “Principia Mathematica”. Dopo la prima guerra mondiale, però, gran parte della quale Russell trascorse in prigione a causa delle sue attività pacifiste, la collaborazione si spense, e la carriera accademica di Whitehead rimase sempre all’ombra di quella del più fiammeggiante Russell. Emigrò negli Stati Uniti negli anni venti e vi trascorse il resto della sua vita.
Russell nacque in una ricca famiglia dell’aristocrazia britannica, anche se i suoi genitori erano estremamente liberali e radicali per l’epoca. I suoi genitori morirono quando Russell era abbastanza giovane ed egli fu in gran parte cresciuto dalla nonna, di stampo prettamente vittoriano (anche se abbastanza progressista). La sua adolescenza fu molto solitaria e soffrì di attacchi di depressione, affermando in seguito che fu solo il suo amore per la matematica a trattenerlo dal suicidio. Studiò matematica e filosofia all’Università di Cambridge sotto G.E. Moore e A.N. Whitehead, dove divenne un filosofo innovativo, uno scrittore prolifico su molti argomenti, un ateo impegnato e un matematico e logico ispirato. Oggi è considerato uno dei fondatori della filosofia analitica, ma ha scritto su quasi tutte le principali aree della filosofia, in particolare la metafisica, l’etica, l’epistemologia, la filosofia della matematica e la filosofia del linguaggio.
Russell fu un attivista politico impegnato e di alto profilo durante la sua lunga vita. Fu un importante attivista contro la guerra durante la prima e la seconda guerra mondiale, sostenne il libero scambio e l’antimperialismo, e più tardi divenne uno stridente sostenitore del disarmo nucleare e del socialismo, e contro Adolf Hitler, il totalitarismo sovietico e il coinvolgimento degli USA nella guerra del Vietnam.
Il paradosso di Russell
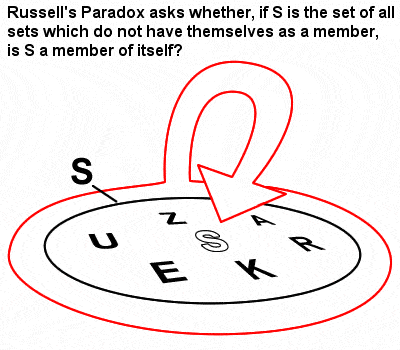
Il paradosso di Russell
La matematica di Russell fu fortemente influenzata dalla teoria degli insiemi e dal logicismo che Gottlob Frege aveva sviluppato sulla scia dei primi lavori rivoluzionari di Cantor sugli insiemi. Nel suo “The Principles of Mathematics” del 1903, tuttavia, identificò quello che è diventato noto come il paradosso di Russell (un insieme contenente insiemi che non sono membri di se stessi), che mostrava che la teoria ingenua degli insiemi di Frege poteva in effetti portare a contraddizioni.
Il paradosso è talvolta illustrato da questo esempio semplicistico: “Se un barbiere rade tutti e solo gli uomini del villaggio che non si radono da soli, si rade da solo?”
Il paradosso sembrava implicare che i fondamenti stessi di tutta la matematica non potevano più essere affidabili, e che, anche in matematica, la verità non poteva mai essere conosciuta in modo assoluto (il lavoro successivo di Gödel e Turing avrebbe solo peggiorato la situazione). La critica di Russell fu sufficiente a far vacillare la fiducia di Frege nell’intero edificio del logicismo, ed egli fu abbastanza cortese da ammetterlo apertamente in un’appendice frettolosamente scritta al volume II delle sue “Leggi fondamentali dell’aritmetica”.
Ma l’opus magnum di Russell fu il monolitico “Principia Mathematica”, pubblicato in tre volumi nel 1910, 1912 e 1913. Il primo volume fu co-scritto da Whitehead, anche se i due successivi furono quasi tutti opera di Russell. L’aspirazione di questo ambizioso lavoro non era altro che un tentativo di derivare tutta la matematica da assiomi puramente logici, evitando i tipi di paradossi e contraddizioni che si trovano nel precedente lavoro di Frege sulla teoria degli insiemi. Russell raggiunse questo obiettivo impiegando una teoria o un sistema di “tipi”, per cui ogni entità matematica è assegnata a un tipo all’interno di una gerarchia di tipi, in modo che gli oggetti di un dato tipo siano costruiti esclusivamente da oggetti di tipi precedenti più bassi nella gerarchia, impedendo così i loop. Ogni insieme di elementi, quindi, è di un tipo diverso da ciascuno dei suoi elementi, in modo che non si possa parlare di “insieme di tutti gli insiemi” e costrutti simili, che portano a paradossi.
Tuttavia, i “Principia” richiedevano, oltre agli assiomi di base della teoria dei tipi, altri tre assiomi che sembravano non essere veri come semplici questioni di logica, cioè l'”assioma dell’infinito” (che garantisce l’esistenza di almeno un insieme infinito, cioè l’insieme di tutti i numeri naturali), l'”assioma della scelta” (che assicura che, data una qualsiasi collezione di “bidoni”, ciascuno contenente almeno un oggetto, è possibile fare una selezione di esattamente un oggetto da ogni cestino, anche se ci sono infiniti cestini, e che non c’è una “regola” per quale oggetto scegliere da ciascuno) e lo stesso “assioma di riducibilità” di Russell (che afferma che qualsiasi funzione di verità proposizionale può essere espressa da una funzione di verità predicativa formalmente equivalente).
Durante i circa dieci anni che Russell e Whitehead trascorsero sui “Principia”, una bozza dopo l’altra fu iniziata e abbandonata mentre Russell ripensava costantemente le sue premesse di base. Russell e sua moglie Alys si trasferirono addirittura dai Whitehead per accelerare il lavoro, anche se il suo matrimonio ne risentì perché Russell si infatuò della giovane moglie di Whitehead, Evelyn. Alla fine, Whitehead insistette per la pubblicazione dell’opera, anche se non era (e potrebbe non essere mai) completa, anche se furono costretti a pubblicarla a proprie spese perché nessun editore commerciale l’avrebbe toccata.
Principia Mathematica

Una piccola parte della lunga prova che 1+1 =2 nei “Principia Mathematica”
Qualche idea della portata e della completezza dei “Principia” può essere ricavata dal fatto che ci vogliono più di 360 pagine per dimostrare definitivamente che 1 + 1 = 2.
Oggi, è ampiamente considerato come una delle opere più importanti e seminali nella logica dopo l'”Organon” di Aristotele. Sembrava notevolmente riuscito e resistente nei suoi ambiziosi obiettivi, e presto guadagnò la fama mondiale di Russell e Whitehead. Infatti, fu solo il teorema di incompletezza di Gödel del 1931 a dimostrare finalmente che i “Principia” non potevano essere sia coerenti che completi.
Russell fu insignito dell’Ordine al Merito nel 1949 e del Premio Nobel per la letteratura l’anno successivo. La sua fama continuò a crescere, anche al di fuori dei circoli accademici, e divenne qualcosa di familiare in età avanzata, anche se in gran parte come risultato dei suoi contributi filosofici e del suo attivismo politico e sociale, che continuò fino alla fine della sua lunga vita. Morì di influenza nel suo amato Galles alla grande età di 97 anni.
| << Torna a Hardy e Ramanujan | Avanti a Hilbert >> |