What is a Lattice?
Un reticolo è un array ordinato di punti che descrive la disposizione delle particelle che formano un cristallo.
La cella unitaria di un cristallo è definita dai punti del reticolo.La cella unitaria è la più piccola parte di un cristallo che ripetuta regolarmente attraverso la traslazione in tre dimensioni crea l’intero cristallo.
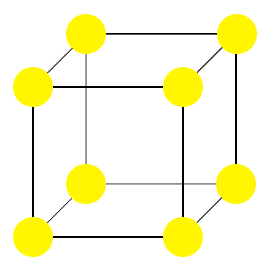
Per esempio, l’immagine mostrata qui è la cella unitaria di una struttura cubica primitiva.
Nella struttura disegnata, tutte le particelle (gialle) sono uguali.In questo caso particolare, i punti del reticolo che definiscono la cella unitaria coincidono con i centri delle particelle del cristallo. Questo non deve essere sempre il caso.
Il reticolo ionico
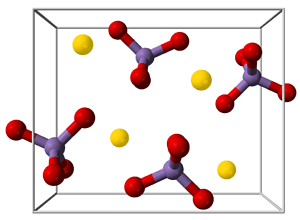
Se un cristallo è formato da ioni, il composto può essere descritto come un reticolo ionico.
Ben noti esempi di reticoli ionici sono il cloruro di sodio, il permanganato di potassio, il borace (borato di sodio) e il solfato di rame (II).

Il reticolo covalente
Se un cristallo è composto da atomi legati covalentemente, può essere descritto come un reticolo covalente o reticolo covalente infinito.
Ben noti esempi di reticoli covalenti sono il diamante, il quarzo (biossido di silicio), il silicio e lo stagno grigio.
Costanti di reticolo
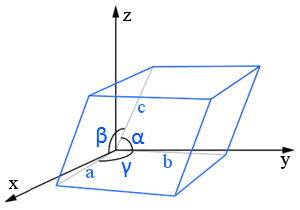
Le costanti di reticolo (o parametri di reticolo) sono le lunghezze e gli angoli tra i bordi della cella unitaria.
In questo diagramma di reticolo parallelepipedo, le costanti di reticolo sono a, b, e c (lunghezze) e α, β, e γ (angoli).
Strutture di reticolo
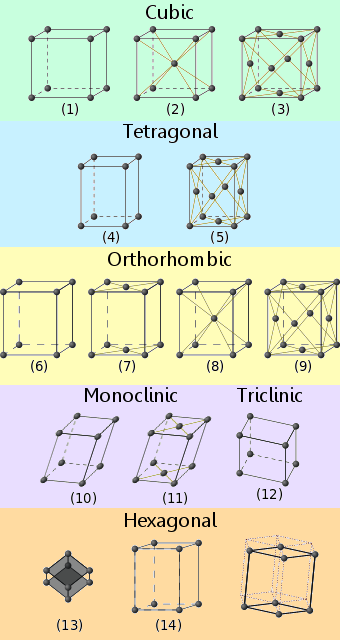
I materiali cristallini rientrano in uno dei quattordici schemi di reticolo riconosciuti, noti come reticoli di Bravais.
I nomi dei sistemi di reticolo cristallino, corrispondenti ai numeri sui diagrammi, sono i seguenti:
1. Cubico primitivo
2. Cubico centrato sul corpo
3. Cubico centrato sulla faccia
4. Tetragonale primitivo
5. Tetragonale centrato sul corpo
6. Ortorombico primitivo
7. Ortorombico centrato sulla base
8. Ortorombico centrato sul corpo
9. Ortorombico centrato sulla faccia
10. Primitivo monoclino
11. Monoclino centrato alla base
12. Triclino
13. Romboedrico
14. Esagonale
Difetti del reticolo
Se si assumesse che un cristallo sia basato su un reticolo ionico matematicamente perfetto, la sua resistenza alla trazione calcolata sarebbe molto maggiore di quella effettivamente osservata.