Il metodo Delta-Delta Ct o metodo Livak è il metodo preferito per l’analisi dei dati qPCR. Tuttavia, può essere usato solo quando sono soddisfatti certi criteri, si prega di fare riferimento alle note della lezione per assicurarsi che questi criteri siano soddisfatti. In caso contrario, il metodo più generalizzato è chiamato metodo Pfaffl. Si prega di leggere il materiale di lettura aggiuntivo per ottenere maggiori informazioni su questo metodo.
Qui ci sono i passi per il metodo Livak:
Il file Excel con tutti i calcoli sono nella cartella di analisi qPCR su Blackboard.
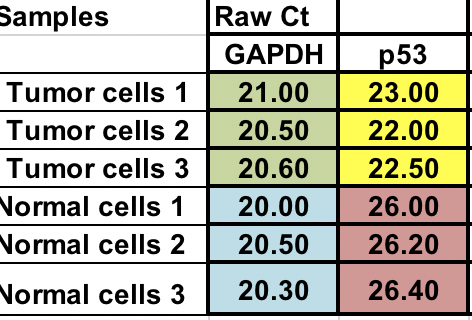
Hai il Ct grezzo (numero di cicli che impiega per raggiungere la soglia) per le cellule normali e tumorali (3 replicati per ciascuno).
Normalizzazione¶
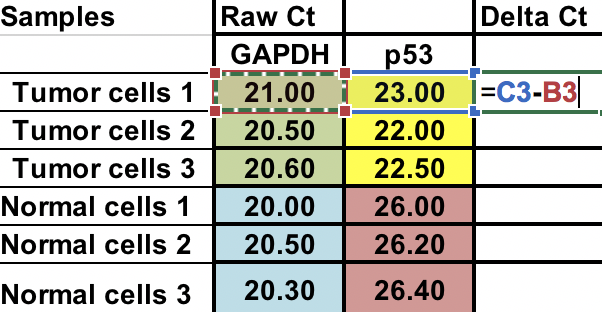
Prima, dovrai calcolare la differenza relativa tra il gene di interesse (p53) e il gene di mantenimento (GAPDH).
∆Ct = Ct (gene di interesse) – Ct (gene housekeeping)
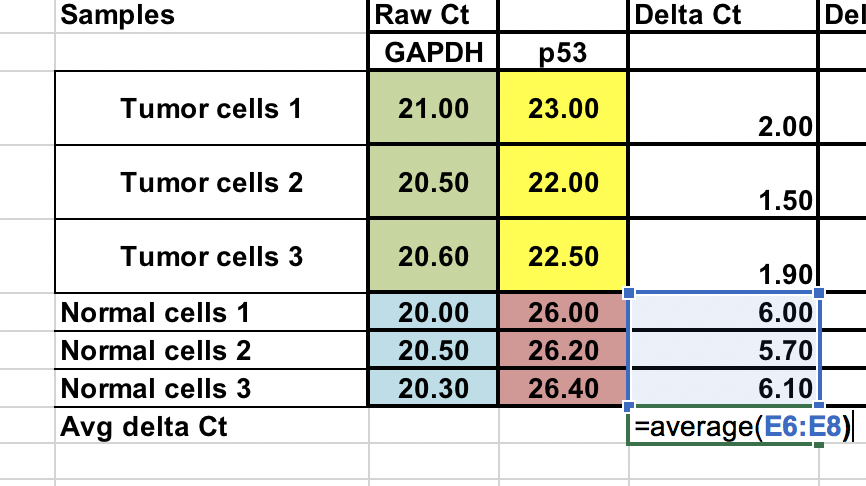
Media dei campioni di controllo (cellule normali)¶
Per confrontare il nostro tumore (trattamento) al controllo (cellule normali), prima dobbiamo fare la media del ∆Ct per i 3 campioni di controllo (normali).
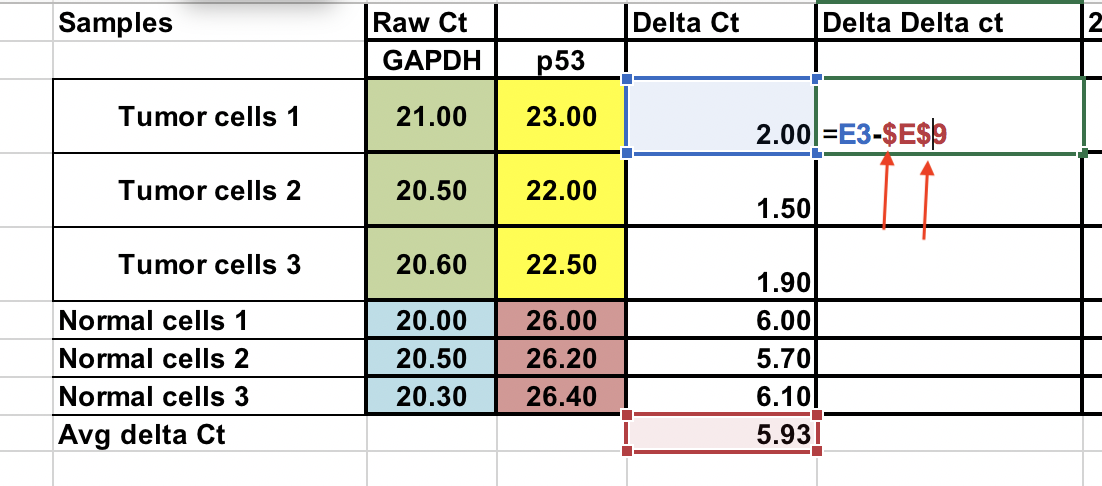
Calcolare il ∆∆Ct rispetto alla media del ∆Ct delle cellule normali cellule¶
∆∆Ct = ∆Ct (campione tumorale) – ∆Ct (media normale)
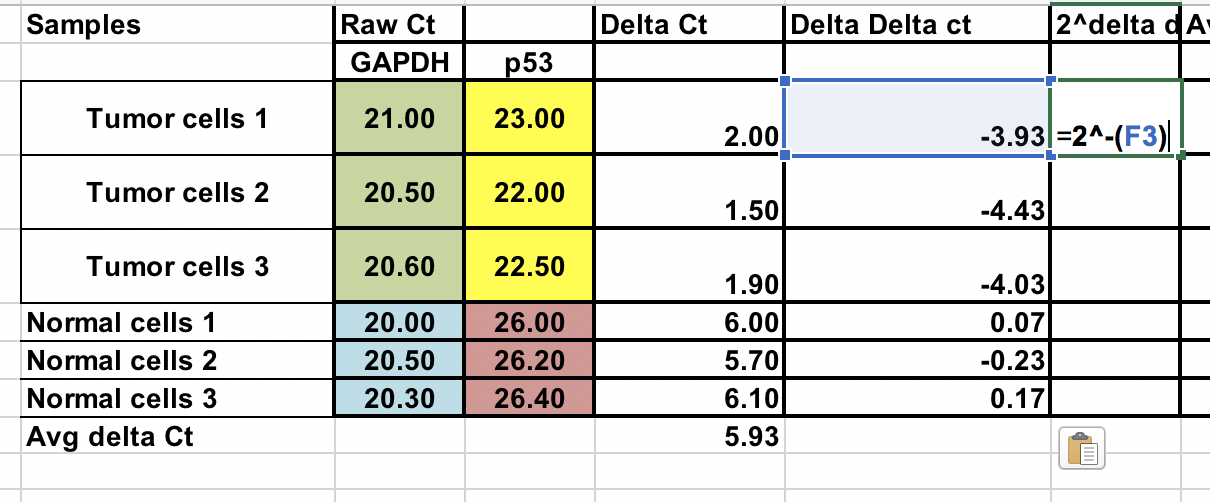
Puoi fare anche questo campione normale. Usate i segni $ davanti al numero della colonna e la lettera grezza (frecce) per fissare la cella.
Fold gene expression per ogni campione¶
Assicuratevi di aumentare il ∆∆Ct negativo alla potenza di due.
Fold gene expression = 2^-(∆∆Ct)
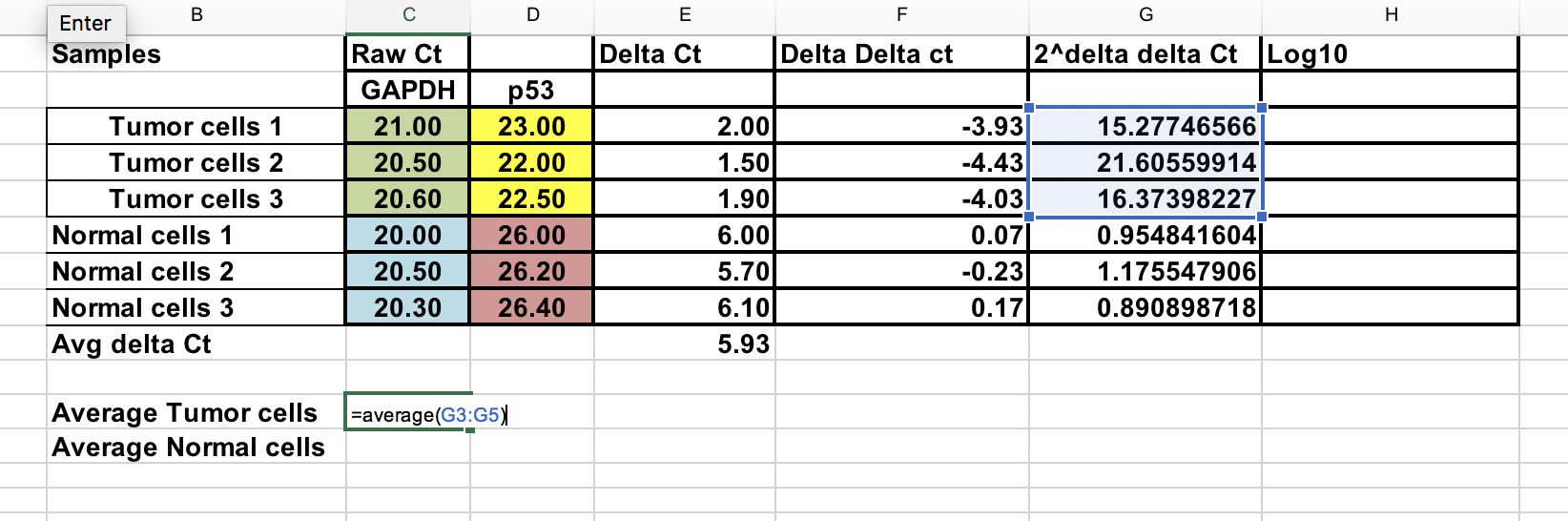
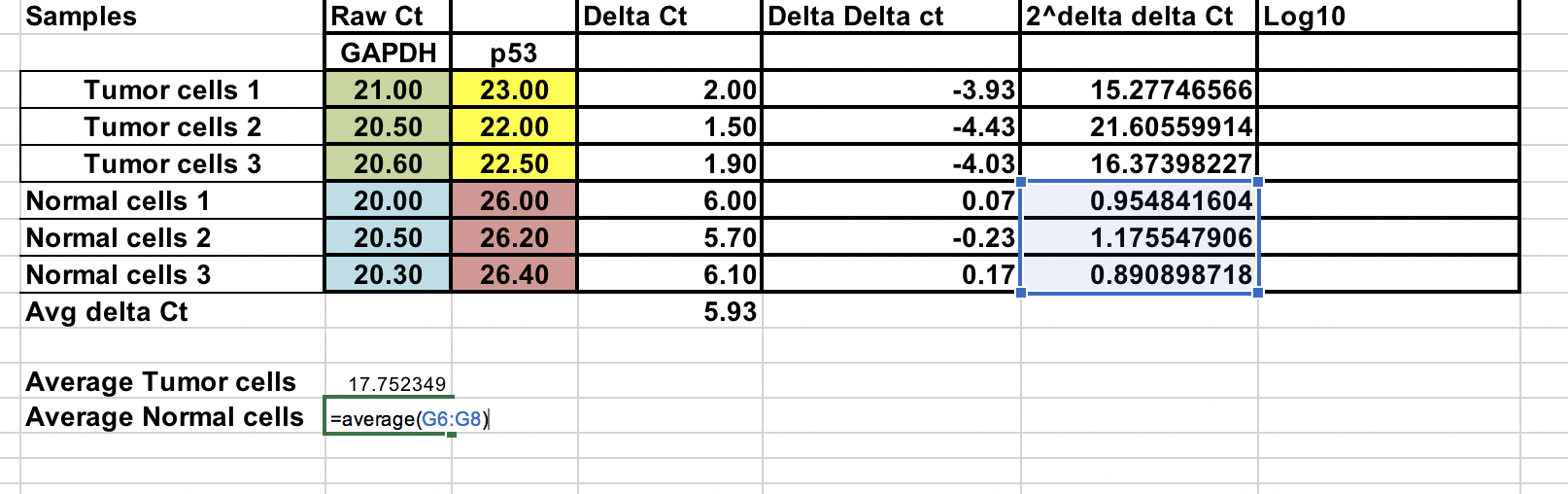
Overall fold change¶
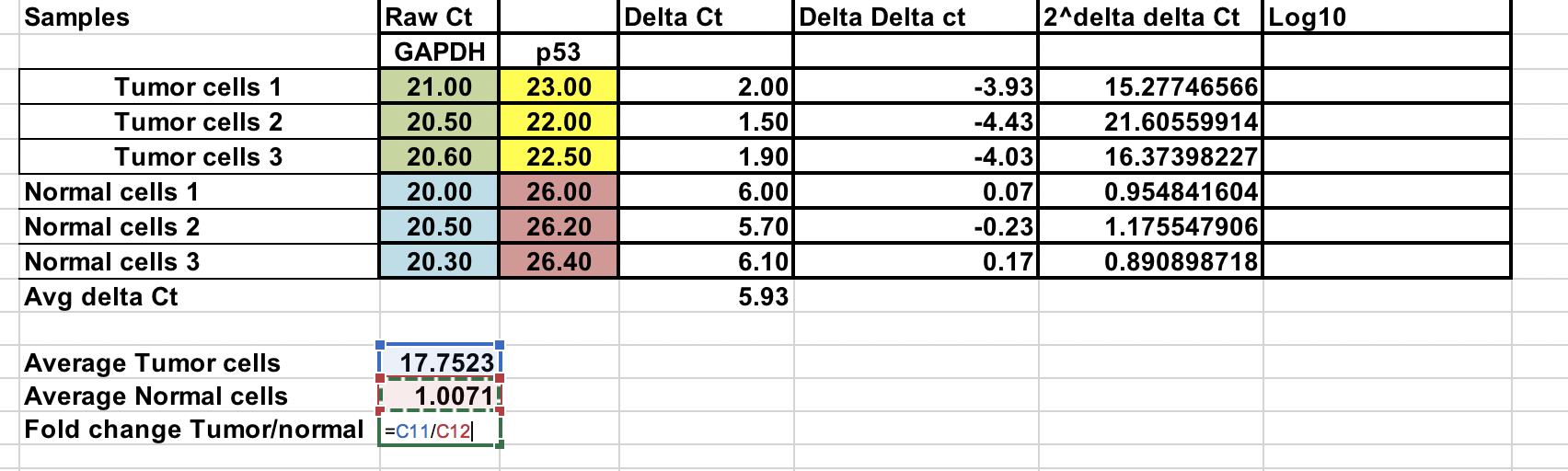
Puoi calcolare il fold change medio per entrambi i campioni tumorali e normali. Il rapporto tra questi due è il fold change tra campioni tumorali e normali.
Trasformazione log¶
Per eseguire test statistici parametrici come il test T, si consiglia di trasformare i risultati finali di espressione genica in valori log (qualsiasi base log). Questo renderebbe la distribuzione dei dati simmetrica.
Qui abbiamo cambiato il 2^-(∆∆Ct) in log 10.
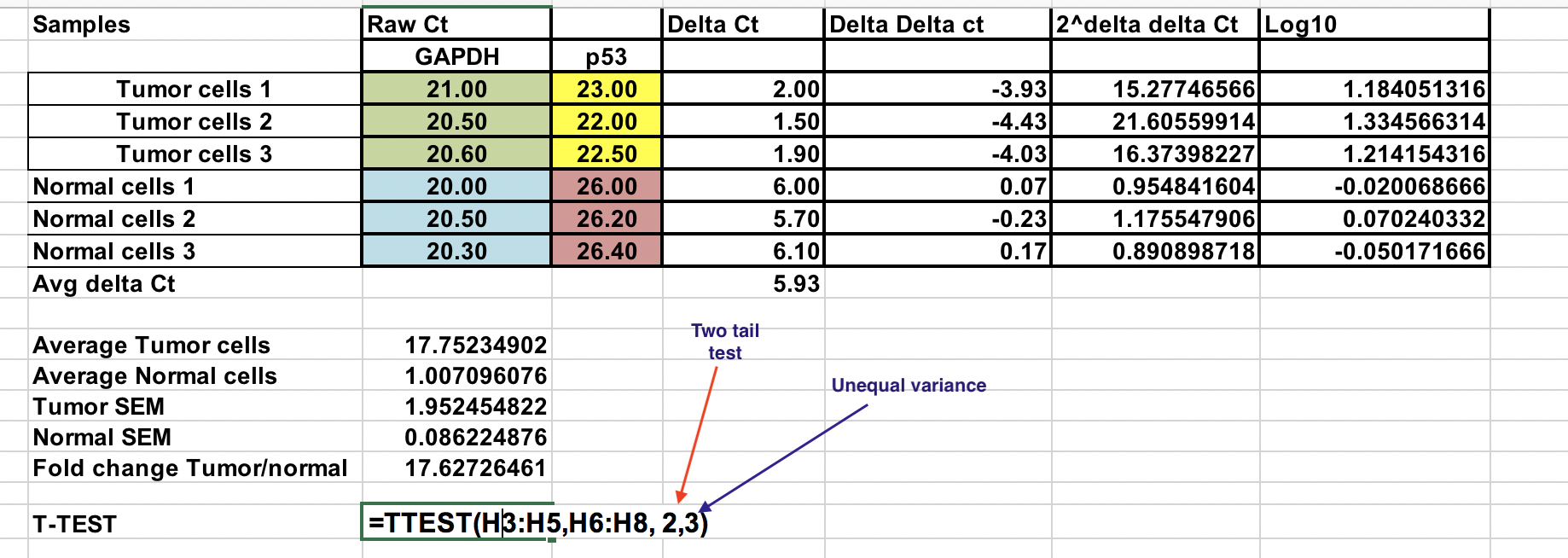
T-test¶
Necessario fare attenzione quando si usano test parametrici se i dati non sono normalmente distribuiti, porterebbe a conclusioni errate.
Selezionare il log 10 dei valori 2^-(∆∆Ct) per campioni normali e tumorali come indicato. Usare il test a due code (numero 2) e assumere varianza ineguale (3).
Il valore P risultante è inferiore a 0,05 e quindi, rifiutiamo l’ipotesi nulla e le medie dei due campioni sono significativamente diverse a livello 0,05.