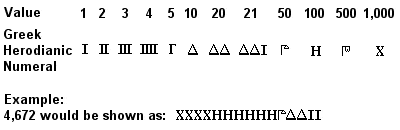
Numeri greci erodiani antichi
Quando l’impero greco cominciò a diffondere la sua sfera di influenza in Asia Minore, Mesopotamia e oltre, i greci erano abbastanza intelligenti da adottare e adattare elementi utili dalle società che avevano conquistato. Questo era vero per la loro matematica come per qualsiasi altra cosa, e adottarono elementi di matematica sia dai babilonesi che dagli egiziani. Ma presto iniziarono a dare importanti contributi per conto proprio e, per la prima volta, possiamo riconoscere i contributi degli individui. Nel periodo ellenistico, i greci avevano presieduto a una delle più drammatiche e importanti rivoluzioni nel pensiero matematico di tutti i tempi.
Numeri attici o erodiani
L’antico sistema numerico greco, noto come numeri attici o erodiani, fu completamente sviluppato intorno al 450 a.C., e in uso regolarmente forse già nel VII secolo a.C. Era un sistema a base 10 simile al precedente sistema egizio (e ancora più simile al successivo sistema romano), con simboli per 1, 5, 10, 50, 100, 500 e 1.000 ripetuti tante volte quanto necessario per rappresentare il numero desiderato. L’addizione si faceva totalizzando separatamente i simboli (1s, 10s, 100s, etc) nei numeri da aggiungere, e la moltiplicazione era un processo laborioso basato su raddoppi successivi (la divisione era basata sull’inverso di questo processo).
Teorema dell’intercetta di Talete
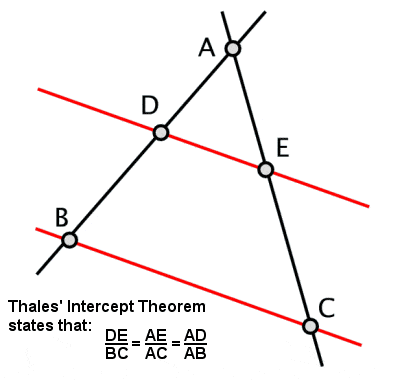
Teorema dell’intercetta di Talete
Ma la maggior parte della matematica greca era basata sulla geometria. Talete, uno dei Sette Saggi dell’Antica Grecia, che visse sulla costa ionica dell’Asia Minore nella prima metà del VI secolo a.C., è solitamente considerato il primo a stabilire le linee guida per lo sviluppo astratto della geometria, anche se ciò che sappiamo del suo lavoro (come sui triangoli simili e retti) sembra ora piuttosto elementare.
Tales stabilì quello che è diventato noto come Teorema di Talete, per cui se un triangolo è disegnato all’interno di un cerchio con il lato lungo come diametro del cerchio, allora l’angolo opposto sarà sempre un angolo retto (così come alcune altre proprietà correlate derivate da questo). Gli si attribuisce anche un altro teorema, noto anche come Teorema di Talete o Teorema dell’intercetta, sui rapporti dei segmenti di linea che si creano se due linee intersecanti sono intercettate da una coppia di parallele (e, per estensione, i rapporti dei lati di triangoli simili).
In qualche misura, tuttavia, la leggenda del matematico Pitagora di Samo del VI secolo a.C. è diventata sinonimo della nascita della matematica greca. Infatti, si ritiene che abbia coniato entrambe le parole “filosofia” (“amore per la saggezza”) e “matematica” (“ciò che si impara”). Pitagora fu forse il primo a capire che si poteva costruire un sistema matematico completo, in cui gli elementi geometrici corrispondevano ai numeri. Il Teorema di Pitagora (o il Teorema di Pitagora) è uno dei teoremi matematici più conosciuti. Ma rimane una figura controversa, come vedremo, e la matematica greca non era affatto limitata a un solo uomo.
Tre problemi geometrici
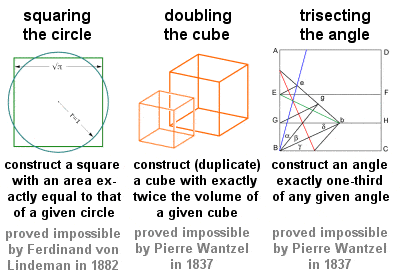
I tre problemi classici
Tre problemi geometrici in particolare, spesso indicati come i tre problemi classici, e tutti da risolvere con mezzi puramente geometrici usando solo una riga e un compasso, risalgono ai primi giorni della geometria greca: “la quadratura (o quadratura) del cerchio”, “il raddoppio (o duplicazione) del cubo” e “la trisezione di un angolo”. Questi problemi intransigenti influenzarono profondamente la geometria futura e portarono a molte scoperte fruttuose, anche se le loro soluzioni effettive (o, come risultò, le prove della loro impossibilità) dovettero aspettare fino al XIX secolo.
Hippocrates di Chios (da non confondere con il grande medico greco Ippocrate di Kos. Una biografia dettagliata qui.) fu uno dei matematici greci che si applicò a questi problemi durante il V secolo a.C. (il suo contributo al problema della “quadratura del cerchio” è noto come la Lune di Ippocrate). Il suo influente libro “Gli elementi”, risalente al 440 a.C. circa, fu la prima compilazione degli elementi della geometria, e il suo lavoro fu una fonte importante per il successivo lavoro di Euclide.
Il paradosso di Achille e la tartaruga di Zenone
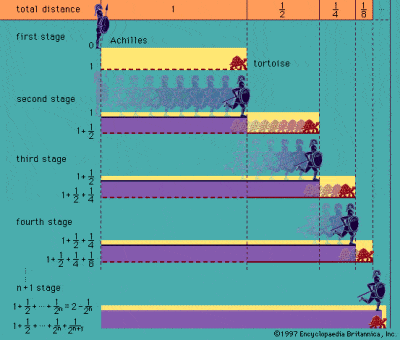
Il paradosso di Achille e la tartaruga di Zenone
Sono stati i greci i primi a confrontarsi con l’idea di infinito, come descritto nei noti paradossi attribuiti al filosofo Zenone di Elea nel V secolo a.C. Il più famoso dei suoi paradossi è quello di Achille e la tartaruga, che descrive una gara teorica tra Achille e una tartaruga. Achille dà alla tartaruga, molto più lenta, un vantaggio, ma quando Achille raggiunge il punto di partenza della tartaruga, quest’ultima è già andata avanti. Nel momento in cui Achille raggiunge quel punto, la tartaruga è andata avanti di nuovo, ecc, ecc, così che in linea di principio il veloce Achille non può mai raggiungere la tartaruga lenta.
Paradossi come questo e il cosiddetto paradosso della dicotomia di Zenone sono basati sulla divisibilità infinita dello spazio e del tempo, e si basano sull’idea che una metà più un quarto più un ottavo più un sedicesimo, ecc, ecc, all’infinito non sarà mai uguale a un intero. Il paradosso deriva, tuttavia, dal falso presupposto che è impossibile completare un numero infinito di trattini discreti in un tempo finito, anche se è estremamente difficile dimostrare definitivamente la fallacia. L’antico greco Aristotele fu il primo di molti a cercare di confutare i paradossi, soprattutto perché era un convinto sostenitore che l’infinito potesse essere solo potenziale e non reale.
Democrito, più famoso per le sue idee preveggenti sul fatto che tutta la materia fosse composta da minuscoli atomi, fu anche un pioniere della matematica e della geometria nel V – IV secolo a.C., e produsse opere con titoli come “Sui numeri”, “Sulla geometria”, “Sulle tangenze”, “Sulla mappatura” e “Sugli irrazionali”, anche se queste opere non sono sopravvissute. Sappiamo che fu tra i primi ad osservare che un cono (o piramide) ha un terzo del volume di un cilindro (o prisma) con la stessa base e altezza, ed è forse il primo ad aver seriamente considerato la divisione degli oggetti in un numero infinito di sezioni.
Tuttavia, è certamente vero che Pitagora in particolare influenzò molto coloro che vennero dopo di lui, compreso Platone, che fondò la sua famosa Accademia ad Atene nel 387 a.C., e il suo protetto Aristotele, la cui opera sulla logica fu considerata definitiva per oltre duemila anni. Il matematico Platone è meglio conosciuto per la sua descrizione dei cinque solidi platonici, ma il valore del suo lavoro come insegnante e divulgatore della matematica non può essere sopravvalutato.
Lo studente di Platone, Eudosso di Cnido, è solitamente accreditato con la prima implementazione del “metodo di esaurimento” (poi sviluppato da Archimede), un primo metodo di integrazione per approssimazioni successive che ha usato per il calcolo del volume della piramide e del cono. Sviluppò anche una teoria generale della proporzione, che era applicabile a grandezze incommensurabili (irrazionali) che non possono essere espresse come rapporto di due numeri interi, così come a grandezze commensurabili (razionali), estendendo così le idee incomplete di Pitagora.
Forse il più importante contributo singolo dei greci, però – e Pitagora, Platone e Aristotele furono tutti influenti in questo senso – fu l’idea della prova, e il metodo deduttivo di usare passi logici per dimostrare o confutare teoremi a partire da assiomi iniziali. Le culture più antiche, come gli egiziani e i babilonesi, si erano basate sul ragionamento induttivo, cioè usando osservazioni ripetute per stabilire regole empiriche. È questo concetto di prova che dà alla matematica il suo potere e garantisce che le teorie dimostrate siano vere oggi come lo erano duemila anni fa, e che ha posto le basi per l’approccio sistematico alla matematica di Euclide e di coloro che sono venuti dopo di lui.
| << Indietro alla matematica egizia | Avanti a Pitagora >> |