I diagrammi a blocchi consistono in un singolo blocco o una combinazione di blocchi. Sono usati per rappresentare i sistemi di controllo in forma pittorica.
Elementi di base del diagramma a blocchi
Gli elementi di base di un diagramma a blocchi sono un blocco, il punto di somma e il punto di stacco. Consideriamo il diagramma a blocchi di un sistema di controllo ad anello chiuso come mostrato nella figura seguente per identificare questi elementi.
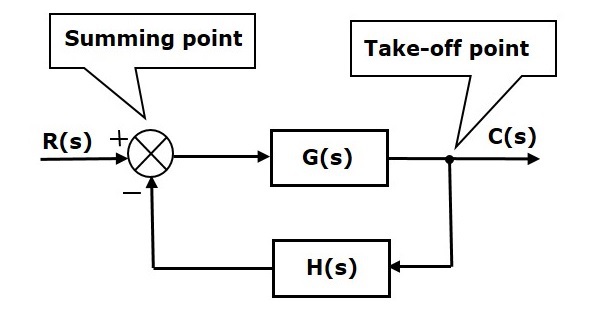
Il diagramma a blocchi di cui sopra consiste di due blocchi con funzioni di trasferimento G(s) e H(s). Ha anche un punto di somma e un punto di stacco. Le frecce indicano la direzione del flusso dei segnali. Discutiamo ora questi elementi uno per uno.
Blocco
La funzione di trasferimento di un componente è rappresentata da un blocco. Il blocco ha un singolo ingresso e una singola uscita.
La figura seguente mostra un blocco con ingresso X(s), uscita Y(s) e la funzione di trasferimento G(s).

Funzione di Trasferimento,$G(s)=\frac{Y(s)}{X(s)}$
$$$$$Freccia destra Y(s)=G(s)X(s)$$
L’uscita del blocco si ottiene moltiplicando la funzione di trasferimento del blocco per l’ingresso.
Punto di somma
Il punto di somma è rappresentato da un cerchio con una croce (X) al suo interno. Ha due o più ingressi e una sola uscita. Produce la somma algebrica degli ingressi. Esegue anche la somma o la sottrazione o la combinazione di somma e sottrazione degli ingressi in base alla polarità degli ingressi. Vediamo queste tre operazioni una per una.
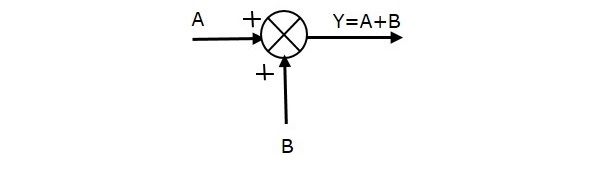
La figura seguente mostra il punto di somma con due ingressi (A, B) e un’uscita (Y). Qui, gli ingressi A e B hanno un segno positivo. Quindi, il punto di sommatoria produce l’uscita Y come somma di A e B.
i.e., Y = A + B.
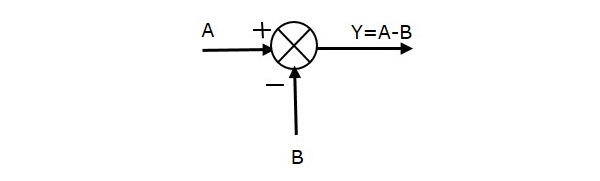
La figura seguente mostra il punto di sommatoria con due ingressi (A, B) e un’uscita (Y). Qui, gli ingressi A e B hanno segni opposti, cioè, A ha segno positivo e B ha segno negativo. Quindi, il punto di somma produce l’uscita Y come differenza di A e B.
Y = A + (-B) = A – B.
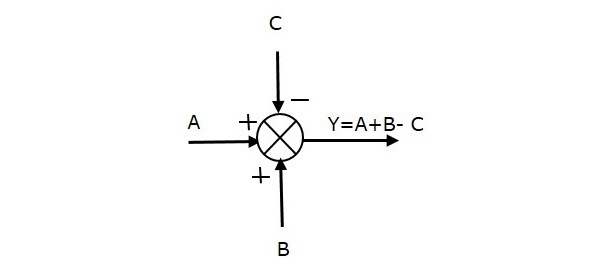
La figura seguente mostra il punto di somma con tre ingressi (A, B, C) e un’uscita (Y). Qui, gli ingressi A e B hanno segno positivo e C ha segno negativo. Quindi, il punto di sommatoria produce l’uscita Y come
Y = A + B + (-C) = A + B – C.
Punto di stacco
Il punto di stacco è un punto dal quale lo stesso segnale di ingresso può essere fatto passare attraverso più di un ramo. Ciò significa che con l’aiuto del punto di stacco, possiamo applicare lo stesso ingresso a uno o più blocchi, sommando i punti.
Nella figura seguente, il punto di stacco è usato per collegare lo stesso ingresso, R(s) a due più blocchi.
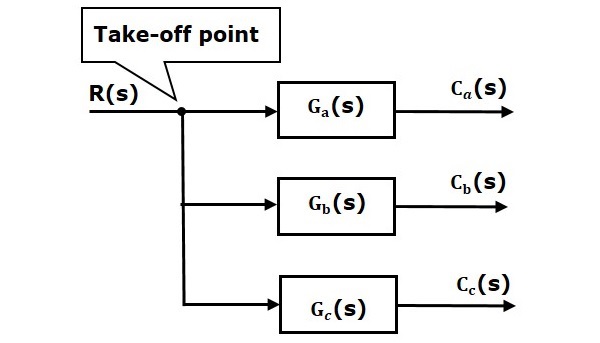
Nella figura seguente, il punto di stacco è usato per collegare l’uscita C(s), come uno degli ingressi al punto di somma.
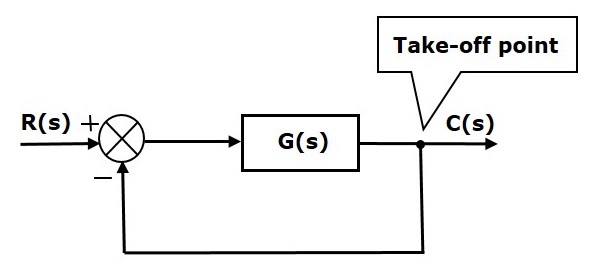
Rappresentazione del diagramma a blocchi dei sistemi elettrici
In questa sezione, rappresentiamo un sistema elettrico con un diagramma a blocchi. I sistemi elettrici contengono principalmente tre elementi di base – resistenza, induttore e condensatore.
Consideriamo una serie di circuito RLC come mostrato nella figura seguente. Dove Vi(t) e Vo(t) sono le tensioni di ingresso e di uscita. Sia i(t) la corrente che attraversa il circuito. Questo circuito è nel dominio del tempo.
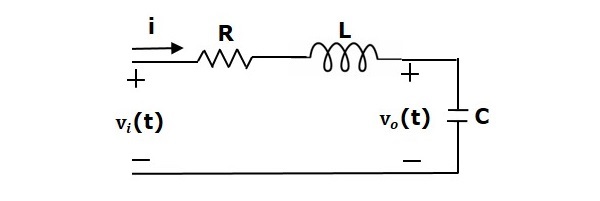
Applicando la trasformata di Laplace a questo circuito, si ottiene il circuito nel dominio s. Il circuito è come mostrato nella figura seguente.
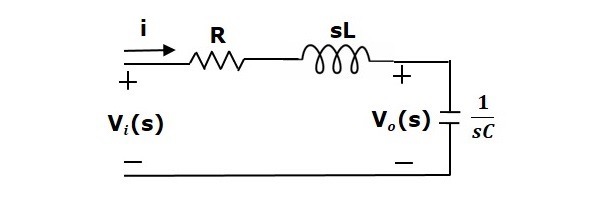
Dal circuito di cui sopra, possiamo scrivere
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$
$Freccia destra I(s)= \sinistra \frac{1}{R+sL} \(Equazione 1)
$$V_o(s)=\sinistra ( \frac{1}{sC} \destra )I(s)$ (Equazione 2)
Diamo ora i diagrammi a blocchi per queste due equazioni individualmente. E poi combiniamo questi schemi a blocchi correttamente per ottenere lo schema a blocchi complessivo della serie del circuito RLC (dominio s).
L’equazione 1 può essere implementata con un blocco che ha la funzione di trasferimento, $\frac{1}{R+sL}$. L’ingresso e l’uscita di questo blocco sono $sinistra \V_i(s)-V_o(s) \destra \}$ e $I(s)$. Abbiamo bisogno di un punto di somma per ottenere $sinistra \V_i(s)-V_o(s) \destra \}$. Lo schema a blocchi dell’equazione 1 è mostrato nella figura seguente.
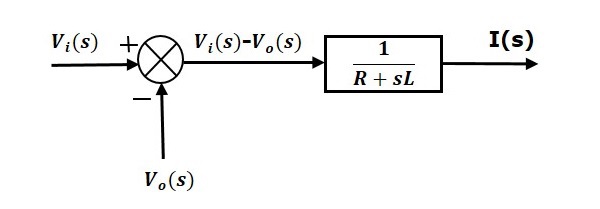
L’equazione 2 può essere implementata con un blocco con funzione di trasferimento, $frac{1}{sC}$. L’ingresso e l’uscita di questo blocco sono $I(s)$ e $V_o(s)$. Il diagramma a blocchi dell’equazione 2 è mostrato nella figura seguente.
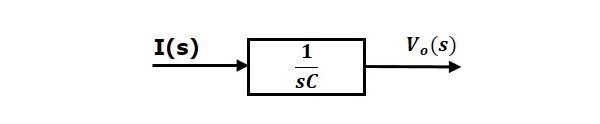
Il diagramma a blocchi complessivo della serie di circuiti RLC (dominio s) è mostrato nella figura seguente.
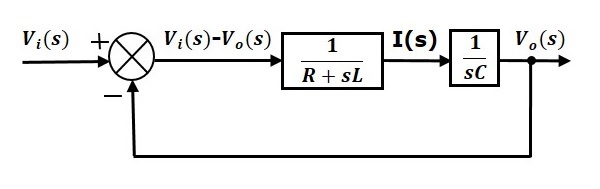
Similmente, puoi disegnare il diagramma a blocchi di qualsiasi circuito o sistema elettrico seguendo questa semplice procedura.
-
Converti il circuito elettrico nel dominio del tempo in un circuito elettrico nel dominio s applicando la trasformata di Laplace.
-
Scrivi le equazioni per la corrente che passa attraverso tutti gli elementi del ramo serie e la tensione attraverso tutti i rami shunt.
-
Scrivi i diagrammi a blocchi per tutte le equazioni di cui sopra individualmente.
-
Combina correttamente tutti questi schemi a blocchi per ottenere lo schema a blocchi complessivo del circuito elettrico (dominio s).