Strategie miste

Obiettivo di apprendimento

1. Quali giochi richiedono o ammettono la casualità come parte della loro soluzione?13 “Matching pennies again”.

   Figura 16.13 Matching pennies again

   

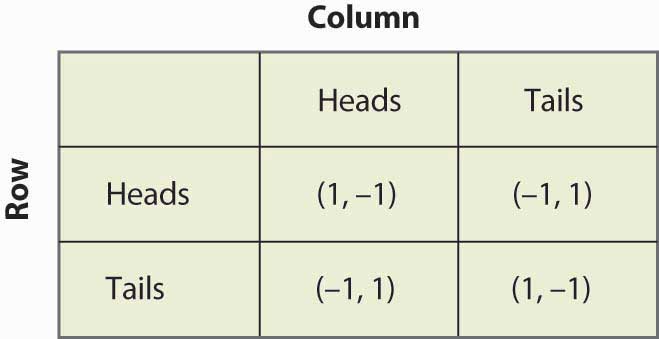
   Supponiamo che Row creda che Column giochi Heads con probabilità p. Allora se Row gioca Heads, Row ottiene 1 con probabilità p e -1 con probabilità (1 – p), per un valore atteso di 2p – 1. Allo stesso modo, se la fila gioca Croce, la fila ottiene -1 con probabilità p (quando la colonna gioca Testa), e 1 con probabilità (1 – p), per un valore atteso di 1 – 2p. Questo è riassunto nella Figura 16.14 “Strategia mista nell’accoppiamento dei penny”.

   Se 2p – 1 > 1 – 2p, allora a Row conviene, in media, giocare Testa che Croce. Allo stesso modo, se 2p – 1 < 1 – 2p, allora Row si trova meglio a giocare Croce che Testa. Se, d’altra parte, 2p – 1 = 1 – 2p, allora Row ottiene lo stesso payoff indipendentemente da ciò che fa Row. In questo caso, Row potrebbe giocare Testa, potrebbe giocare Croce, o potrebbe lanciare una moneta e randomizzare il gioco di Row.

   Un equilibrio di Nash a strategia mistaUn equilibrio di Nash in cui almeno un giocatore gioca una strategia randomizzata e nessun giocatore è in grado di aumentare il suo payoff atteso giocando una strategia alternativa. Un equilibrio di Nash in cui nessun giocatore randomizza è chiamato un equilibrio di Nash a strategia pura Un equilibrio di Nash in cui nessun giocatore randomizza..

   Figura 16.14 Strategia mista nel gioco dei penny

   

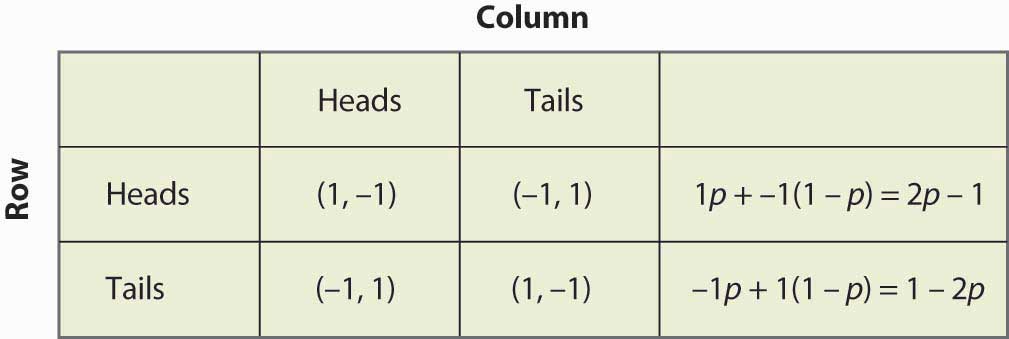
   Nota che la randomizzazione richiede l’uguaglianza dei payoff attesi. Se un giocatore deve randomizzare sulla strategia A o sulla strategia B, allora entrambe queste strategie devono produrre lo stesso payoff atteso. Altrimenti, il giocatore preferirebbe una delle due e non giocherebbe l’altra.

   Il calcolo di una strategia mista ha un elemento che spesso appare confuso. Supponiamo che Row stia per randomizzare. Allora i payoff di Row devono essere uguali per tutte le strategie che Row gioca con probabilità positiva. Ma questa uguaglianza nei payoffs di Row non determina le probabilità con cui Row gioca le varie file. Invece, quell’uguaglianza nei payoff della fila determinerà le probabilità con cui la colonna gioca le varie colonne. La ragione è che sono le probabilità della colonna a determinare i payoff attesi per la riga; se la riga sta per randomizzare, allora le probabilità della colonna devono essere tali che la riga è disposta a randomizzare.

   Così, per esempio, abbiamo calcolato il payoff per la riga di giocare Testa, che era 2p – 1, dove p era la probabilità che la colonna giocasse Testa. Allo stesso modo, il payoff per la fila di giocare Croce era 1 – 2p. La fila è disposta a randomizzare se questi sono uguali, il che risolve per p = ½.

   Ora proviamo un esempio un po’ più impegnativo e rivisitiamo la battaglia dei sessi. La figura 16.15 “Strategia mista nella battaglia dei sessi” illustra i payoff ancora una volta.

   Figura 16.15 Strategia mista nella battaglia dei sessi

   

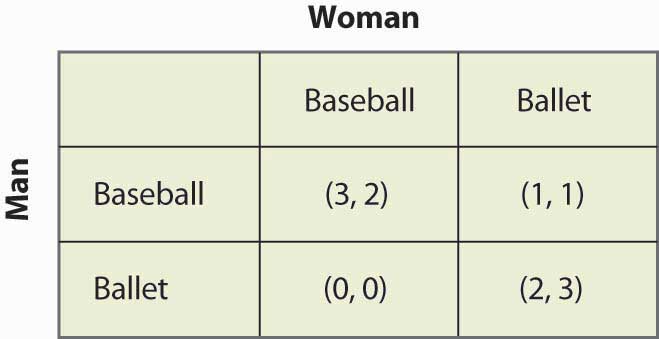
   Questo gioco ha due equilibri di Nash a strategia pura: (Baseball, Baseball) e (Ballet, Ballet). Esiste una strategia mista? Per calcolare una strategia mista, lasciamo che la Donna vada al gioco del Baseball con probabilità p, e l’Uomo vada al gioco del Baseball con probabilità q. La figura 16.16 “Calcolo completo della strategia mista” contiene il calcolo dei payoff della strategia mista per ogni giocatore.

   Figura 16.16 Calcolo completo della strategia mista

   

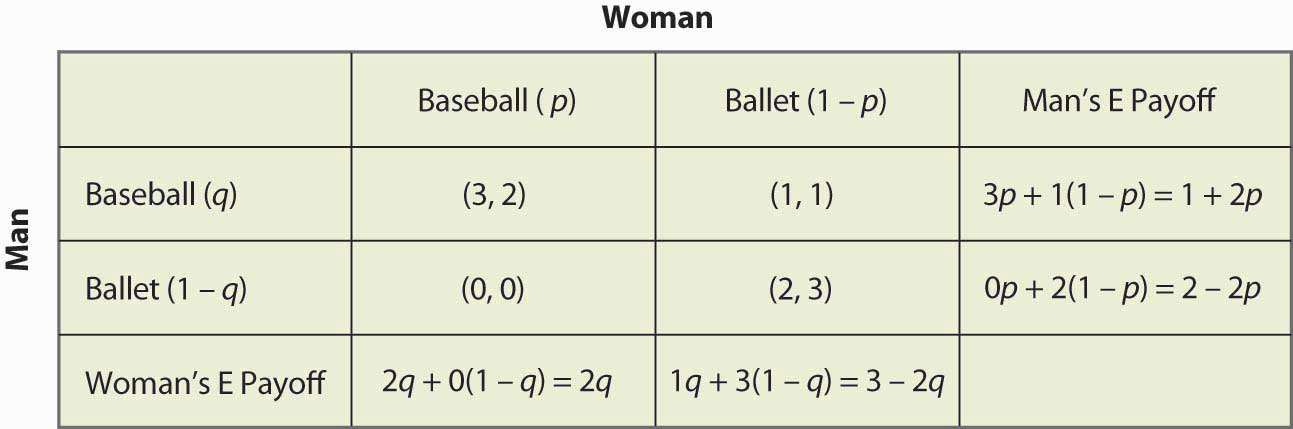
   Per esempio, se l’Uomo (giocatore di fila) va alla partita di Baseball, ottiene 3 quando la Donna va alla partita di Baseball (probabilità p), e altrimenti ottiene 1, per un payoff atteso di 3p + 1(1 – p) = 1 + 2p. Gli altri calcoli sono simili, ma si dovrebbe sicuramente eseguire la logica e verificare ogni calcolo.

   Una strategia mista nel gioco della battaglia dei sessi richiede che entrambe le parti randomizzino (poiché una strategia pura di una delle parti impedisce la randomizzazione dell’altra). L’indifferenza dell’uomo tra andare al gioco del baseball e al balletto richiede 1 + 2p = 2 – 2p, che produce p = ¼. Cioè, l’uomo sarà disposto a randomizzare quale evento frequentare se la donna andrà al balletto per ¾ del tempo, e altrimenti alla partita di baseball. Questo rende l’Uomo indifferente tra i due eventi perché preferisce stare con la Donna, ma gli piace anche essere alla partita di Baseball. Per compensare il vantaggio che il gioco gli offre, la Donna deve essere al Balletto più spesso.

   Similmente, perché la Donna randomizzi, la Donna deve ottenere payoff uguali andando alla partita di Baseball e andando al Balletto, il che richiede 2q = 3 – 2q, o q = ¾. Così, la probabilità che l’uomo vada alla partita di baseball è ¾, e va al balletto ¼ delle volte. Queste sono probabilità indipendenti, quindi per ottenere la probabilità che entrambi vadano alla partita di baseball, moltiplichiamo le probabilità, che dà come risultato 3/16. La figura 16.17 “Probabilità di strategia mista” compila le probabilità per tutti e quattro i possibili risultati.

   Figura 16.17 Probabilità di strategia mista

   

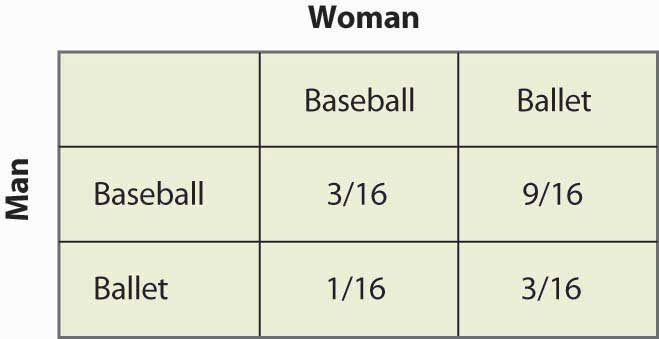
   Nota che più della metà delle volte (Baseball, Balletto) è il risultato della strategia mista e le due persone non sono insieme. Questa mancanza di coordinazione è generalmente una caratteristica degli equilibri a strategia mista. Anche i payoff attesi per entrambi i giocatori sono facilmente calcolabili. Il payoff dell’Uomo è 1 + 2p = 2 – 2p, e poiché p = ¼, l’Uomo ottiene 1½. Un calcolo simile mostra che il payoff della Donna è lo stesso. Quindi, entrambi fanno peggio che coordinarsi sul loro risultato meno preferito. Ma questo equilibrio di Nash a strategia mista, per quanto indesiderabile possa sembrare, è un equilibrio di Nash nel senso che nessuna delle due parti può migliorare il proprio payoff, dato il comportamento dell’altra parte.

   Nella battaglia dei sessi, l’equilibrio di Nash a strategia mista può sembrare improbabile; e ci potremmo aspettare che la coppia si coordini in modo più efficace. Infatti, una semplice chiamata al telefono dovrebbe escludere la strategia mista. Consideriamo quindi un altro gioco legato alla battaglia dei sessi, dove il fallimento della coordinazione ha più senso. Questo è il gioco del “pollo”. In questo gioco, due giocatori guidano l’uno verso l’altro, cercando di convincere l’altro a cedere e alla fine a sterzare in un fosso. Se entrambi sbandano nel fosso, chiameremo il risultato un pareggio ed entrambi avranno zero. Se uno sterza e l’altro no, il guidatore che sterza perde e l’altro vince, e daremo al vincitore un punto. Si noti che aggiungere una costante ai payoff di un giocatore, o moltiplicare i payoff di quel giocatore per una costante positiva, non influenza gli equilibri di Nash – puri o misti. Pertanto, possiamo sempre lasciare che un risultato per ogni giocatore sia zero, e un altro risultato sia uno. L’unica questione che rimane è cosa succede quando nessuno dei due cede, nel qual caso si verifica un crash. In questa versione, il payoff è stato fissato a quattro volte la perdita di sterzare, come mostrato nella figura 16.18 “Chicken”, ma è possibile cambiare il gioco e vedere cosa succede.

   Figura 16.18 Chicken

   

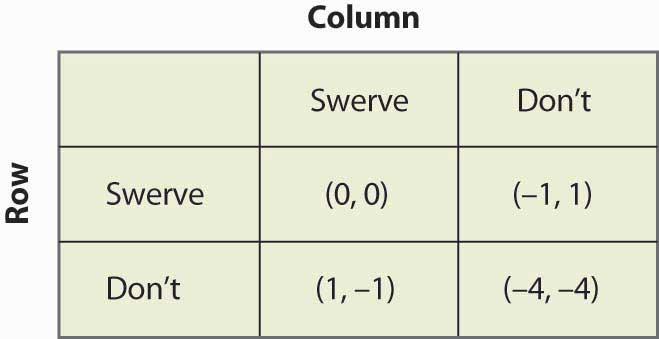
   Questo gioco ha due equilibri di strategia pura: (Swerve, Don’t) e (Don’t, Swerve). Inoltre, ha una strategia mista. Supponiamo che la colonna sterzi con probabilità p. Allora Row ottiene 0p + -1(1 – p) da sterzare, 1p + (-4)(1 – p) da non sterzare, e Row randomizzerà se questi sono uguali, il che richiede p = ¾. Cioè, la probabilità che la colonna sterzi in un equilibrio di strategia mista è ¾. Si può verificare che il giocatore di fila ha la stessa probabilità impostando la probabilità che la fila sterzi uguale a q e calcolando i payoff attesi della colonna. Così, la probabilità di una collisione è 1/16 nell’equilibrio a strategia mista.

   L’equilibrio a strategia mista è più probabile, in un certo senso, in questo gioco: Se i giocatori sapessero già chi cederà, non avrebbero bisogno di giocare il gioco. L’intero scopo del gioco è quello di scoprire chi cederà, il che significa che non è noto in anticipo. Questo significa che l’equilibrio a strategia mista è, in un certo senso, l’equilibrio più ragionevole.

   Figura 16.19 Sasso, carta, forbici

   

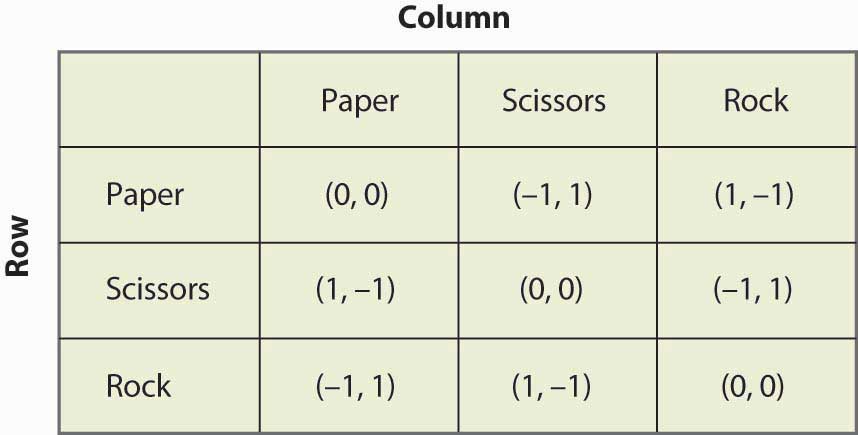
   “Sasso, carta, forbici” è un gioco per bambini in cui due bambini usano le loro mani per scegliere contemporaneamente carta (mano tenuta piatta), forbici (mano con due dita sporgenti per sembrare forbici) o sasso (mano in un pugno). La natura dei payoff è che la carta batte il sasso, il sasso batte le forbici e le forbici battono la carta. Questo gioco ha la struttura illustrata nella Figura 16.19 “Sasso, carta, forbici”.

   Punti chiave

   • Un equilibrio di Nash a strategia mista implica che almeno un giocatore giochi una strategia randomizzata e che nessun giocatore possa aumentare il suo payoff atteso giocando una strategia alternativa.
   • Un equilibrio di Nash senza randomizzazione è chiamato equilibrio di Nash a strategia pura.
   • Se si suppone che un giocatore possa randomizzare su due strategie, allora entrambe devono produrre lo stesso payoff atteso.
   • Il gioco dei penny abbinati ha una strategia mista e nessuna strategia pura.
   • Il gioco della battaglia dei sessi ha una strategia mista e due strategie pure.
   • Il gioco del pollo è simile alla battaglia dei sessi e, come esso, ha due strategie pure e una strategia mista.

   Esercizi

   1. Sia q la probabilità che la fila giochi Testa. Mostrare che Colonna è disposta a randomizzare, se e solo se q = ½. (Suggerimento: prima calcola il payoff atteso della colonna quando la colonna gioca Testa, e poi calcola il payoff atteso della colonna quando la colonna gioca Croce. Questi devono essere uguali perché la colonna si randomizzi.
   2. Mostra che nel gioco sasso, carta, forbici non ci sono equilibri di strategia pura. Mostra che giocare tutte e tre le azioni con uguale probabilità è un equilibrio di strategia mista.

   3. Trova tutti gli equilibri dei seguenti giochi:

      Figura 16.20

      

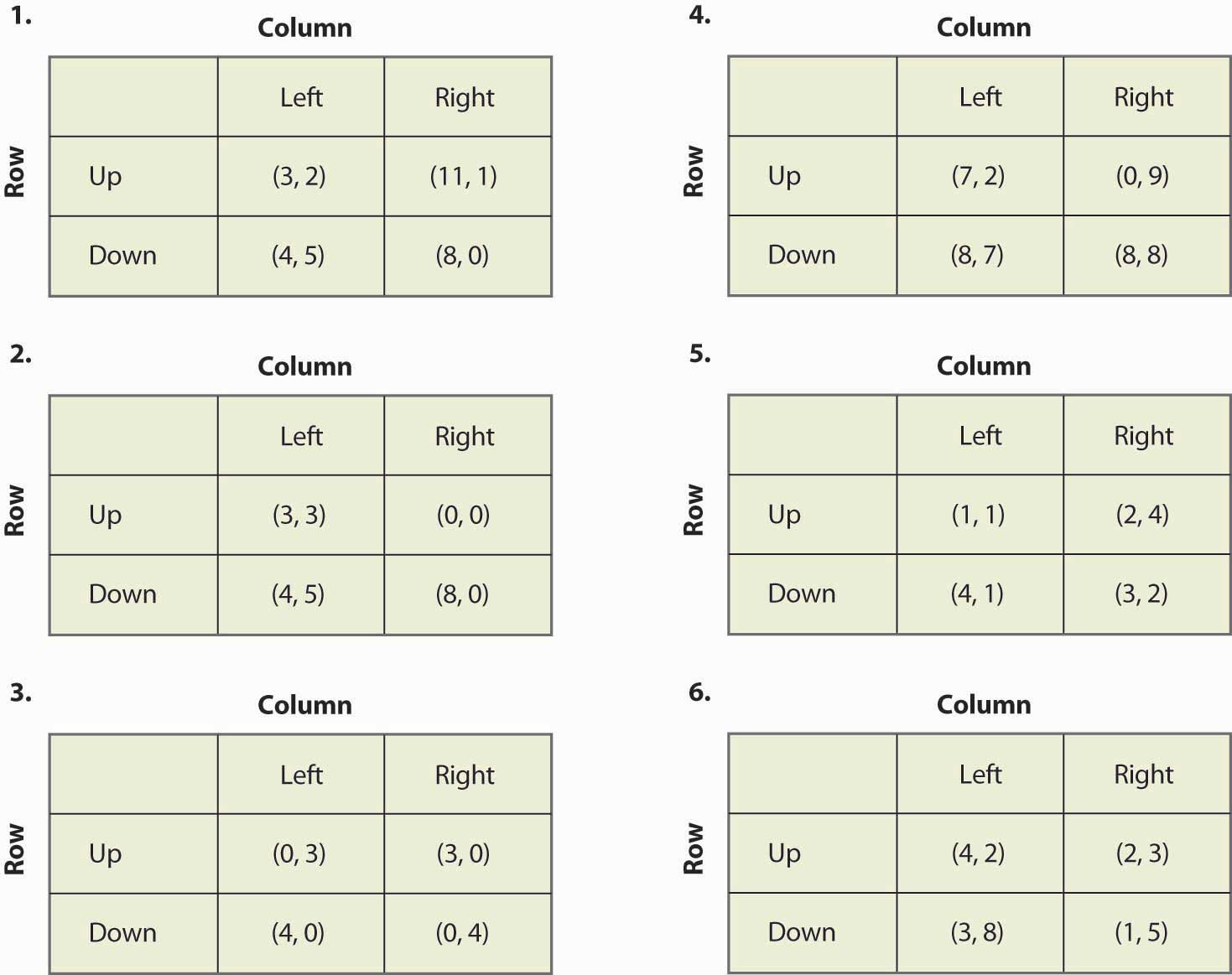
   4. Se si moltiplica il payoff di un giocatore per una costante positiva, gli equilibri del gioco non cambiano. È vero o falso, e perché?