Archimedische spiralen worden vaak gebruikt in de analyse van inductor spoelen, spiraal warmtewisselaars, en microfluïdische apparaten. Vandaag zullen we demonstreren hoe een Archimedespiraal kan worden gebouwd met behulp van analytische vergelijkingen en hun afgeleiden om een reeks spiraalkrommen te definiëren. Op basis van deze krommen zullen we dan een 2D geometrie met een specifieke dikte maken, en deze extruderen tot een volledige 3D geometrie.
Een korte inleiding tot Archimedespiralen
Wijdverbreid waargenomen in de natuur, worden spiralen, of helices, gebruikt in veel technische ontwerpen. Als elektrotechnisch ingenieur kun je bijvoorbeeld inductieve spoelen in spiraalpatronen wikkelen en spiraalvormige antennes ontwerpen. Als werktuigbouwkundig ingenieur kun je spiralen gebruiken bij het ontwerpen van veren, spiraalvormige tandwielen of zelfs het hieronder getoonde uurwerkmechanisme.

Een voorbeeld van een Archimedes-spiraal die in een uurwerkmechanisme wordt gebruikt. Afbeelding door Greubel Forsey. Gelicentieerd door CC BY-SA 3.0, via Wikimedia Commons.
Hier zullen we ons richten op een specifiek type spiraal, namelijk de spiraal die wordt gebruikt in het hierboven getoonde mechanisme: een Archimedespiraal. Een Archimedespiraal is een type spiraal met een vaste afstand tussen de opeenvolgende wendingen. Deze eigenschap maakt dat zij veel gebruikt wordt bij het ontwerpen van platte spoelen en veren.
We kunnen een Archimedes-spiraal beschrijven met de volgende vergelijking in poolcoördinaten:
waarbij a en b parameters zijn die de beginstraal van de spiraal bepalen en de afstand tussen de opeenvolgende windingen, waarvan de laatste gelijk is aan 2 \pi b. Merk op dat een Archimedes-spiraal ook wel eens een rekenkundige spiraal wordt genoemd. Deze naam is afgeleid van de rekenkundige progressie van de afstand van de oorsprong tot het punt op dezelfde radiaal.
Ontwerpen van een Geparameteriseerde Archimedische Spiraal Geometrie
Nu we Archimedische spiralen hebben geïntroduceerd, laten we eens kijken hoe we zo’n ontwerp kunnen parametriseren en creëren voor analyse in COMSOL Multiphysics.
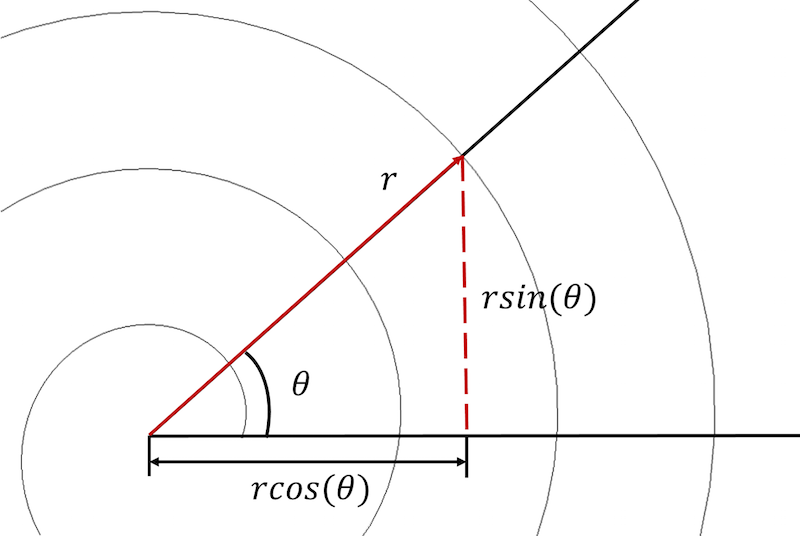
Een Archimedespiraal kan zowel in poolcoördinaten als in cartesiaanse coördinaten worden beschreven.
Om te beginnen moeten we de spiraalvergelijkingen omzetten van een poolcoördinatensysteem naar een cartesiaans coördinatensysteem en elke vergelijking uitdrukken in een parametrische vorm:
x_{component}=rcos(\theta) \
y_{component}=rsin(\theta)
eind{align*}
Met deze transformatie kunnen we de vergelijking van de Archimedische spiraal herschrijven in een parametrische vorm in het cartesische coördinatenstelsel:
x_{component}=(a+b_theta)cos(\theta) \
y_{component}=(a+b_theta)sin(\theta)
eind{align*}
In COMSOL Multiphysics, is het nodig om de set parameters te bepalen die de geometrie van de spiraal zal bepalen. Deze parameters zijn de beginstraal van de spiraal a_{initial}, de eindstraal van de spiraal a_{final}, en het gewenste aantal omwentelingen n. De groeisnelheid van de spiraal b kan dan worden uitgedrukt als:
Verder moeten we de beginhoek theta_0 en de eindhoek theta_f van de spiraal bepalen. Laten we beginnen met de waarden theta_0=0 en theta_f=2 \pi n. Met deze informatie kunnen we een set parameters definiëren voor de spiraal geometrie.
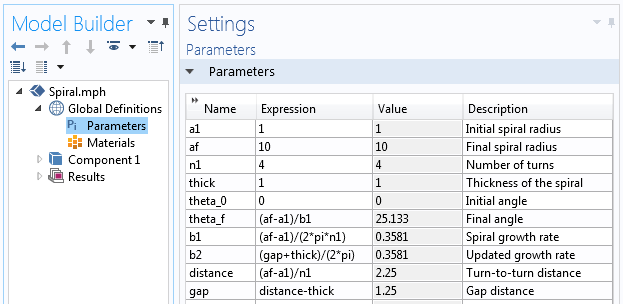
De parameters die worden gebruikt om de spiraal geometrie op te bouwen.
Om deze spiraal op te bouwen, beginnen we met een 3D Component en maken een Work Plane in de Geometrie tak. In de Work Plane geometrie voegen we vervolgens een Parametric Curve toe en gebruiken de hierboven genoemde parametrische vergelijkingen met een variërende hoek om een 2D versie van de Archimedes spiraal te tekenen. Deze vergelijkingen kunnen direct worden ingevoerd in het Uitdrukkingsveld van de parametrische kromme, of we kunnen eerst elke vergelijking in een nieuwe Analytische functie definiëren als:
X_{fun}=(a+bs)cos(s) \
Y_{fun}=(a+bs)sin(s) \
eind{align*}
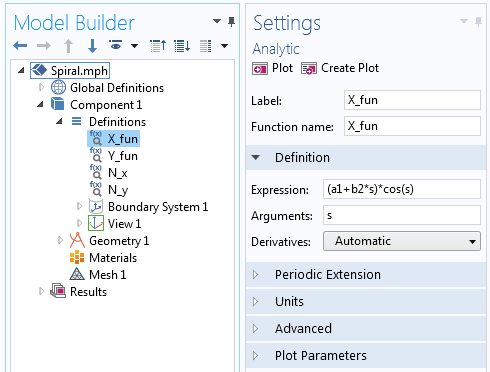
De X-component van de Archimedische spiraalvergelijking gedefinieerd in de Analytische functie.
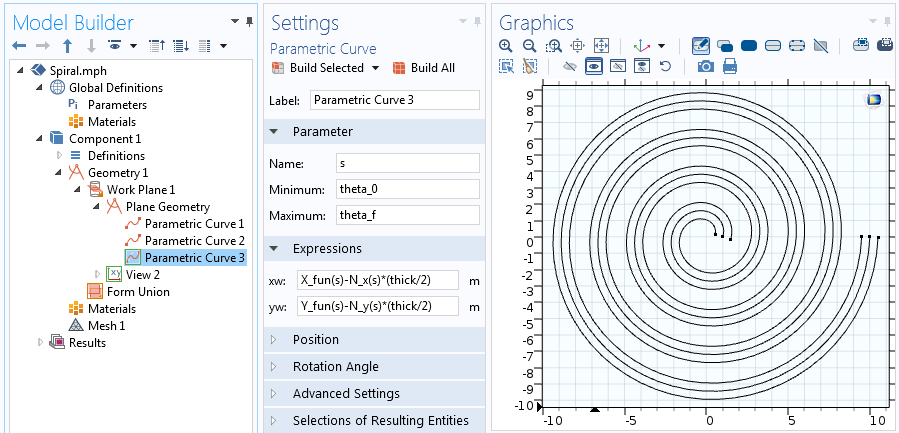
De Analytische functie kan worden gebruikt in de uitdrukkingen voor de Parametrische kromme. In deze Parametrische Kromme, variëren we parameter s van de beginhoek van de spiraal, theta_0, tot de eindhoek van de spiraal, theta_f=2 \pi n.
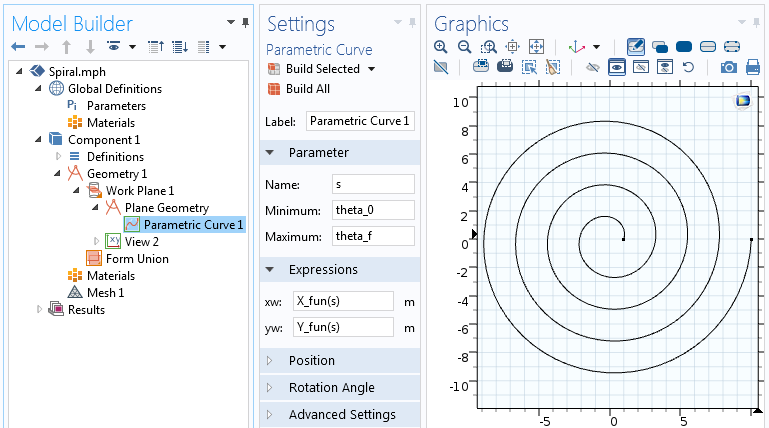
De instellingen voor de Parametrische Kromme functie.
De parametrische spiraal vergelijkingen gebruikt in de Parametrische Kromme functie zal resulteren in een spiraal voorgesteld door een kromme. Laten we nu voortbouwen op deze geometrie en er dikte aan toevoegen om een 2D massief object te maken.
Tot nu toe is onze spiraal geparametriseerd in termen van de beginstraal a_{initial}, eindstraal a_{final}, en het gewenste aantal omwentelingen n. Nu moeten we de dikte als een andere controleparameter in de spiraalvergelijking opnemen.
Laten we beginnen met de belangrijkste eigenschap van de spiraal, die stelt dat de afstand tussen de spiraalomwentelingen gelijk is aan 2 \pi b. Dit is ook gelijk aan \frac{a_{final}-a_{initial}}{n}. Om de dikte mee te nemen, stellen we de afstand tussen elke opeenvolgende draai van de spiraal voor als een som van de spiralendikte en de resterende spleet tussen de draaiingen, thick+gap.
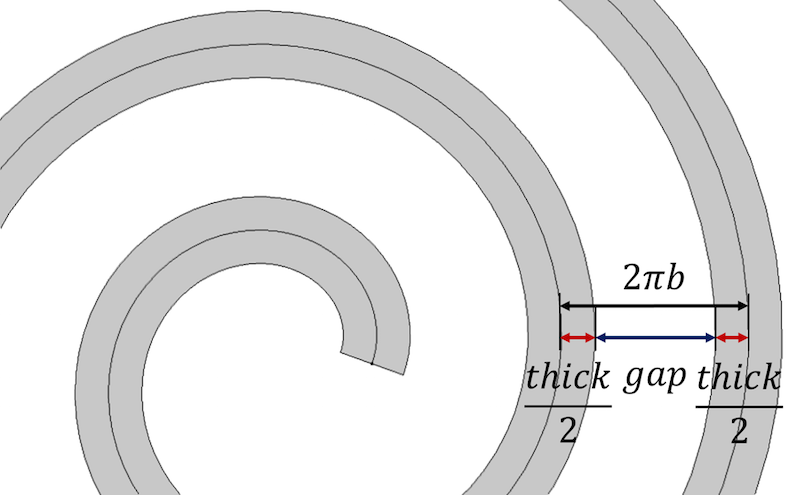
De afstand tussen spiralen draaiingen wordt gedefinieerd in termen van de parameters spiralendikte en spleet.
Om de dikte te regelen en een gelijke afstand tussen de windingen te verkrijgen, kan de afstand worden uitgedrukt als:
afstand=:frac{a_{initial}-a_{final}}{n}
afstand=afstand-dikte
einde{align*}
Na het definiëren van de dikte en het uitdrukken van de afstand tussen de wikkelingen in termen van dikte en constante afstand tussen de middellijnen van de spiraal, kunnen we de groeiparameter van de spiraal in termen van dikte herschrijven als:
afstand=2:pi b \5931>b={gap+thick}{2:pi}
:eind{align*}
We zullen ook de uiteindelijke hoek van de spiraal willen uitdrukken in termen van de begin- en eindstralen:
theta_{final}=2 \pi n \
a_{final}=:tekst{totale afstand}+a_{initial} \
a_{final}=2 \pi bn+a_{initial} \
n=\frac{a_{final}-a_{initial}}{2 \pi b} \
theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \
theta_{final}=\frac{a_{final}-a_{initial}}{b}
einde{align*}
Wilt u de spiraal vanuit een andere hoek dan nul laten beginnen? Zo ja, dan moet je deze beginhoek toevoegen aan je eindhoek in de uitdrukking voor de parameter: theta_f=\frac{a_{final}-a_{initial}{b}+theta_0.
Door de bestaande spiraalcurve tweemaal te dupliceren en deze curven met een offset van -\frac{thick}{2} en +\frac{thick}{2} te plaatsen ten opzichte van de beginspiraalcurve, kunnen we de spiraal met dikte opbouwen. Om de bovenste en onderste spiralen correct te plaatsen, moeten we ervoor zorgen dat de offset spiralen normaal liggen ten opzichte van de initiële spiraalkromme. Dit kan worden bereikt door de offset afstand \pm{dikte}{2} te vermenigvuldigen met de eenheidsvector normaal aan de spiraalkromme. De vergelijkingen van de normaalvectoren naar een kromme in parametrische vorm zijn:
waarbij s de parameter is die gebruikt wordt in de Parametrische kromme functie. Om een eenheidsnormaal te krijgen, moeten we deze uitdrukkingen delen door de lengte van de normaal:
Onze bijgewerkte parametrische vergelijkingen voor de Archimedes-spiraal met een halfdikteverschuiving zijn:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2}
y_{component}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2}
einde{align*}
Het uitschrijven van deze vergelijkingen in de uitdrukkingsvelden van de parametrische kromme kan nogal tijdrovend zijn. Daarom introduceren we de volgende notatie:
N_x=-(dx/ds)^2+(dy/ds)^2} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
waarbij elke N_x en N_y wordt gedefinieerd via de Analytische functie in COMSOL Multiphysics, vergelijkbaar met hoe we X_{fun} en Y_{fun} hebben gedefinieerd voor de eerste parametrische kromme. Binnen de functie gebruiken we de differentiatie-operator, d(f(x),x), om de afgeleide te nemen, zoals afgebeeld in de volgende schermafbeelding.
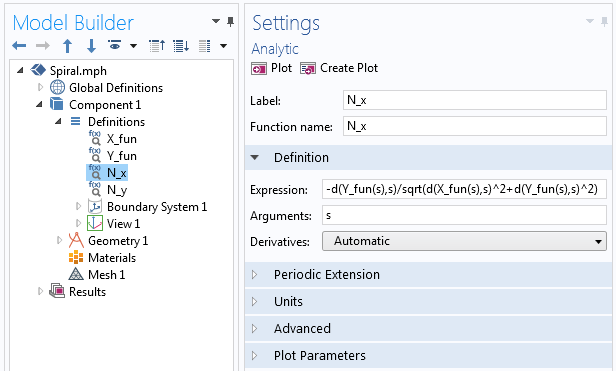
Voorbeelden van de afgeleide-operator die in de Analytische functie wordt gebruikt.
De functies X_{fun}, Y_{fun}, N_x, en N_y kunnen dan rechtstreeks worden gebruikt in de uitdrukkingen van de parametrische kromme voor de kromme aan één zijde:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
De functies kunnen ook gebruikt worden voor de kromme aan de andere kant:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2}
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
einde{align*}
Vergelijkingen voor de tweede van de twee offset parametrische krommen.
Om de uiteinden van twee krommen samen te voegen, voegen we nog twee parametrische krommen toe met behulp van een kleine wijziging van de hierboven genoemde vergelijkingen. Voor de kromme die het midden van de spiraal verbindt, moeten we X_{fun}, Y_{fun}, N_x, en N_y berekenen voor de beginwaarde van de hoek, theta. Voor de kromme die aan de buitenkant van de spiraal aansluit, moeten we de eindwaarde van theta bepalen. Daarom is de verbindingskromme in het centrum:
X_{fun}(theta_0)+s_cdot N_x(theta_0)\cdot \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
De buitenste verbindingskromme is dan:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
In beide bovenstaande vergelijkingen gaat s van -1 naar +1, zoals te zien is in de schermafbeelding hieronder.
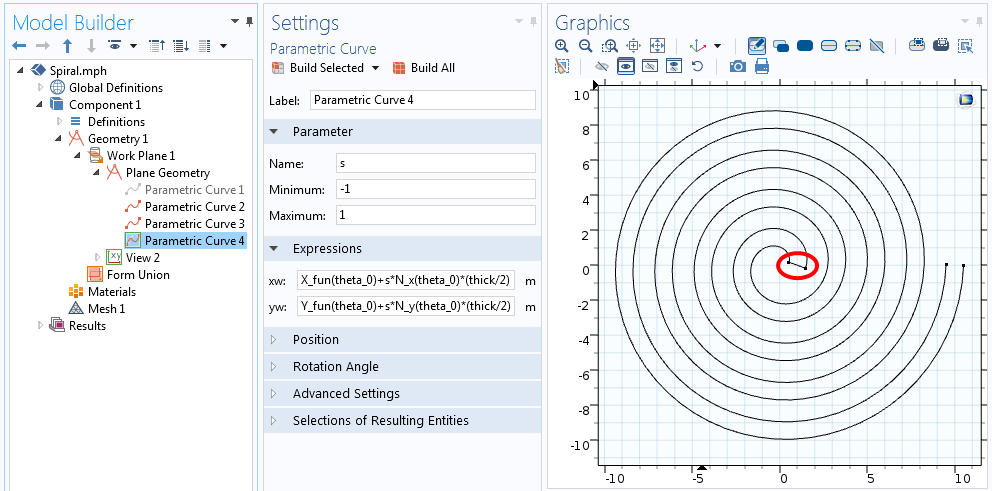
Vergelijkingen voor de kromme die één uiteinde van de spiraal verbindt.
We hebben nu vijf krommen die de middellijn van de spiraal en alle vier de zijden van het profiel bepalen. We kunnen de kromme die de middellijn beschrijft uitschakelen (of zelfs verwijderen) omdat die niet echt nodig is, zodat we alleen de omtrek van de spiraal overhouden. Met de omtrek van onze spiraal gedefinieerd, kan de Convert to Solid operatie worden gebruikt om een enkel geometrie object te maken. Deze 2D spiraal kan ten slotte worden geëxtrudeerd naar 3D met de Extrude functie.
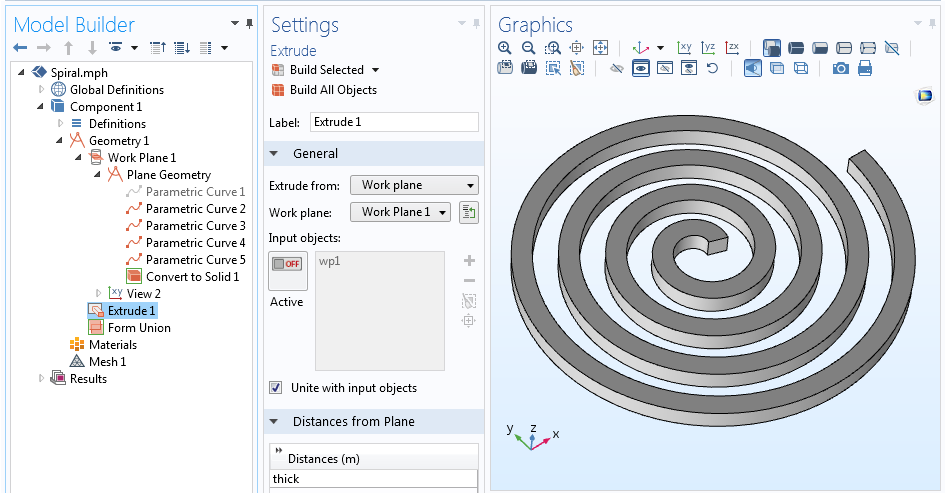
De volledige geometriesequentie en geëxtrudeerde 3D spiraalgeometrie.
Afsluitende opmerkingen over het modelleren van Archimedespiralen in COMSOL Multiphysics
We hebben u door de stappen geleid van het maken van een volledig geparametriseerde Archimedespiraal. Met deze spiraal geometrie kunt u alle parameters veranderen en experimenteren met verschillende ontwerpen, of ze zelfs gebruiken als parameters in een optimalisatiestudie. Wij moedigen u aan deze techniek in uw eigen modelleerprocessen te gebruiken, om de analyse van uw specifiek op een spiraal gebaseerd engineeringontwerp te bevorderen.