Introdução
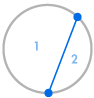
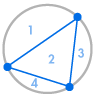
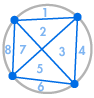
Imagine que colocamos vários pontos na circunferência de um círculo e ligamos todos os pontos uns com os outros. Isto divide o círculo em muitas regiões diferentes, e podemos contar o número de regiões em cada caso. Os diagramas abaixo mostram quantas regiões existem para vários números diferentes de pontos na circunferência. Temos de nos certificar que apenas duas linhas se encontram em cada intersecção dentro do círculo, e não três ou mais.
 |
 |
 |
 |
 |
| 1 região | 2 regiões | 4 regiões | 8 regiões | 16 regiões |
Podemos ver imediatamente um padrão: o número de regiões é sempre o dobro do anterior, de modo que obtemos a sequência 1, 2, 4, 8, 16, … Isto significa que com 6 pontos na circunferência haveria 32 regiões, e com 7 pontos haveria 64 regiões.
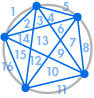
Poderíamos decidir que estamos felizes com este resultado. O número de regiões é sempre o dobro do anterior – depois de tudo isso funcionou para os primeiros cinco casos. Ou podemos decidir que devemos verificar mais alguns, só por segurança:
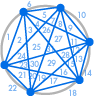 |

|
| 31 regiões, não 32 | 57 regiões, não 64 |
Felizmente algo deu errado: 31 pode parecer um erro de contagem, mas 57 é muito menos que 64. A sequência continua 99, 163, 256, …, muito diferente do que obteríamos ao duplicar o número anterior.
Este exemplo ilustra porque, em matemática, não se pode simplesmente dizer que uma observação é sempre verdadeira só porque funciona em alguns casos que você já testou. Em vez disso, você tem que inventar um argumento lógico rigoroso que leve dos resultados que você já conhece, a algo novo que você quer mostrar para ser verdade. Tal argumento é chamado de prova.
Provas são o que torna a matemática diferente de todas as outras ciências, porque uma vez provado algo, temos a certeza absoluta de que é e sempre será verdade. Não é apenas uma teoria que se encaixa em nossas observações e pode ser substituída por uma teoria melhor no futuro.
No exemplo acima, poderíamos contar o número de intersecções no interior do círculo. Pensando cuidadosamente sobre a relação entre o número de intersecções, linhas e regiões, eventualmente nos levará a uma equação diferente para o número de regiões quando há x = V.Pontos Axi no círculo:
Número de regiões = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Esta equação funciona em todos os casos acima. Poderíamos agora tentar provar para cada valor de x usando “indução”, uma técnica explicada abaixo.
Tradicionalmente, o fim de uma prova é indicado usando um ■ ou □, ou escrevendo QED ou “quod erat demonstrandum”, que é latim para “o que tinha que ser mostrado”.
Um resultado ou observação que pensamos ser verdadeiro é chamado de Hipótese ou Conjectura. Uma vez provado, nós o chamamos de Teorema. Uma vez provado um teorema, podemos usá-lo para provar outros resultados, mais complicados – construindo assim uma rede crescente de teoremas matemáticos.
Axiomas

Escola de Rafael de Atenas: os antigos matemáticos gregos foram os primeiros a abordar a matemática usando uma estrutura lógica e axiomática.
Uma questão interessante é por onde começar. Como provar o primeiro teorema, se você ainda não sabe nada? Infelizmente você não pode provar algo usando nada. Você precisa de pelo menos alguns blocos de construção para começar, e estes são chamados de Axiomas.
Os matemáticos assumem que os axiomas são verdadeiros sem serem capazes de os provar. Contudo, isto não é tão problemático como pode parecer, porque os axiomas ou são definições ou são claramente óbvios, e só existem muito poucos axiomas. Por exemplo, um axioma poderia ser que a + b = b + a para quaisquer dois números a e b.
Axiomas são importantes para se acertar, porque toda a matemática repousa sobre eles. Se houver muito poucos axiomas, você pode provar muito pouco e a matemática não seria muito interessante. Se houver demasiados axiomas, você pode provar quase tudo, e a matemática também não seria interessante. Também não pode ter axiomas que se contradigam.
A matemática não se trata de escolher o conjunto certo de axiomas, mas de desenvolver uma estrutura a partir destes pontos de partida. Se você começar com axiomas diferentes, você terá um tipo diferente de matemática, mas os argumentos lógicos serão os mesmos. Cada área da matemática tem o seu próprio conjunto de axiomas básicos.
Quando os matemáticos provaram um teorema, publicam-no para que outros matemáticos o verifiquem. Às vezes eles encontram um erro no argumento lógico, e às vezes um erro só é encontrado muitos anos depois. No entanto, em princípio, é sempre possível decompor uma prova nos axiomas básicos.
Conjunto Teoria e Axioma de Escolha

Para formular provas é por vezes necessário voltar ao próprio fundamento da linguagem em que a matemática é escrita: set theory.
Um conjunto é um conjunto de objectos, tais números. Os elementos de um conjunto são geralmente escritos entre parênteses curvilíneos. Podemos encontrar a união de dois conjuntos (o conjunto de elementos que estão em qualquer conjunto) ou podemos encontrar a intersecção de dois conjuntos (o conjunto de elementos que estão em ambos os conjuntos).
Muitos problemas matemáticos podem ser formulados na linguagem da teoria dos conjuntos, e para prová-los precisamos de axiomas da teoria dos conjuntos. Ao longo do tempo, os matemáticos têm utilizado várias coleções diferentes de axiomas, sendo os mais amplamente aceitos nove axiomas Zermelo-Fraenkel (ZF):
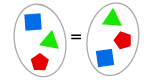
AXIOM DE EXTENSÃO
Se dois conjuntos têm os mesmos elementos, então eles são iguais.
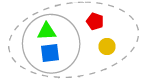
AXIOM DE SEPARAÇÃO
Podemos formar um subconjunto de um conjunto, que consiste em alguns elementos.

AXIOM DO CONJUNTO DE EMPRESAS
Existe um conjunto sem membros, escrito como {} ou ∅.
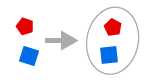
PAIR-SET AXIOM
Dados dois objectos x e y podemos formar um conjunto {x, y}.
UNION AXIOM
Podemos formar a união de dois ou mais conjuntos.
>
AXIOM DO CONJUNTO DE POTÊNCIA
Dando qualquer conjunto, podemos formar o conjunto de todos os subconjuntos (o conjunto de potência).
AXIOM DE INFINIDADE
Existe um conjunto com infinitos elementos.

EIXO DA FUNDAÇÃO
Os conjuntos são construídos a partir de conjuntos mais simples, o que significa que cada conjunto (não vazio) tem um membro mínimo.
AXIOM DE REPLACEMENTO
Se aplicarmos uma função a cada elemento de um conjunto, a resposta ainda é um conjunto.
Se pensarmos na teoria de conjuntos, a maioria destes axiomas parecerá completamente óbvia – e isto é o que se supõe que sejam os axiomas. Contudo existe um décimo axioma que é bastante mais problemático:
AXIOM OF CHOICE
Dados infinitamente muitos conjuntos não vazios, você pode escolher um elemento de cada um destes conjuntos.
À primeira vista, o Axioma da Escolha (AC) parece tão inocente quanto os outros acima. No entanto o uso do infinito tem uma série de consequências inesperadas. Por exemplo, você pode usar CA para provar que é possível cortar uma esfera em cinco pedaços e remontá-los para fazer duas esferas, cada uma idêntica à esfera inicial. Este é apenas um conceito teórico – os cortes necessários são fractais, o que significa que eles não podem realmente existir na vida real, e algumas das peças são “não mensuráveis”, o que significa que eles não têm um volume definido. Mas o facto de o Axioma da Escolha poder ser utilizado para construir estes cortes impossíveis é bastante preocupante.
Há um debate apaixonado entre os lógicos, se aceitam ou não o axioma da escolha. Cada coleção de axiomas forma um pequeno “mundo matemático”, e teoremas diferentes podem ser verdadeiros em mundos diferentes. É realmente apenas uma questão de se você está feliz por viver em um mundo onde você pode fazer duas esferas de um…
Proof by Induction
Proof by Induction é uma técnica que pode ser usada para provar que uma certa afirmação é verdadeira para todos os números naturais 1, 2, 3, … A “afirmação” é geralmente uma equação ou fórmula que inclui uma variável n que poderia ser qualquer número natural. Denotemos a afirmação aplicada a n por S(n). Aqui estão os quatro passos da indução matemática:
- Primeiro provamos que S(1) é verdadeiro, ou seja, que a declaração S é verdadeira para 1.
- Agora assumimos que S(k) é verdadeiro, ou seja, que a declaração S é verdadeira para algum número natural k.
- Usando esta suposição, tentamos deduzir que S(k + 1) também é verdadeiro. Assim sempre que S é verdadeiro para um número, também é verdadeiro para o próximo número.
- Desde que sabemos que S(1) é verdadeiro, S(2) deve ser verdadeiro. E portanto S(3) deve ser verdadeiro. E portanto S(4) tem que ser verdadeiro. E assim por diante: S tem de ser verdadeiro para todos os números.

Indução pode ser comparada a dominós em queda: sempre que um dominó cai, o próximo também cai. O primeiro passo, provando que S(1) é verdadeiro, inicia a infinita reação em cadeia.
O primeiro passo é muitas vezes negligenciado, porque é tão simples. Na verdade é muito importante e toda a cadeia de indução depende disso – como alguns dos exemplos a seguir mostrarão…
O objetivo do jogo Towers of Hanoi é mover um número de discos de uma cavilha para outra. Você só pode mover um disco de cada vez, e não é permitido colocar um disco maior em cima de um menor. Tente mover a torre de discos do primeiro pino para o último pino, com o menor número possível de movimentos:
Número de discos: Movimentos de Arranque: 0
Após termos entendido as regras do jogo, podemos tentar encontrar o menor número de passos necessários, dado qualquer número de discos. Jogar com o jogo acima pode nos levar a observar que, com n discos, você precisa de pelo menos 2n – 1 passos. Vamos chamar esta afirmação de S(n).
S(1) é claramente verdade pois, com apenas um disco, você só precisa de um movimento, e 21 – 1 = 1.
Agora vamos assumir que S(k) é verdade, ou seja, que você precisa de 2k – 1 passos para os discos k. Então se tivermos k + 1 discos:
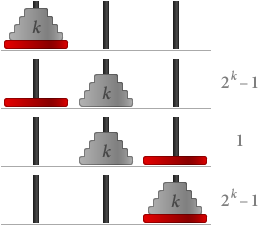
No total precisamos (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 passos. Isto significa que S(k + 1) também é verdadeiro.
Por indução matemática, S(n) é verdadeiro para todos os valores de n, o que significa que a forma mais eficiente de mover n = V.Hanoi discos leva 2n – 1 = Math.pow(2,V.Hanoi)-1 movimentos. ■
Deixe-nos usar indução para provar que a soma dos primeiros n números naturais é n (n + 1)2. Primeiro verificamos a equação para pequenos valores de n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Nextremo, assumimos que o resultado é verdadeiro para k, ou seja, que 1 + 2 + … + k = k (k + 1)2, onde k é algum número que não especificamos. Agora
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Acabamos de provar que se a equação é verdadeira para k, então também é verdadeira para k + 1. Por indução matemática, a equação é verdadeira para todos os valores de n. ■
Há outra forma inteligente de provar a equação acima, que não usa indução. Alegadamente, Carl Friedrich Gauss (1777 – 1855), um dos maiores matemáticos da história, descobriu este método na escola primária, quando seu professor lhe pediu para somar todos os números inteiros de 1 a 100.
Usando a indução, queremos provar que todos os seres humanos têm a mesma cor de cabelo. Que S(n) seja a afirmação de que “qualquer grupo de n seres humanos tem a mesma cor de cabelo”.
Claramente S(1) é verdade: em qualquer grupo de apenas um, todos têm a mesma cor de cabelo.
Agora assuma S(k), que em qualquer grupo de k todos têm a mesma cor de cabelo. Se substituirmos qualquer um do grupo por outro, eles ainda fazem um total de k e, portanto, têm a mesma cor de cabelo. Isto funciona para qualquer grupo inicial de pessoas, o que significa que qualquer grupo de k + 1 também tem a mesma cor de cabelo. Portanto S(k + 1) é verdadeiro.
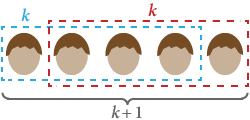
Por indução matemática, todos os seres humanos têm a mesma cor de cabelo! ■
Claramente algo deve ter corrido mal na prova acima – afinal de contas, nem todos têm a mesma cor de cabelo. Pode encontrar o erro?
Alguns teoremas não podem ser provados usando indução – temos de usar uma versão ligeiramente modificada chamada Indução Forte. Ao invés de assumirmos S(k) para provar S(k + 1), assumimos todos S(1), S(2), … S(k) para provar S(k + 1). Tudo que pode ser provado usando indução (fraca) também pode ser claramente provado usando indução forte, mas não vice-versa.
O Teorema Fundamental da Aritmética afirma que cada número inteiro maior que 1 ou é um número primo, ou pode ser escrito como o produto de números primos de uma forma essencialmente única.
Nós podemos provar partes dele usando forte indução: deixe S(n) ser a afirmação de que “o inteiro n é um número primo ou pode ser escrito como o produto de números primos”. S(1) é uma exceção, mas S(2) é claramente verdadeiro porque 2 é um número primo.
Agora vamos assumir que S(1), S(2), …, S(k) são todos verdadeiros, para alguns números inteiros k. Sabemos que k + 1 ou é um número primo ou tem fatores inferiores a k + 1. Pela nossa suposição, sabemos que estes factores podem ser escritos como o produto de números primos. Portanto, a menos que seja primo, k + 1 também pode ser escrito como um produto de números primos. Isto significa que S(k + 1) é verdadeiro.
Por forte indução, S(n) é verdadeiro para todos os números n maiores que 1. ■
Para provar que esta factorização principal é única (a menos que se conte diferentes ordenações dos factores) precisa de mais trabalho, mas não é particularmente difícil.
Verifica-se que o princípio da indução fraca e o princípio da indução forte são equivalentes: cada um implica o outro. Ambos também são equivalentes a um terceiro teorema, o Princípio do Bem-Emprego: qualquer conjunto (não vazio) de números naturais tem um elemento mínimo, menor que todos os outros.
O princípio do bem ordenado é a característica definidora dos números naturais. É um dos axiomas básicos utilizados para definir os números naturais ![]() = {1, 2, 3, …}. Estes axiomas são chamados de Axiomas Peano, nomeados em homenagem ao matemático italiano Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …}. Estes axiomas são chamados de Axiomas Peano, nomeados em homenagem ao matemático italiano Guiseppe Peano (1858 – 1932).
Proof by Contradiction
Proof by Contradiction é outra técnica de prova importante. Se quisermos provar uma afirmação S, assumimos que S não era verdade. Usando esta suposição, tentamos deduzir um resultado falso, tal como 0 = 1. Se todos os nossos passos estavam correctos e o resultado é falso, a nossa suposição inicial deve ter sido errada. Nossa suposição inicial era que S não é verdadeiro, o que significa que S é realmente verdadeiro.
Esta técnica pode ser usada em muitas circunstâncias diferentes, como provar que √2 é irracional, provar que os números reais são incontáveis, ou provar que existem infinitamente muitos números primos.
Aqui está outro exemplo divertido:
Podemos usar a prova por contradição, juntamente com o princípio do bem ordenado, para provar que todos os números naturais são “interessantes”.
Suponha que nem todos os números naturais são interessantes, e deixe S ser o conjunto de números não-interessantes. Pelo princípio de ordenação bem ordenada, S tem um menor membro x que é o menor número não-interessante. Esta propriedade curiosa claramente faz de x um número particularmente interessante. Isto é uma contradição porque assumimos que x era um número não-interessante.
Por isso todos os números são interessantes. ■
Gödel e Teoremas Improváveis

Kurt Gödel (1906-1978)
No início do século 20, a matemática começou a crescer rapidamente, com milhares de matemáticos trabalhando em inúmeras novas áreas. David Hilbert (1862 – 1943) criou um extenso programa para formalizar a matemática e resolver quaisquer inconsistências nos fundamentos da matemática. Isto incluiu provar todos os teoremas usando um conjunto de axiomas simples e universais, provar que este conjunto de axiomas é consistente e provar que este conjunto de axiomas é completo, ou seja, que qualquer afirmação matemática pode ser provada ou refutada usando os axiomas.
Felizmente, estes planos foram destruídos por Kurt Gödel em 1931. Ele provou que em qualquer sistema matemático (suficientemente complexo) com um determinado conjunto de axiomas, você pode encontrar algumas afirmações que não podem ser provadas nem refutadas usando esses axiomas. Também não é possível provar que um determinado conjunto de axiomas é consistente, utilizando apenas os próprios axiomas.
A descoberta de Gödel baseia-se no facto de um conjunto de axiomas não poder ser utilizado para dizer nada sobre si mesmo, como por exemplo, se é consistente. Os problemas de auto-referência não podem ser encontrados apenas na matemática, mas também na linguagem. Aqui está o Paradoxo Mentiroso:
“Esta frase é falsa”
A frase acima tenta dizer algo sobre si mesma. Se for verdade, então a frase diz-nos que é falsa. Se for falsa, então a frase nos diz que não é falsa, ou seja, que é verdadeira. Na verdade, a frase não é verdadeira nem falsa.
Quando publicada pela primeira vez, os teoremas de Gödel eram profundamente perturbadores para muitos matemáticos. Quando se trata de provar uma observação, não se sabe se existe uma prova – o resultado pode ser verdadeiro, mas não comprovável. Hoje sabemos que a incompletude é uma parte fundamental não só da lógica, mas também da informática, que se baseia em máquinas que realizam operações lógicas.
Surprendentemente, é possível provar que certas afirmações são impraticáveis. Um exemplo é a Hipótese do Continuum, que é do tamanho de conjuntos infinitos.
Para o fim da sua vida, Kurt Gödel desenvolveu graves problemas mentais e morreu de auto-esgana em 1978. Suas idéias sobre os fundamentos da lógica foram as mais profundas desde o desenvolvimento da prova pelos antigos gregos.