
Bertrand Russell (1872-1970) e A.N. Whitehead (1861-1947)
Bertrand Russell e Alfred North Whitehead eram matemáticos, lógicos e filósofos britânicos, que estavam na vanguarda da revolta britânica contra o idealismo continental no início do século XX e, entre eles, fizeram importantes contribuições nos campos da lógica matemática e da teoria dos conjuntos.
Whitehead era o mais velho dos dois e veio de uma formação matemática mais pura. Ele se tornou o tutor de Russell no Trinity College, Cambridge nos anos 1890, e então colaborou com seu ex-aluno mais célebre na primeira década do século 20 em seu monumental trabalho, o “Principia Mathematica”. Após a Primeira Guerra Mundial, porém, grande parte da qual Russell passou na prisão devido às suas atividades pacifistas, a colaboração foi mantida, e a carreira acadêmica de Whitehead permaneceu sempre à sombra da do mais flamboyant Russell. Ele emigrou para os Estados Unidos nos anos 20, e passou o resto de sua vida lá.
Russell nasceu em uma família rica da aristocracia britânica, embora seus pais fossem extremamente liberais e radicais para a época. Seus pais morreram quando Russell era bastante jovem e ele foi criado por sua avó vitoriana (embora bastante progressista). Sua adolescência foi muito solitária e ele sofria de crises de depressão, afirmando mais tarde que foi apenas seu amor pela matemática que o impediu de se suicidar. Ele estudou matemática e filosofia na Universidade de Cambridge sob G.E. Moore e A.N. Whitehead, onde se tornou um filósofo inovador, um prolífico escritor sobre muitos assuntos, um ateu comprometido e um matemático e lógico inspirado. Hoje, ele é considerado um dos fundadores da filosofia analítica, mas escreveu sobre quase todas as grandes áreas da filosofia, particularmente metafísica, ética, epistemologia, a filosofia da matemática e a filosofia da linguagem.
Russell foi um activista político empenhado e de alto perfil ao longo da sua longa vida. Foi um destacado activista anti-guerra durante a Primeira e Segunda Guerras Mundiais, defendeu o comércio livre e o anti-imperialismo e, mais tarde, tornou-se um forte defensor do desarmamento nuclear e do socialismo, e contra Adolf Hitler, o totalitarismo soviético e o envolvimento dos EUA na Guerra do Vietname.
Paradoxo de Russell
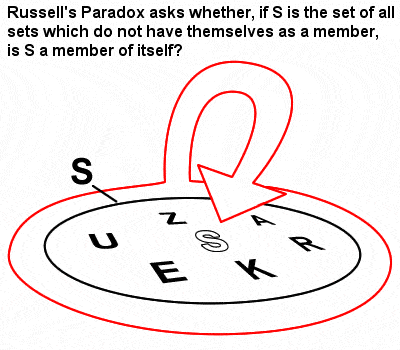
Paradoxo de Russell
A matemática de Russell foi grandemente influenciada pela teoria e lógica dos sets que Gottlob Frege tinha desenvolvido na sequência do trabalho pioneiro de Cantor nos sets. Em seu “The Principles of Mathematics” de 1903, porém, ele identificou o que ficou conhecido como o paradoxo de Russell (um conjunto contendo conjuntos que não são membros de si mesmos), o que mostrou que a teoria ingênua de Frege sobre conjuntos poderia de fato levar a contradições.
O paradoxo é às vezes ilustrado por este exemplo simplista: “Se um barbeiro barbeia todos e só aqueles homens da aldeia que não se barbeam a si próprios, será que se barbeia a si próprio?”
O paradoxo parecia implicar que os próprios fundamentos de toda a matemática já não podiam ser confiáveis, e que, mesmo na matemática, a verdade nunca poderia ser absolutamente conhecida (o trabalho posterior de Gödel e Turing só iria piorar isto). A crítica de Russell foi suficiente para abalar a confiança de Frege em todo o edifício do racionalismo, e ele foi gracioso o suficiente para admitir isso abertamente num apêndice apressadamente escrito ao Volume II de suas “Leis Básicas de Aritmética”.
Mas a magnum opus de Russell foi a monolítica “Principia Mathematica”, publicada em três volumes em 1910, 1912 e 1913. O primeiro volume foi co-escrito por Whitehead, embora os dois últimos tenham sido quase todos trabalhos de Russell. A aspiração desta ambiciosa obra foi nada menos que uma tentativa de derivar toda a matemática a partir de axiomas puramente lógicos, evitando os tipos de paradoxos e contradições encontrados no trabalho anterior de Frege sobre a teoria do conjunto. Russell conseguiu isso empregando uma teoria ou sistema de “tipos”, em que cada entidade matemática é atribuída a um tipo dentro de uma hierarquia de tipos, de modo que os objetos de um determinado tipo são construídos exclusivamente a partir de objetos de tipos anteriores mais baixos na hierarquia, evitando assim loops. Cada conjunto de elementos, portanto, é de um tipo diferente de cada um de seus elementos, de modo que não se pode falar do “conjunto de todos os conjuntos” e construções similares, o que leva a paradoxos.
No entanto, o “Principado” exigia, além dos axiomas básicos da teoria do tipo, mais três axiomas que pareciam não ser verdadeiros como meras questões de lógica, nomeadamente o “axioma do infinito” (que garante a existência de pelo menos um conjunto infinito, nomeadamente o conjunto de todos os números naturais), o “axioma da escolha” (que garante que, dado qualquer conjunto de “silos”, Cada um contendo pelo menos um objeto, é possível fazer uma seleção de exatamente um objeto de cada caixa, mesmo que haja infinitamente muitas caixas, e que não haja “regra” para qual objeto escolher de cada uma) e o próprio “axioma de reducibilidade” de Russell (que afirma que qualquer função de verdade proposicional pode ser expressa por uma função de verdade predicativa formalmente equivalente).
Durante os dez anos ou mais que Russell e Whitehead passaram no “Principia”, rascunho após rascunho foi iniciado e abandonado, pois Russell constantemente repensou suas premissas básicas. Russell e sua esposa Alys até se mudaram com os Whiteheads a fim de agilizar o trabalho, embora seu próprio casamento tenha sofrido à medida que Russell se apaixonou pela jovem esposa de Whitehead, Evelyn. Eventualmente, Whitehead insistiu na publicação da obra, mesmo que ela não estivesse (e talvez nunca estivesse) completa, embora eles fossem forçados a publicá-la às suas próprias custas, pois nenhuma editora comercial a tocaria.
Principia Mathematica

>
Uma pequena parte da longa prova de que 1+1 =2 no “Principia Mathematica”
Uma certa ideia do alcance e abrangência do “Principia” pode ser obtida a partir do fato de que são necessárias mais de 360 páginas para provar definitivamente que 1 + 1 = 2.
Hoje, é amplamente considerado como uma das obras mais importantes e seminais em lógica desde o “Organon” de Aristóteles. Pareceu notavelmente bem sucedida e resistente em seus ambiciosos objetivos, e logo ganhou fama mundial para Russell e Whitehead. De fato, foi apenas o teorema de Gödel de 1931 que finalmente mostrou que o “Principia” não poderia ser consistente e completo.
Russell recebeu a Ordem de Mérito em 1949 e o Prêmio Nobel de Literatura no ano seguinte. Sua fama continuou a crescer, mesmo fora dos círculos acadêmicos, e ele se tornou um nome familiar em vida posterior, embora em grande parte como resultado de suas contribuições filosóficas e de seu ativismo político e social, que ele continuou até o fim de sua longa vida. Ele morreu de influenza em seu amado País de Gales na grande velhice de 97,
| << De volta a Hardy e Ramanujan | Em frente a Hilbert >> |