16.3 Estratégias mistas
Objectivo de aprendizagem
- Que jogos requerem ou admitem aleatorização como parte da sua solução?
Deixe-nos considerar novamente o jogo dos cêntimos correspondentes, como ilustrado na Figura 16.13 “Centavos correspondentes novamente”.
Figure 16.13 Centavos correspondentes novamente
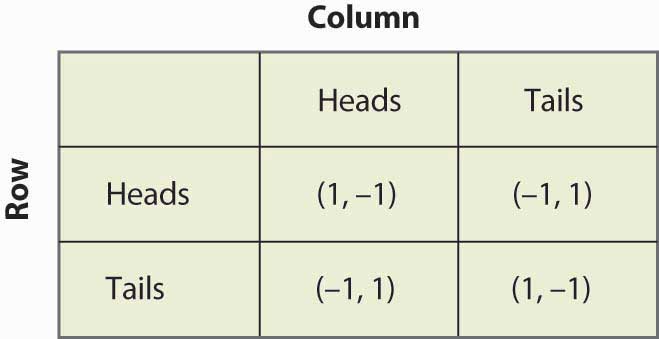
Suponha que Row acredita que a Coluna joga Heads com probabilidade p. Então se Row joga Heads, Row recebe 1 com probabilidade p e -1 com probabilidade (1 – p), para um valor esperado de 2p – 1. Da mesma forma, se a Linha jogar Cauda, a Linha recebe -1 com probabilidade p (quando a Coluna jogar Cabeças), e 1 com probabilidade (1 – p), para um valor esperado de 1 – 2p. Isto é resumido na Figura 16.14 “Estratégia mista em centavos iguais”.
Se 2p – 1 > 1 – 2p, então a linha é melhor, em média, jogando de cabeça do que de cauda. Da mesma forma, se 2p – 1 < 1 – 2p, então Row está melhor jogando Tails do que Tails. Se, por outro lado, 2p – 1 = 1 – 2p, então o Row recebe o mesmo pagamento não importa o que o Row faça. Neste caso, Row poderia jogar Heads, poderia jogar Tails, ou poderia virar uma moeda e aleatorizar o jogo de Row.
Uma estratégia mista Equilíbrio de NashUm equilíbrio de Nash em que pelo menos um jogador joga uma estratégia aleatória e nenhum jogador é capaz de aumentar seu payoff esperado jogando uma estratégia alternativa. envolve pelo menos um jogador jogando uma estratégia aleatória e nenhum jogador sendo capaz de aumentar seu payoff esperado jogando uma estratégia alternativa. Um equilíbrio de Nash em que nenhum jogador aleatoriza é chamado de estratégia pura Equilíbrio de NashUm equilíbrio de Nash em que nenhum jogador aleatoriza..
Figure 16.14 Estratégia mista em centavos iguais
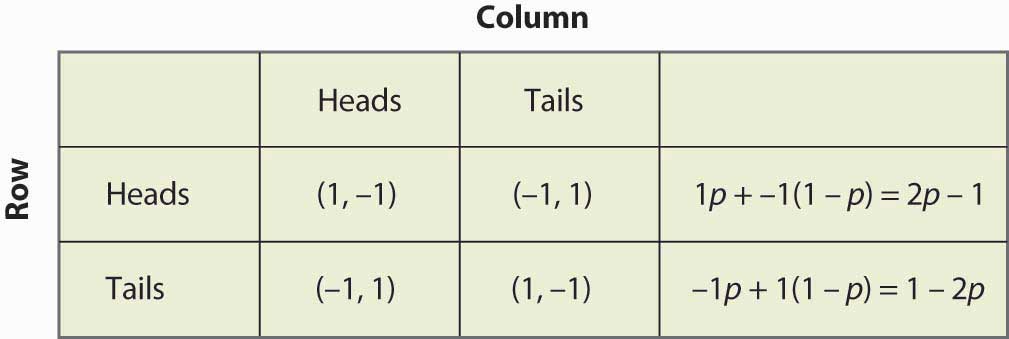
Nota que a randomização requer igualdade de payoffs esperados. Se um jogador deve randomizar sobre a estratégia A ou estratégia B, então ambas as estratégias devem produzir o mesmo payoff esperado. Caso contrário, o jogador preferiria uma delas e não jogaria a outra.
Computar uma estratégia mista tem um elemento que muitas vezes parece confuso. Suponha que o Row vai randomizar. Então os payoffs do Row devem ser iguais para todas as estratégias que o Row joga com probabilidade positiva. Mas que a igualdade nos payoffs do Row não determina as probabilidades com as quais o Row joga nas várias linhas. Em vez disso, essa igualdade nos payoffs do Row irá determinar as probabilidades com as quais a Coluna joga nas várias colunas. A razão é que são as probabilidades da Coluna que determinam os payoffs esperados para a Linha; se a Linha vai aleatorizar, então as probabilidades da Coluna devem ser tais que a Linha está disposta a aleatorizar.
Assim, por exemplo, calculamos o payoff para a Linha de jogar Heads, que era 2p – 1, onde p era a probabilidade de que a Coluna jogasse Heads. Da mesma forma, o payoff para Row de jogar Tails foi de 1 – 2p. Row está disposta a randomizar se estes forem iguais, o que resolve para p = ½.
Agora vamos tentar um exemplo um pouco mais desafiador e revisitar a batalha dos sexos. Figura 16.15 “Estratégia mista na batalha dos sexos” ilustra mais uma vez os payoffs.
Figure 16.15 Estratégia mista na batalha dos sexos
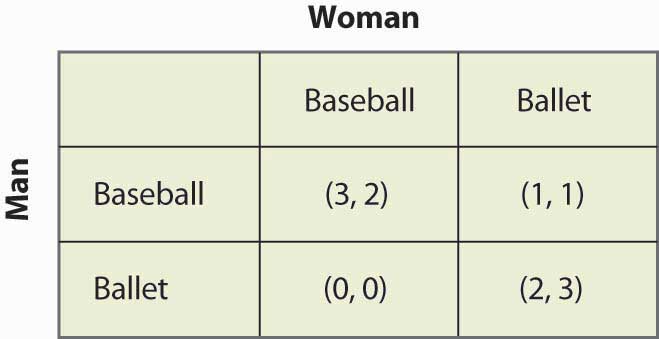
Este jogo tem dois equilíbrios de Nash de estratégia pura: (Basebol, Basebol) e (Ballet, Ballet). Existe uma estratégia mista? Para calcular uma estratégia mista, deixe a Mulher ir ao jogo de baseball com probabilidade p, e o Homem ir ao jogo de baseball com probabilidade q. Figura 16.16 “Cálculo completo da estratégia mista” contém o cálculo dos payoffs da estratégia mista para cada jogador.
Figure 16.16 Cálculo completo da estratégia mista
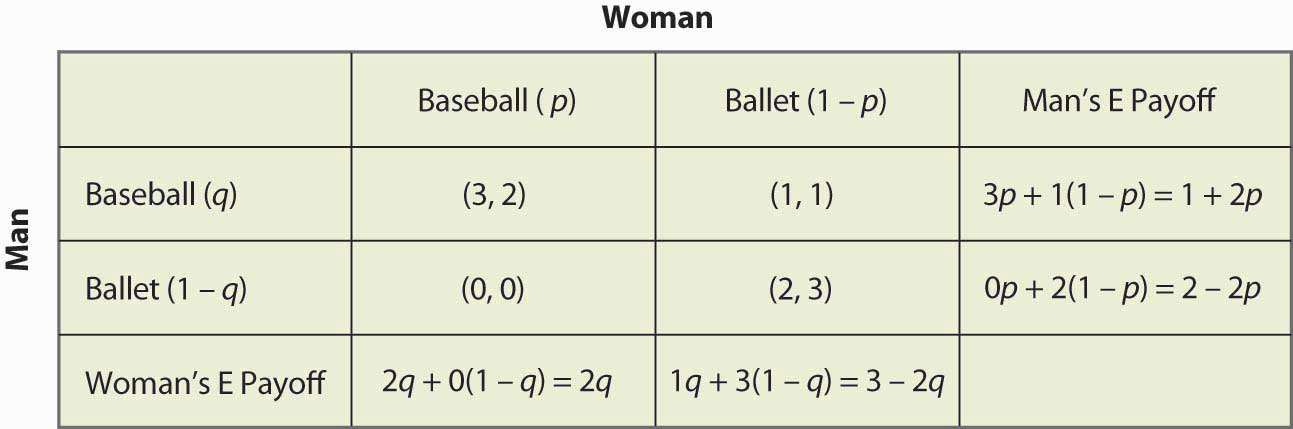
Por exemplo, se o Homem (jogador de linha) vai ao jogo de Baseball, ele recebe 3 quando a Mulher vai ao jogo de Baseball (probabilidade p), e caso contrário recebe 1, para um pagamento esperado de 3p + 1(1 – p) = 1 + 2p. Os outros cálculos são semelhantes, mas você definitivamente deve correr pela lógica e verificar cada cálculo.
Uma estratégia mista na batalha do jogo dos sexos requer que ambas as partes aleatorizem (já que uma estratégia pura de uma das partes impede a aleatorização pela outra). A indiferença do Homem entre ir ao jogo de Baseball e ao Ballet requer 1 + 2p = 2 – 2p, o que rende p = ¼. Ou seja, o Homem estará disposto a aleatorizar qual o evento que vai assistir se a Mulher for ao Ballet ¾ da época, e caso contrário ao jogo de Baseball. Isto torna o Homem indiferente entre os dois eventos porque prefere estar com a Mulher, mas também gosta de estar no jogo de Baseball. Para compensar a vantagem que o jogo tem para ele, a Mulher tem que estar no Ballet mais vezes.
Simplesmente, para que a Mulher aleatorize, a Mulher tem que receber pagamentos iguais de ir ao jogo de Baseball e ir ao Ballet, que requer 2q = 3 – 2q, ou q = ¾. Assim, a probabilidade do Homem ir ao jogo de Baseball é ¾, e ele vai ao Ballet ¼ da época. Estas são probabilidades independentes, pelo que para obter a probabilidade de ambos irem ao jogo de Basebol, multiplicamos as probabilidades, o que rende 3/16. Figura 16.17 “Probabilidades de estratégia mista” preenche as probabilidades para os quatro resultados possíveis.
Figure 16.17 Probabilidades de estratégia mista
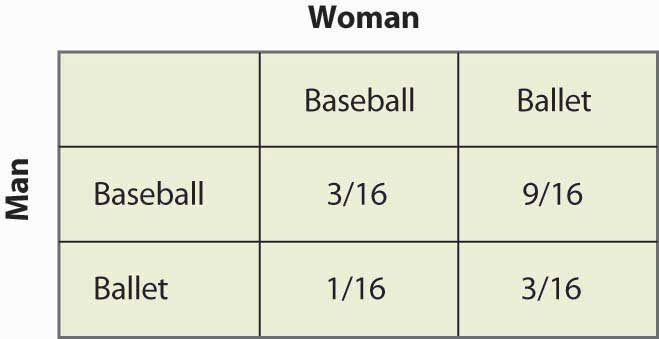
Notem que mais da metade do tempo (Baseball, Ballet) é o resultado da estratégia mista e as duas pessoas não estão juntas. Esta falta de coordenação é geralmente uma característica dos equilíbrios da estratégia mista. Os payoffs esperados para ambos os jogadores são prontamente computados também. O pagamento do Homem é de 1 + 2p = 2 – 2p, e desde p = ¼, o Homem obtém 1½. Um cálculo semelhante mostra que o payoff da Mulher é o mesmo. Assim, ambos fazem pior do que coordenar o seu resultado menos preferido. Mas este equilíbrio de Nash de estratégia mista, por indesejável que possa parecer, é um equilíbrio de Nash no sentido de que nenhuma das partes pode melhorar o seu próprio payoff, dado o comportamento da outra parte.
Na batalha dos sexos, o equilíbrio de Nash de estratégia mista pode parecer improvável; e podemos esperar que o casal coordene de forma mais eficaz. Na verdade, uma simples chamada ao telefone deve descartar a estratégia mista. Assim, vamos considerar outro jogo relacionado com a batalha dos sexos, onde uma falha de coordenação faz mais sentido. Este é o jogo da “galinha”. Neste jogo, dois jogadores dirigem-se um para o outro, tentando convencer o outro a ceder e acabando por se desviar para uma vala. Se ambos se desviarem para a vala, chamamos ao resultado um empate e ambos ficam a zero. Se um desviar e o outro não, o condutor que desviar perde e o outro condutor ganha, e daremos um ponto ao vencedor. Note que adicionar uma constante aos payoffs de um jogador, ou multiplicar os payoffs desse jogador por uma constante positiva, não afecta os equilíbrios de Nash – puro ou misto. Portanto, podemos sempre deixar que um resultado para cada jogador seja zero, e outro resultado seja um. A única questão que resta é o que acontece quando nenhum dos dois se rende, e nesse caso o resultado é um crash. Nesta versão, o payoff foi definido em quatro vezes a perda de swerving, como mostrado na Figura 16.18 “Galinha”, mas você pode mudar o jogo e ver o que acontece.
Figure 16.18 Chicken
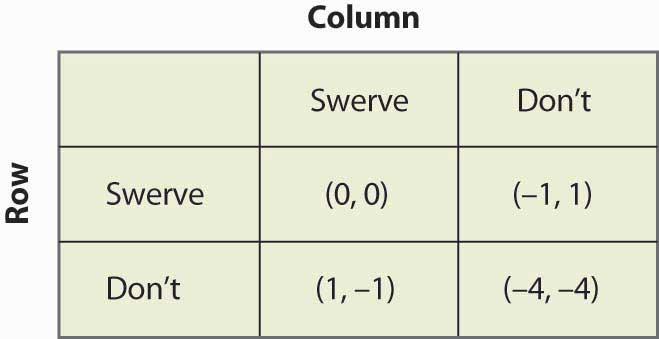
Este jogo tem dois equilíbrios de estratégia pura: (Swerve, Don’t) e (Don’t, Swerve). Além disso, ele tem uma estratégia mista. Suponha que a Coluna gira com probabilidade p. Então Row recebe 0p + -1(1 – p) de swerving, 1p + (-4)(1 – p) de não swerving, e Row irá randomizar se estes forem iguais, o que requer p = ¾. Ou seja, a probabilidade de a Coluna desviar em um equilíbrio de estratégia mista é ¾. Você pode verificar se o jogador da linha tem a mesma probabilidade definindo a probabilidade de que a linha gira igual a q e calculando os payoffs esperados da Coluna. Assim, a probabilidade de uma colisão é 1/16 no equilíbrio da estratégia mista.
O equilíbrio da estratégia mista é mais provável, em algum sentido, neste jogo: Se os jogadores já soubessem quem ia ceder, não precisariam realmente de jogar o jogo. O objectivo do jogo é descobrir quem vai ceder, o que significa que não se sabe antecipadamente quem vai ceder. Isto significa que o equilíbrio da estratégia mista é, em certo sentido, o equilíbrio mais razoável.
Figure 16.19 Rock, paper, scissors
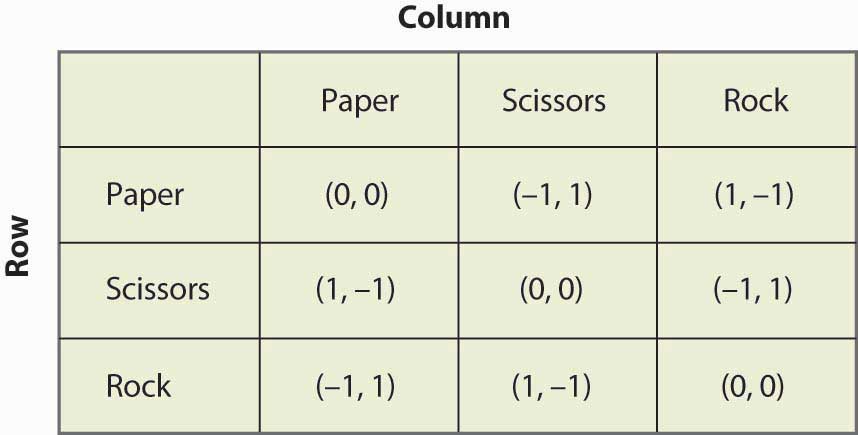
“Rock, paper, scissors” é um jogo infantil no qual duas crianças usam as mãos para simultaneamente escolherem papel (de mão segura), tesoura (mão com dois dedos salientes para parecerem tesouras), ou pedra (mão num punho). A natureza dos payoffs é que o papel bate a pedra, a pedra bate a tesoura, e a tesoura bate o papel. Este jogo tem a estrutura que é ilustrada na Figura 16.19 “Pedra, papel, tesoura”.
Key Takeaways
- Uma estratégia mista O equilíbrio de Nash envolve pelo menos um jogador jogando uma estratégia aleatória e nenhum jogador sendo capaz de aumentar seu payoff esperado jogando uma estratégia alternativa.
- Um equilíbrio de Nash sem randomização é chamado de equilíbrio de Nash de estratégia pura.
- Se um jogador é suposto randomizar mais de duas estratégias, então ambas devem produzir o mesmo payoff esperado.
- O jogo dos centavos correspondentes tem uma estratégia mista e nenhuma estratégia pura.
- O jogo dos sexos tem uma estratégia mista e duas estratégias puras.
- O jogo da galinha é semelhante à batalha dos sexos e, como ele, tem duas estratégias puras e uma estratégia mista.
Exercícios
- Deixe q seja a probabilidade de Row jogar Heads. Mostrar que a Coluna está disposta a randomizar, se e somente se q = ½. (Dica: Primeiro calcule o payoff esperado da Coluna quando a Coluna jogar Heads, e depois calcule o payoff esperado da Coluna quando a Coluna jogar Tails. Estes devem ser iguais para que a Coluna randomize.)
- Mostrar que no jogo de pedra, papel, tesoura, não há puro equilíbrio de estratégia. Mostre que jogar as três ações com a mesma probabilidade é um equilíbrio de estratégia mista.
-
Conheça todos os equilíbrios dos seguintes jogos:
Figure 16.20
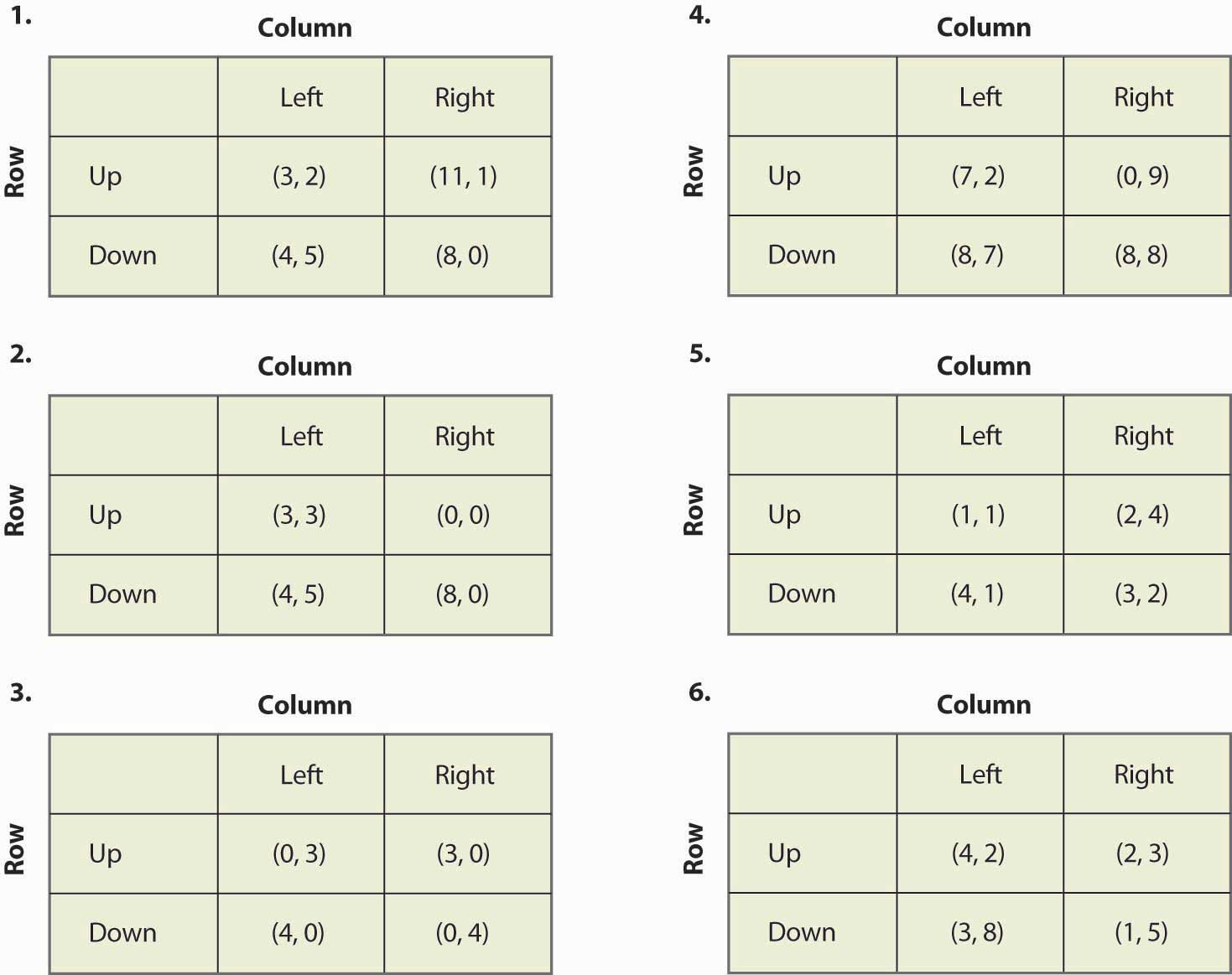
- Se você multiplicar o payoff de um jogador por uma constante positiva, os equilíbrios do jogo não mudam. Isto é verdade ou falso, e porquê?